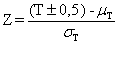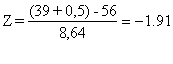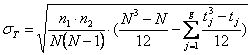METODI NON PARAMETRICI PER DUE CAMPIONI INDIPENDENTI

 

 

 

9.6.   Il test di Wilcoxon-Mann-Whitney della somma dei ranghi

 

 

Nel test della mediana un dato fornisce lo stesso contributo al calcolo della significatività quando, collocato dalla stessa parte, è prossimo alla mediana oppure se ne discosta sensibilmente. Anche da questa osservazione elementare, è semplice dedurre che quel test utilizza solamente una parte minima dell'informazione contenuta nelle due serie di dati.

Tra vari test che utilizzano appieno l'informazione del rango (tuttavia ancora inferiore a quella di una scala a intervalli o di rapporti), nel caso di due campioni indipendenti i più noti sono:

-          il test di Wilcoxon-Mann-Whitney (a volte abbreviato in WMW test) o test della somma dei ranghi,

-           il test U di Mann-Whitney, detto anche test dell'ordine robusto dei ranghi, che usa una procedura leggermente differente, non ancora presentata nel testo e fondata sulle precedenze

-          il test S di Kendall che elabora diversamente l’indicatore di Mann-Whitney.

 

Il test della somma dei ranghi è stato originariamente proposto da F. Wilcoxon nel 1945 (vedi Individual comparisons by ranking method, in Biometrics, Vol. 1, pp. 80-83). In vari testi è quindi chiamato semplicemente test di Wilcoxon per 2 campioni indipendenti. In questa prima versione aveva il grave limite di poter essere applicato solo a due campioni indipendenti, di dimensioni uguali.

La sua applicazione è stata generalizzata e estesa anche al caso di 2 campioni con un numero differente di repliche da H. B. Mann e D. R. Whitney nel 1947, diventando il metodo di Wilcoxon-Mann-Whitney. Questi due ultimi autori hanno avuto il merito ulteriore di proporre un metodo nuovo (vedi On a test of whether one of two random varaibles is stochastically larger than the other, pubblicato su Annals of Mathematical Statistics, Vol. 18, pp. 50-60), fondato su una logica differente dal conteggio dei ranghi.

Il test di Wilcoxon è stato descritto anche da W. H. Kruskal nel 1957 (vedi Historical notes on the Wilcoxon unpaired two-sample test, pubblicato da Journal of the American Statistical Association, Vol. 52, pp. 356-360).

Attualmente, in molti testi viene presentata solamente la versione di Mann-Whitney. In questo corso sono presentati entrambi, allo scopo di mostrare come siano possibili due metodologie differenti, per risolvere lo stesso problema:

-          la prima fondata sui ranghi,

-          la seconda sulle precedenze

 e si possano trasferire i risultati di uno all’altro.

 

Il metodo di Wilcoxon-Mann-Whitney (WMW test) richiede che

-          le due popolazioni a confronto siano distribuite in modo continuo,

-          abbiano la stessa forma rispetto alla simmetria (entrambe simmetriche o entrambe asimmetriche nello stesso modo) e che

-          i dati siano misurati con una scala almeno ordinale.

Le ipotesi possono essere

-          bilaterali

      contro     

 

-          unilaterali in una direzione

      contro     

  oppure nell’altra

     contro    

e dove

-           sono rispettivamente la mediana del gruppo 1 e la mediana del gruppo 2.

 

(Si ripropone l'esercizio già utilizzato con il test della mediana, per un confronto tra i risultati e una valutazione della potenza dei due test.)

Nel centro storico di una città, per l'analisi della qualità dell'aria sono state rilevate le quantità di solventi aromatici (Benzene, Toluene, Etilbenzene, Xileni in microgrammi/mc) presenti in un giorno festivo ed in un giorno feriale.

 

 

 

Con i dati della tabella, verificare se nel giorno festivo la quantità di solventi aromatici è significativamente minore di quella presente nel giorno feriale.

La metodologia può essere scomposta nei suoi passaggi logici:

 

1 - Combinare i dati dei due gruppi in una serie unica, disponendo i valori o punteggi in ordine crescente. Per questo ordinamento in ranghi, quando esistono dati negativi si utilizzano i valori algebrici: si assegnano i ranghi minori ai valori negativi che sono maggiori in modulo.

 

Per ogni dato, conservare l'informazione relativa al gruppo di appartenenza, come nella tabella seguente:

 

 

 

2 - Definire

-           la dimensione del gruppo minore,

-           la dimensione del gruppo maggiore.

Se i 2 gruppi hanno la stessa dimensione, l'attribuzione di  e  può essere casuale, in quanto indifferente sui risultati.

 Nell’esempio,   = 7   e    = 8.

 

Attribuire il rango ad ogni valore nella serie unita dei due campioni.

 

 

 

3 - Calcolare la somma dei ranghi (chiamata T oppure W) del gruppo con il numero di dati minore.

Nell’esempio, è il gruppo A: il numero di repliche è indicato con  (i suoi ranghi sono stati riportati nella tabella precedente in grassetto e sottolineati).

 

La somma di questi  ranghi

 risulta T = 39.

 

4 - Quando l'ipotesi nulla H₀ è vera, i valori del gruppo prescelto sono casualmente mescolati con quelli dell’altro gruppo. Di conseguenza, il valore di T tende ad una media attesa m_T, che dipende dal numero di osservazioni ( e  )  dei 2 gruppi, secondo la relazione

 

 

Con i dati dell'esempio ( = 7   e    = 8)

 

 la media attesa è m_T = 56.

 

5 - Se l’ipotesi nulla H₀ è falsa e quindi è vera l'ipotesi alternativa H₁, il valore di T osservato tende ad essere maggiore o minore di questo valore atteso (m_T), in rapporto alla coda della distribuzione nella quale è collocata la tendenza centrale del gruppo con meno dati.

Di conseguenza, il valore di T può tendere verso uno dei due estremi:

-          un valore minimo, dato dalla somma degli  ranghi minori,

-          un valore massimo, determinato dalla somma degli  ranghi maggiori.

 

6 - La significatività della differenza tra le mediane dei due gruppi può essere valutata confrontando il valore di T calcolato con il valore m_T atteso.

 

Nel caso di piccoli campioni ( e   £ 10), i valori critici alla probabilità a = 0.05 sono forniti dalla tabella  per un test unilaterale (quelli per un test bilaterale non sono stati riportati, perché non trovati in nessun testo consultato).

Per ogni coppia  ed  la tabella riporta la probabilità di trovare il valore di T osservato o valori che si discostano maggiormente dalla media

-          nella coda inferiore e

-          in quella superiore della distribuzione.

 

 

Tavola dei valori critici di T del test di Wilcoxon-Mann-Whitney

per test unilaterali con 2 campioni indipendenti

 Probabilità a £ 0.05

 

-           = campione con il numero minore di osservazioni,

-           = campione con il numero maggiore di osservazioni,

-          T è significativo quando è uguale o minore del valore minore tabulato,

-          T è significativo quando è uguale o maggiore del valore maggiore tabulato

 

 

 

 

 

 

 

Tavola dei valori critici di T del test di Wilcoxon-Mann-Whitney

per test bilaterali con 2 campioni indipendenti

 Probabilità a £ 0.05 nella  parte superiore

 Probabilità a £ 0.01 nella parte inferiore

 

-           = campione con il numero minore di osservazioni,

-           = campione con il numero maggiore di osservazioni,

-          T è significativo quando è uguale o minore del valore tabulato,

 

 

Con i dati dell'esempio, per  = 7   e    = 8   la media attesa è 56 mentre il valore T calcolato è 39. Si tratta quindi di verificare se è minore dell’atteso in modo significativo.

Il valore critico fornito dalla tabella per   = 7   e   = 8   è   T = 41.

Il valore osservato (39) è inferiore a quello critico riportato nella tabella (41): di conseguenza, la probabilità (P) che possa essere ottenuto per caso è inferiore a 0.05.

Per questo test ad una coda, si rifiuta l'ipotesi nulla.

 

E’ utile osservare come questo test sia molto più potente di quello della mediana: con gli stessi dati,

-          il test della mediana stimava una probabilità P = 0.21445,

-          il test di Wilcoxon-Mann-Whitney stima P < 0.05 (in modo approssimato, con l’uso della tabella). La stima successiva, ottenuta con la normale benché il campione sia piccolo e quindi sottostimata, fornisce un probabilità P @ 0.03.

 

 

Nel caso di grandi campioni ( oppure  > 10) la statistica T segue una distribuzione approssimativamente normale. La significatività può pertanto essere saggiata mediante la distribuzione normale ridotta, con media uguale a 0 e varianza uguale a 1.

Anche quando in un gruppo si hanno più di 10 osservazioni, è conveniente applicare la correzione per la continuità, sommando ± 0,5 al valore di T, in modo che lo scarto tra osservato ed atteso sia più piccolo.

La formula della stima di Z, corretta per la continuità,

 diviene

 dove la media m_T è data da

 e la deviazione standard _ da

Con i dati dell'esempio,

 dove m_T è uguale a 56

 e la deviazione standard _ è

 uguale a 8,64

 la significatività della differenza tra le due tendenze centrali può essere verificata attraverso il valore di Z

 che risulta uguale a -1,91.

Il segno indica che il valore osservato è inferiore a quello atteso; al valore di 1,91 in una coda della distribuzione nella tabella della distribuzione normale corrisponde un'area di probabilità P = 0.0281.

Si rifiuta l'ipotesi nulla.

 

Quando i punteggi non sono valutati con una scala continua, come postula il test, si possono avere diversi valori uguali od osservazioni ex-aequo (ties). Nella trasformazione in ranghi, ad ognuna di queste osservazioni viene assegnata la media dei ranghi dei valori uguali. La media resta invariata, ma la deviazione standard _  è minore; di conseguenza deve essere corretta e

 diventa

 

 

 dove

-           e la stima dei t è condotta come nel test T di Wilcoxon per 2 campioni dipendenti.

 

La correzione per i ties diminuisce il valore della deviazione standard e quindi aumenta il valore di Z.

 

 

ESEMPIO 1.   Quantità di precipitazione, intensità e durata delle piogge variano da luogo a luogo. L’irregolarità degli eventi atmosferici e una diversa configurazione sia del suolo che di aspetti ambientali (zone montuose, aree alberate od urbanizzate) possono influire sulla quantità di pioggia. Tuttavia è ritenuto approssimativamente corretto considerare valide per tutta l’area le misure effettuate in una stazione pluviometrica.

Per verificare se un’area montana (M) ha avuto una quantità di piogge significativamente superiore a quella di un’area collinare (C) limitrofa, sono state raccolte le due brevi serie mensili (in millimetri), non coincidenti come periodo.

 

 

Risposta.

E’ un test ad una coda, con le seguenti ipotesi sulle mediane

H₀: Me_M £ Me_C      contro      H₁: Me_M > Me_C

 

Per effettuare il test, la procedura richiede i passaggi seguenti.

 

1 - Ordinare i valori, conservando l’informazione del gruppo d’appartenenza; successivamente riportare i ranghi relativi.

 

 

 

2  - Calcolare la somma dei ranghi del gruppo M (già riportati in grassetto), con  = 4   e    = 6

T = 5 + 7 + 9 + 10 = 31

 

3 - Se H₀ fosse vera, il valore atteso di m_T dovrebbe essere

 

m_T =  =  = 22

 uguale a 22.

Il valore osservato (31) è più alto di quello atteso; pertanto il confronto deve essere condotto con il valore critico superiore.

Nella tabella dei valori critici, per  = 4  e  = 6 il valore massimo riportato è 31.

Il valore di T calcolato è esattamente uguale (31).

Poiché il valore riportato nella tabella appartiene all’area di rifiuto, si rifiuta l’ipotesi nulla e si accetta l’ipotesi alternativa.

La mediana delle quantità mensili di pioggia caduta nella zona montuosa è significativamente superiore alla mediana delle quantità mensili cadute in collina.

 

 

In vari testi di statistica applicata, non sono riportati i valori critici del test T o W di Wilcoxon-Mann-Whitney. In tali condizioni, si ricorre a quelli di Mann-Whitney dopo trasformazione del T in U, come sarà illustrato nei paragrafi successivi.

Come ultimo esempio di applicazione di questo test WMW, sono riportati dati tratti dal testo di Sprent, ma sviluppati in modo più dettagliato,

-          sia per una prima illustrazione del passaggio dai valori critici del test WMW a quelli di Mann-Whitney,

-          sia per riportare un esempio classico, che in seguito servirà per confrontare i risultati di test differenti applicati agli stessi dati.

 

ESEMPIO 2. (Uguale a quello già utilizzato per l’intervallo di confidenza con il test della mediana; sarà utilizzato anche in test successivi).

Si assuma di aver effettuato il conteggio di popolazioni batteriche in campioni d’acqua di due aree (10 pozzi dell’area A e 12 pozzi di quella B). I dati, riportati nella tabella, sono già stati ordinati per rango allo scopo di facilitarne la lettura e il confronto:

 

 

 

Esiste una differenza significativa tra le due tendenze centrali?

 

Risposta.

E’ un test bilaterale, con

      contro     

 

1 - Come primo passo, con  = 10    e    = 12,

 si ordinano i dati per rango come se appartenessero ad un gruppo unico, mantenendo l’informazione su quello di appartenenza; con i 22 dati campionari, si ottiene la seguente serie

 

 

 

 

 

2 - Dalla distribuzione congiunta, si ricavano i totali dei ranghi

-          del gruppo A (S_A)

S_A = 2 + 4 + 8 + 9+ 10 + 11 + 12 + 14 + 21 + 22 = 113

-          del gruppo B (S_B)

S_B = 1 + 3 + 5 + 6 + 7 + 13 + 15 + 16 + 17 + 18 + 19 + 20 = 140

Nel caso di campioni piccoli, si utilizza la tabella già riportata.

Ma in questo caso, con = 12 (campione più grande di quello massimo riportato nella tabella) e per un test bilaterale, si può ricorrere alla tabella del test U riportata nel paragrafo successivo.

La trasformazione del T in U è

 ricavata da

U = T -

Con i dati dell’esempio,

 da T = 113 si ricava

U = 113 -

 U = 58.

Il valore calcolato (58) supera quello massimo riportato nella tabella dei valori critici di U alla probabilità a = 0.05 in un test bilaterale e per le dimensioni  = 10    e    = 12: non è possibile rifiutare l’ipotesi nulla.

 

Trasformare il valore di T (o W) del test di WMW nel corrispondente valore U del test Mann-Whitney è prassi diffusa, riportata in molti testi. Sarà illustrata in modo più dettagliato in un paragrafo seguente. Purtroppo, vari testi presentano il test di Mann-Whitney in modo non corretto o almeno incompleto: calcolano i ranghi e trasformano la somma minore (T) nel valore corrispondente del test U, senza spiegare il modo con il quale U dovrebbe essere calcolato e quale sia il suo reale significato.