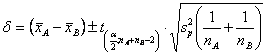METODI NON PARAMETRICI PER DUE CAMPIONI INDIPENDENTI

 

 

 

9.5. L’INTERVALLO DI CONFIDENZA PER UNA DIFFERENZA MEDIANA, CON IL METODO ESATTO DI FISHER.

 

 

Nell’analisi sulla qualità delle acque, è frequente il conteggio di popolazioni planctoniche o batteriche, che hanno una crescita esponenziale. La distribuzione di questi dati è fortemente asimmetrica; per l’applicazione di test parametrici sulla media, quale il test t di Student spiegato in precedenza, si deve preventivamente ricorrere alla trasformazione logaritmica, come sarà illustrato nel capitolo dedicato alle trasformazioni. Tuttavia, non sempre il risultato richiesto per la validità del test (la normalità della distribuzione e la omogeneità della varianza) è raggiunto in modo soddisfacente.

Il ricorso al test della mediana permette di ottenere inferenze difficilmente confutabili, anche in queste situazioni sperimentali che si allontanano dal modello richiesto per l’applicazione di un test parametrico.

 

Oltre all’inferenza sulla significatività della differenza, spesso è richiesta anche la stima di un suo valore medio o mediano, con il suo intervallo di confidenza. Il test della mediana si presta al calcolo di una stima non confutabile della differenza (d) vera

In alcuni casi di forte asimmetria, questo metodo risulta più potente di quello che utilizza la distribuzione t di Student.

 

Sviluppando l’esempio riportato nel testo di Sprent già citato (pag. 107-8), si assuma di aver effettuato il conteggio di popolazioni batteriche in campioni d’acqua di due aree (10 pozzi dell’area A e 12 pozzi di quella B), con i risultati della tabella, nella quale sono già stati ordinati per rango allo scopo di facilitarne la lettura e il confronto:

 

 

Determinare l’intervallo di confidenza alla probabilità nominale del 95% per la differenza tra le due mediane, utilizzando il metodo esatto di Fisher (Fisher’s exact test).

 

Risposta.   La procedura del test della mediana con campioni piccoli, cioè con il metodo esatto di Fisher,

 

1 - come primo passo richiede che i dati dei due campioni indipendenti siano disposti in ordine crescente, come se fossero un gruppo solo, mantenendo l’informazione sul gruppo di appartenenza; con i 22 dati campionari, si ottiene la seguente serie

 

 

 

 

 

 

 nella quale la mediana del gruppo riunito cade tra il rango 11 (287) e il rango 12 (291).

 

 

2 – Con pochi dati, la mediana è la media di questi due valori: 289.

Successivamente si costruisce la tabella 2 x 2,

 

 

nella quale emerge che

-          dei 10 dati del gruppo A, 6 sono inferiori e 4 sono maggiori della mediana comune,

-          dei 12 dati del gruppo B, 5 sono inferiori e 7 sono maggiori della mediana comune.

 

 

3 – Per stimare l’intervallo di confidenza alla probabilità bilaterale a = 0.05 è necessario calcolare quali sono le distribuzioni di frequenza che, mantenendo costanti i totali (di riga, di colonna e quindi  anche quello generale) della tabella, abbiano una probabilità (P) complessiva inferiore a a = 0.025 in ognuna delle due code della distribuzione.

Con un programma informatico, poiché i conti manuali sono lunghi seppure ancora possibili, si stima che

-          la probabilità (P₀) di ottenere la tabella seguente (la più estrema in una direzione)

 

 

 

 

 cioè la probabilità di avere 0 nella casella in alto a destra (ma 0 potrebbe anche essere in alto a sinistra, trattandosi di una distribuzione simmetrica)

è

0,000017

 approssimativamente uguale a 0.000;

-          la probabilità (P₁) di ottenere la tabella seguente

 

 

 

 

 cioè di avere 1 nella casella in alto a destra

 è

0,000936

 approssimativamente uguale a 0.001;

-          la probabilità (P₂) di ottenere la tabella

 

 

 

 

 cioè di avere 2 nella casella in alto a destra

 è

0,01403

 approssimativamente uguale a 0.014.

La probabilità (P₃) di avere 3, sempre solamente per effetto del caso,

è

0,08420

 

Questa ultima è alta (P₃ = 0.084), superando da sola il 5%.

 

4 – Da questi calcoli si deduce che

P = 0.000 + 0.001 +0.014 @ 0.015

 la probabilità complessiva di avere per solo effetto del caso le tre risposte più estreme in una coda è approssimativamente P = 0.015.

 

5 – Di conseguenza, per calcolare l’intervallo di confidenza alla probabilità complessiva a £ 0.05 considerando entrambe le code della distribuzione, il valore limite accettabile nel gruppo A è 303

 

 

 

 

 in quanto esclude solo i due valori più estremi: esso è il primo che non permette di rifiutare l’ipotesi nulla H₀.

 

6 – Successivamente si prendono in considerazione i dati del campione B. Poiché il numero totale di valori oltre la mediana sono 11, come riportano le tabelle 2 x 2 e sempre per non rifiutare l’ipotesi nulla H₀, nel gruppo B i valori che si possono escludere sono gli 8 maggiori. Nel campione B il valore più basso degli 8 maggiori, cioè il valore critico inferiore, è 225.

Ne deriva che la distanza massima tra le due serie campionarie, per non rifiutare l’ipotesi nulla H₀, è la differenza tra questi due valori critici, cioè

303 – 225 = 78

Quindi si può rifiutare l’ipotesi nulla H₀ solo quando

q_B - q_A > -78

 

7 – Con ragionamento simile, ma simmetrico, in un test bilaterale si rifiuta l’ipotesi nulla anche quando la distribuzione è sbilanciata  con intensità uguale nell’altra direzione.

 

 

 

 

Nel gruppo A, dopo i due valori estremi, il primo dato è 226; nel gruppo B il primo dato dopo gli 8 valori più bassi (in quanto 2 + 8sono gli 11 dati minori della mediana generale) è 426.

Poiché

426 – 226 = 200

 si rifiuta l’ipotesi nulla H₀ solo quando

q_B - q_A > 200.

 

8 – Si deve quindi concludere che, alla probabilità nominale del 95%, l’intervallo di confidenza per la differenza mediana in questi due campioni è tra –78  e  +200.

 

Nel trarre le conclusioni  su questi risultati, è importante evidenziare due osservazioni:

-          la probabilità reale di questo intervallo di confidenza è del 97% (non del 95% come nominalmente richiesto), poiché è stato escluso un 1,5% in ogni coda della distribuzione, a causa dei valori discreti che il metodo esatto di Fisher determina quando i campioni sono piccoli;

-          con il test t (rivedi come si calcola l’intervallo di confidenza di una differenza tra le medie di due campioni indipendenti),

 

-          alla probabilità del 95% (quindi minore di quello reale prima utilizzato) l’intervallo di confidenza della differenza media risulta

–142,94  < d <  + 172,04

 

E’ più ampio di quello stimato con il test della mediana (-78  e  200) e il metodo delle probabilità esatte di Fisher. La causa è la forte asimmetria della distribuzione sperimentale, che inoltre solleva dubbi forti di validità quando si ricorre ad un test parametrico.

Sono più che evidenti i vantaggi di questo metodo, che inoltre è il meno potente tra quelli non parametrici, rispetto al metodo classico utilizzato nella statistica parametrica.