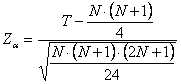METODI NON PARAMETRICI PER UN CAMPIONE

7.11. INTERVALLI DI CONFIDENZA DELLA LOCAZIONE (MEDIANA) CON IL T DI WILCOXON; MEDIE DI WALSH O QUASIMEDIANS, STIMATORE DI HODGES – LEHMANN O PSEUDOMEDIAN

Come già accennato in precedenza, è possibile ottenere l’intervallo di confidenza della tendenza centrale anche mediante alcuni metodi non parametrici. Tra i più diffusi e semplici, è da ricordare la stima di locazione (in questo caso la mediana) basata sui ranghi, proposta da J. L. Jr. Hodges e E. L. Lehmann nel 1963 (vedi l’articolo Estimation of location based on rank test, pubblicato su Annals of Mathematical Statistics vol. 34, pp. 598-611).

Tale valore, chiamato stimatore di Hodges – Lehmann (Hodges – Lehmann estimator), utilizza le medie di Walsh (Walsh averages) e il suo intervallo di confidenza, che permettono di individuare la tendenza centrale e la dispersione di una serie di misure, sono calcolati applicando in modo alternativo i valori critici del T di Wilcoxon.

Quando la distribuzione dei dati è fortemente asimmetrica, i testi consigliano l’uso della distribuzione binomiale. L’uso di questo metodo è consigliato quando

- i dati sono effettivamente dei ranghi oppure

- misure su una scala di intervalli o di rapporti, ma con una asimmetria media, che non permette di utilizzare la distribuzione t di Student.

Il metodo con la distribuzione T di Wilcoxon può essere compreso con facilità, sviluppando in tutti i passaggi logici un esempio preso dal testo di statistica non parametrica di P. Sprent pubblicato nel 1993 (Applied Nonparametric Statistical Methods, 2^nd ed., Chapman & Hall, London, 338 p.).

Si supponga, in un esperimento di tossicologia o di farmacologia, di avere misurato in 12 campioni, con dimensioni molto variabili e/o ignote, la percentuale di individui che reagiscono ad un principio attivo, ottenendo il seguente risultato

Campione	A	B	C	D	E	F	G	H	I	L	M	N
	15,7	4,9	6,0	7,7	17,6	4,5	5,7	5,3	12,3	9,6	13,5	12,3

Per convenienza didattica e semplificazione delle procedure, è stato scelto un esempio senza ties.

Quale è la mediana reale e quale il suo intervallo di confidenza?

Come già illustrato, nella pratica sperimentale il problema si pone quando sono note le percentuali di risposta, ma non le dimensioni di ogni campione, per cui non è possibile ricavare , cioè la media ponderata, e quindi nemmeno

- la sua varianza:

- e gli intervalli fiduciali mediante la distribuzione Z.

Oppure quando si vuole conoscere la risposta percentuale, ottenibile genericamente in esperimenti di questo tipo.

La metodologia prevede i seguenti passaggi logici.

1 - Si ordinano i valori sperimentali in modo crescente, come

Rango	1	2	3	4	5	6	7	8	9	10	11	12
	4,5	4,9	5,3	5,7	6,0	6,9	7,7	9,6	12,3	13,5	15,7	17,6

2 – Di essi si calcolano le cosiddette medie di Walsh (Walsh averages), introdotte da J. E. Walsh nel 1949 con un articolo sulla significatività dei test sulla mediana che possono essere ritenuti validi in condizioni molto generali (vedi Some significance tests for the median whish are valid under very general condition, pubblicato su Annals of Mathematical Statistics vol. 40, pp. 64-81). Per definizione le Walsh Averages, chiamate anche quasimedians,

sono date da

per i = 1 , 2, …, n e con tutte le j ³ i

Se i dati sono N, il loro numero è

3 - Come numero e rango, le Walsh Averages corrispondono ai valori di T nel test di Wilcoxon;

se è vera l’ipotesi nulla e le differenze sono sia positive che negative,

- il numero di medie di Walsh positive è uguale a T⁺,

- il numero di medie di Walsh negative è uguale a T^-

Nel caso dell’esempio, in cui le differenze sono tutte positive, esse sono distribuite come T e possono essere utilizzate come i valori T. (La dimostrazione di questa corrispondenza è lunga e ha un interesse pratico limitato; di conseguenza, sono qui riportate solamente le sue utilizzazioni.)

Con i dati dell’esempio (N = 12), esse sono 78

con la distribuzione riportata nella tabella seguente

	4,5	4,9	5,3	5,7	6,0	6,9	7,7	9,6	12,3	13,5	15,7	17,6
4,5	4,5	4,7	4,9	5,1	5,25	5,7*	6,1	7,05	8,04	9,0*	10,1	11,05
4,9		4,9	5,1	5,3**	5,45	5,9	6,3	7,25	8,6	9,2	10,3	11,25
5,3			5,3**	5,5	5,65	6,1	6,5	7,45	8,8	9,4	10,5	11,45
5,7				5,7*	5,85	6,3	6,7	7,65	9,0*	9,6	10,7	11,65
6,0					6,0	6,45	6,85	7,8	9,15	9,75	10,85	11,8
6,9						6,9	7,3	8,25	9,6	10,2	11,3	12,25*
7,7							7,7	8,65	10,0	10,6	11,7	12,65
9,6								9,6	10,95	11,55	12,65	13,6**
12,3									12,3	12,9	14,0	14,95
13,5										13,5	14,6	15,55
15,7											15,7	16,65
17,6												17,6

Walsh averages di 12 percentuali

4 – La mediana di questa distribuzione di medie è una stima della tendenza centrale. E’ chiamata Hodges – Lehmann estimator in alcuni testi, pseudo-median in altri.

Con 78 medie, questa mediana cade tra il 39° e il 40° valore. Poiché queste medie sono distribuite in modo crescente da sinistra a destra e dall’alto al basso, è semplice osservare che il 39° e il 40° valore sono entrambi 9,0 e quindi la mediana di queste medie o pseudomediana della distribuzione dei 12 valori originali dei è 9,0.

5 – Data la corrispondenza tra i ranghi di queste medie di Walsh e la distribuzione dei valori T di Wilcoxon, per calcolare l’intervallo si deve ricorre alla tabella dei valori critici di T.

Per le probabilità classiche in una distribuzione bilaterale per N = 12 nella tabella

- per a = 0.05 è riportato T = 13

- per a = 0.01 è riportato T = 7

6 – Il rango simmetrico dei limiti fiduciali è ottenuto sottraendo questo valore critico di T alla mediana di Walsh, cioè alla media che occupa il rango

In questo modo, si esclude il numero T di medie di Walsh da ogni estremità della serie dei ranghi.

Significa che, nella matrice triangolare delle Walsh averages, l’intervallo fiduciale della mediana (9,0)

- per a = 0.05 ha come estremi i valori compresi tra la 13^a media minore (5,7*) e la 13^a media maggiore (12,25*), cioè 5,7 < q < 12,25;

- per a = 0.01 ha come estremi i valori compresi tra la 7^a media minore (5,3**) e la 7^a media maggiore (13,6**), cioè 5,3 < q < 13,6.

E’ semplice osservare che questa distribuzione non simmetrica, come d’altronde quella dei dati. A differenza di altri metodi non parametrici, questa procedura riesce a fornire un intervallo non troppo grande. Con il test dei segni, alla probabilità a = 0.05 come già dimostrato l’intervallo di confidenza di questi dati campionari è compreso tra 5,3 e 13,5; cioè 5,3 < q < 13,5

Nello stesso modo di tutti gli intervalli fiduciali, anche questo può essere utilizzato per verificare la significatività della differenza tra la media di un campione e la media attesa, per un test bilaterale: se il valore di confronto è compreso nell’intervallo, non è possibile rifiutare l’ipotesi nulla alla probabilità a prefissata.

Nel caso di campioni grandi, con N > 20, le tabelle non riportano i valori critici di T. E’ possibile ricorrere a una sua stima approssimata.

Dalla formula generale, già riportata in forma più sintetica, del test T di Wilcoxon per grandi campioni