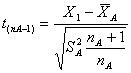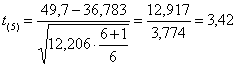INFERENZA SU UNA O DUE MEDIE CON IL TEST t DI STUDENT

 

 

6.3.   CONFRONTO TRA UNA OSSERVAZIONE E LA MEDIA DI UN CAMPIONE

Nelle rilevazioni in natura ed in laboratorio, sovente sorge il problema che una certa misura possa essere errata, rispetto alle altre del campione raccolto. Le cause possono essere le più diverse: l’imperizia del nuovo rilevatore rispetto all’esperto che ha raccolto gli altri dati, il funzionamento non corretto dello strumento, una condizione ambientale differente, il materiale o i reagenti di qualità diversa, una procedura nuova o applicata in modo non corretto. In altri casi, come in tassonomia, sorge il problema di verificare se l’individuo che si sta analizzando possa essere di un’altra popolazione rispetto alle unità già raccolte.

La verifica a questi sospetti, che può essere condotta con un test unilaterale o bilaterale secondo le ipotesi formulate,

è fatta mediante un test t:

 

dove

   X₁   = singola  rilevazione da verificare;       =  media del campione A;  

      =  varianza del campione A;     n_A   =   numero di osservazioni del campione A.

 

 

ESEMPIO.   Si vuole verificare se una misura (49,7) può essere ritenuta diversa dalle 6 del campione raccolto (40,3  -  38,8  -  33,5  -  38,6  -  31,9  -  37,6).

 

Risposta.  La media del campione (  ) è uguale a 36,873 e la varianza (  ) risulta uguale a 12,206. Da essi deriva

 il valore di t con 6-1 gdl

 che risulta uguale a 3,42.

I valori critici di t con 5 gdl, per un test a una coda, sono

-  2,015 alla probabilità a = 0.05;

-  3,365 alla probabilità a = 0.01

-  5,893 alla probabilità a = 0.001.

 

Per un test a due code, i valori critici riportati nella tabella sono

-  2,571 alla probabilità a = 0.05

-  4,032 alla probabilità a = 0.01.

 

Se è stato fatto un test bilaterale (il valore è diverso da quelli del campione?) si rifiuta l’ipotesi nulla con probabilità a compresa tra 0.05 e 0.01.

Se il test era unilaterale (il valore è maggiore di quelli del campione?), si respinge l’ipotesi nulla con probabilità a compresa tra 0.01 e 0.001.