|
INFERENZA SU UNA O DUE MEDIE CON IL TEST t DI STUDENT
6.10. POTENZA A PRIORI E A POSTERIORI DEL TEST t, CON UN CAMPIONE E CON DUE CAMPIONI DIPENDENTI O INDIPENDENTI
Quando si programma un esperimento, la prima domanda è quasi sempre: “Quanti dati devo raccogliere?” Effettuato un test, se il risultato non è significativo è importante rispondere al quesito: “Con il campione raccolto, che probabilità avevo che il test risultasse significativo?” La prima domanda, chiamata anche potenza a priori, e la seconda, potenza a posteriori, hanno già avuto una prima risposta nel capitolo IV, con l’uso della distribuzione Z.
Ricordando i concetti principali, - il numero (n) di dati necessari a rendere significativo un test e - la misura della sua potenza (1-b) possono essere stimate sulla base delle relazioni che esistono tra 5 quantità: 1 - la probabilità a alla quale il test t di Student dovrebbe risultare significativo, dopo aver raccolto i dati; per essa deve essere specificata pure la direzione dell’ipotesi H1, se unilaterale oppure bilaterale;
2 - la probabilità b (sempre unilaterale), cioè il rischio che si intende correre che il test non risulti significativo; questo concetto risulta più chiaro utilizzando quello, ad esso alternativo, di potenza (1-b), cioè della probabilità di rifiutare (correttamente) l’ipotesi nulla, quando essa è falsa;
3 - la differenza
d che a priori si intende dimostrare
significativa (con d uguale alla differenza tra m e m0 quando si applica
il test ad un campione oppure alla differenza tra m1 e m2 nel caso di due
campioni indipendenti); la differenza campionaria d per un test a
posteriori (con d uguale a
4 - la varianza s2 del fenomeno, misurata su uno studio pilota o un campione preliminare quando la varianza reale s2 è ignota;
5 - la dimensione n del campione.
L’uso di s2 al posto di s2 impone il ricorso alla distribuzione t in sostituzione della distribuzione z. Quando n è sufficientemente grande, - la distribuzione normale Z e la distribuzione t praticamente coincidono, fornendo risposte molto simili; - le differenze sono ritenute importanti, quando il campione ha meno di 30 osservazioni e quindi i gdl del t sono una quantità limitata.
A differenza della distribuzione normale Z, che è unica, la distribuzione t di Student è formata da una intera famiglia di distribuzioni, una per ogni grado di libertà. Per stimare le dimensioni (n) del campione, occorre quindi - iniziare da un valore di t che dipende da n, non ancora calcolato; - di conseguenza, per ottenere n si deve utilizzare un metodo iterativo, che stima n con approssimazioni successive, sempre più vicine al valore reale (in pratica, sono sufficienti due o al massimo tre calcoli).
Una impostazione didattica chiara e semplice dei concetti e dei metodi relativi alla potenza di un test richiede solo tre formule, una per ognuna delle tre quantità fondamentali che servono al ricercatore per verificare l’ipotesi nulla sulle medie attraverso il test t di Student.
Esse forniscono un aiuto importante - sia nella programmazione di un esperimento, cioè nella fase iniziale di ogni ricerca empirica chiamata disegno sperimentale, - sia nella discussione del risultato, che dovrebbe avvenire sempre, dopo la raccolta dei dati e l’applicazione del test.
Queste tre quantità, delle cinque elencate in precedenza, sono: - n, le dimensioni richieste (o minime) del campione, necessarie per rifiutare l’ipotesi nulla, - d, la differenza utile (o minima) che si vuole dimostrare significativa con i dati raccolti, - 1-b, la potenza del test.
Le altre due quantità fondamentali sono meno condizionate dal ricercatore: - s2, la varianza campionaria, poiché dipende dalla natura dei dati ed è tipica di ogni fenomeno biologico e naturale, - a, prefissata dal ricercatore ma in modo standard, quale la convenzione sui valore soglia (0.05 – 0.01 – 0.001) dei limiti di significatività, oppure sulla base di fattori esterni all’esperimento, quale il rischio che egli corre se la conclusione si rivelasse errata (vedi capitolo IV, sui criteri per scelta del valore di a).
Il calcolo delle tre quantità fondamentali (n, d, 1-b) utilizza gli stessi concetti, ma ricorre a formule leggermente differenti, se sono riferite al caso di: - un campione oppure due campioni dipendenti, in quanto utilizza solo la colonna delle differenze, - due campioni indipendenti, in cui si utilizzano entrambe le serie di rilevazioni. Affinché, con un campione o con due campioni dipendenti, la differenza tra la media campionaria e la media attesa oppure la media delle differenze e quella attesa risultino significative, cioè per rifiutare l’ipotesi nulla H0: m = m0 nel caso di un campione, H0: d = 0 nel caso di due campioni dipendenti
- il numero minimo di osservazioni n (numero di dati in un campione e numero di coppie in due campioni dipendenti) deve essere n ³ ( ta,n + tb,n )2 ×
- la differenza minima che può risultare significativa d è
- la potenza 1-b del test, stimata conoscendo b, è
ESEMPIO 1. Ad un tecnico di laboratorio è stato chiesto di valutare se la concentrazione di una sostanza utilizzata per conservare un alimento (in grammi di sostanza secca per Kg di alimento) differisce di oltre 1 gr. dalla quantità stabilita, ritenuta ottimale: può avere conseguenze negative sia se in difetto sia se in eccesso. Dopo alcune misure campionarie (12,5; 13,1; 14,7; 12,8;…) per avere una misura della variabilità, egli ha stimato la varianza dei suoi campioni ottenendo s2 = 3,24. Quanti misure deve effettuare per dimostrare che - la quantità media di conservante si discosta di almeno un 1 gr. dalla quantità ritenuta ottimale - alla probabilità del 95% - e abbia una probabilità del 90% di ottenere il risultato richiesto?
Risposta. Dalla presentazione del problema, si ricava:
- a = 0.05 in un test bilaterale; di esso occorre conoscere il valore di t; ma poiché nella tabella dei valori critici sono richiesti anche i gdl, in prima approssimazione si può assumere che servano circa 30 dati (n = 29); quindi t(0.025; 29) = 2,045
- b = 0.10 in un test unilaterale; il valore di t, sempre per il numero di dati preventivato in prima approssimazione (n = 29), è t(0.10; 29) = 1,3114 - s2 = 3,24 - d = 1,0 Da essi con n ³ ( ta,n + tb,n )2 × si calcola un primo valore n ³ (2,045 + 1,3114
)2 × che risulta n = 36,5. Poiché il valore calcolato (36,5) si discosta da quello iniziale (30), - si devono individuare i valori di t corrispondenti alla nuova stima. Tuttavia, spesso la tabella non riporta i valori espressa richiesti, come quello di t per 36 gdl. Essa riporta solamente i valori critici per 35 o 40 gdl, si può utilizzare quello di n = 35: - per a = 0.05 esso risulta t(0.025; 35) = 2,030 - per b = 0.010 esso risulta t(0.10; 35) = 1,3062
Con essi si ottiene n ³ (2,030 +
1,3062)2 × una seconda stima: n = 36,06. Praticamente è identica alla stima precedente, poiché il risultato può essere solo un intero. Arrotondando in eccesso, servono almeno 37 dati.
ESEMPIO 2. Se il tecnico, a causa del tempo richiesto e dei fondi a disposizione, valutasse che può effettuare solo 20 misure, quale differenza minima potrà dimostrare significativa, ovviamente a parità degli altri 3 parametri? (a, direzione dell’ipotesi H1, b)
Risposta. Poiché - n = 19 - per a = 0.05 bilaterale il valore di t(0.025; 19) è 2,093 - per b = 0.10 unilaterale il valore di t(0.10; 19) è 1,3277 con
si calcola una differenza minima
che risulta d = 1,38. Non potrà verificare, cioè non potrà dimostrare significativa, una differenza d inferiore a 1,38.
ESEMPIO 3. Raccolti i 20 dati, che probabilità avrebbe avuto il tecnico di evidenziare una differenza pari a 1 gr. rispetto al valore atteso?
Risposta. Per stimare la potenza (1-b) del test, si deve calcolare il valore tb e poi da esso la probabilità b. Con - d = 1 - e gli altri parametri uguali all’esempio 2 mediante
si calcola
un valore del t uguale a 0,385 con 19 gdl. Purtroppo le tabelle sinottiche riportano solamente alcuni valori per le probabilità fondamentali. Da quella unilaterale, per n = 19, il valore critico per b = 0.25 (anche per b si utilizza la tabella a) è 0,6876. Di conseguenza, la probabilità b è nettamente maggiore di 0.25. Poiché la potenza del test è 1-b, la probabilità di rifiutare una differenza d pari a 1 gr. è ampiamente inferiore a 0.75. Nel caso di due campioni indipendenti, affinché la differenza d tra le due medie m1 e m2 risulti significativa, 1 - per ognuno dei due gruppi, il campione deve avere dimensioni minime n n ³ ( ta,n + tb,n )2 ×
2 - la differenza minima d che può risultare significativa è
3 - la potenza 1-b del test, stimata conoscendo b, è
Rispetto al caso precedente, riguardante un campione o due campioni dipendenti, con due campioni indipendenti nella scelta dei valori ta e tb i gradi di libertà(n) non sono n-1, ma 2n-2, poiché il numero di dati complessivo utilizzato nei due gruppi a confronto è uguale a 2n.
ESEMPIO 4. Si
vuole verificare se una sostanza tossica, somministrata con il cibo a cavie,
determina un accrescimento più limitato, rispetto alla situazione normale. Da
un esperimento pilota su due gruppi di animali (sperimentale e controllo) è
stata stimata la crescita (in millimetri) dopo 20 giorni e la varianza comune Per programmare un test in cui una differenza di 0,4 millimetri tra le dimensioni medie dei due gruppi risulti significativa alla probabilità 0.05 e la probabilità di scoprire tale differenza sia pari a 0.9, quanti individui servono?
Risposta. Dalla presentazione del problema, si ricava: - a = 0.05 in un test unilaterale; di esso occorre conoscere il valore di t; ma poiché nella tabella dei valori critici sono richiesti anche i gdl, in prima approssimazione si può assumere che servano circa 30 dati per gruppo (n = 58); quindi t(0.05; 58) = 1,6716
- b = 0.10 in un test unilaterale; il valore di t, sempre per il numero di dati preventivato in prima approssimazione (n = 58), è t(0.10; 58) = 1,2963 - - d = 0,4. Da essi con n ³ ( ta,n + tb,n )2 × si ottiene una dimensione minima di ognuno dei due gruppi
pari a 60 individui. La differenza tra i 30 preventivati e i 60 stimati è grande; di conseguenza, si deve procedere ad una seconda stima, usando i valori di t corrispondenti a n = 118. Poiché nella tabella il valore più vicino è quello per n = 120, è possibile servirsi di questo valore (quando i gdl sono così alti, la differenza tra i valore di t è minima). In una distribuzione ad una coda, - per a t(0.05; 120) = 1,6577 - per b t(0.10; 120) = 1,2886 la seconda stima
calcola n = 58,60. Poiché il risultato differisce poco dal precedente (calcola 59 rispetto ai 60 della prima stima), anche senza passare al terzo tentativo si può concludere che - ognuno dei due gruppi debba essere formato da almeno n = 60 individui, per un totale n = 120.
ESEMPIO 5. Se il ricercatore dispone solo di 80 cavie, formando due gruppi di 40 individui quale è la differenza minima d che potrà dimostrare significativa, alle stesse condizioni del test precedente?
Risposta. Poiché - n = 78 - per a = 0.05 unilaterale il valore di t(0.025; 78) è 1,6646 - per b = 0.10 unilaterale il valore di t(0.10; 78) è 1,2925 con
si calcola una differenza minima
d uguale a 0,486. Non potrà verificare, cioè non potrà risultare significativa, una differenza d inferiore a 0,486.
ESEMPIO 6. Effettuando un esperimento con 40 dati per gruppo, che probabilità avrebbe avuto di evidenziare una differenza pari a 0,4 tra le due medie?
Risposta. Per stimare la potenza (1-b) del test, si deve calcolare il valore tb e poi da esso la probabilità b. Con - d = 0,4 - e gli altri parametri uguali all’esempio 5 mediante
stima
un valore del t uguale a 0,77 con 78 gdl. Purtroppo le tabelle sinottiche spesse riportano solamente alcuni valori.
Da quella unilaterale, per n = 78, - il valore critico per b = 0.25 (nella tabella è indicato a, ma le due distribuzioni sono identiche) è 0,6776 - il valore critico per b = 0.10 è 1,2925.
Di conseguenza, la probabilità b è leggermente minore di 0.25. Poiché la potenza del test è 1-b, la probabilità di rifiutare una differenza d pari a 0,4 è di poco superiore a 0.75.
L’uso della distribuzione t di Student per calcolare la probabilità di b (o la potenza 1-b) fornisce una risposta approssimata, poiché vincolata alla probabilità riportate nelle tabelle sinottiche: se il valore calcolato non coincide esattamente con uno dei valori riportati, ci si deve limitare ad indicare un intervallo entro il quale la probabilità è compresa, ad esempio, tra 0,2 e 0,1 oppure tra 0,025 e 0,05 come evidenzia l’intestazione della tabella sottostante, che riporta le probabilità di norma utilizzate nelle tavole sinottiche dei testi di statistica.
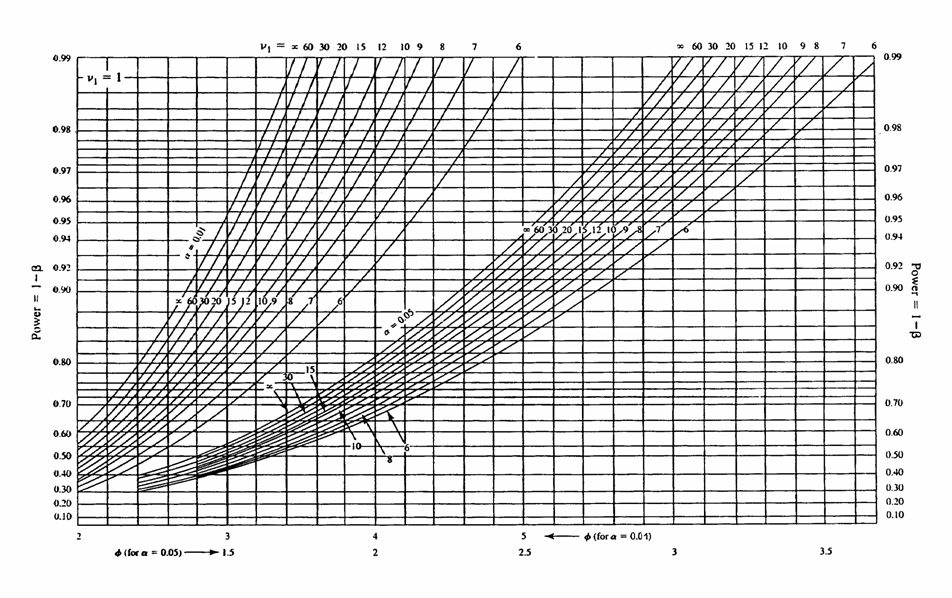
Per una risposta più precisa, nel caso di due o più campioni è possibile ricorre ai metodi grafici. Diffusi da tempo, ora queste tecniche appaiono superate dai programmi informatici, con i quali la stima della probabilità (a e b) è fornita alla seconda cifra decimale, a causa dell’ampia memoria dei computer.
Per entrare in un grafico di curve di probabilità 1-b, come riportato nella pagina successiva, servono 4 informazioni: 1 - il numero di gruppi a confronto, in questo caso sono 2: in una ANOVA corrispondono n = 1, i gdl della varianza tra trattamenti; 2 - la probabilità a per la quale si programma la significatività del test; questi grafici riportano solo le curve per a = 0.01 e a = 0.05; 3 - il valore di f (phi) ottenuto con la formula seguente, in accordo con la simbologia consueta
4 - il numero n di dati in ogni gruppo, che devono essere distribuiti in modo bilanciato (n1 = n2).
(Maggiori informazioni sulla costruzione di questo grafico sono riportate nel paragrafo sulla potenza in un test ANOVA)
Complessa nella costruzione, questa procedura è semplice nella sua utilizzazione: 1) Il grafico riportato può essere utilizzato solo - in un test bilaterale - per la probabilità a = 0.01 (ultima riga inferiore) e per la probabilità a =0.05 (prima riga sotto la figura, appena sopra la precedente).
2) Una volta scelta la probabilità a e stimato il valore di f (phi) che - per la probabilità a = 0.01 varia approssimativamente da 1,5 a 3,5 per una potenza che varia da 0.30 a 0.99 in rapporto a n, - per la probabilità a = 0.05 varia da 2 a 5 sempre per una potenza 1-b che varia da 0.30 a 0.99 in rapporto a n,
3) dall’asse dell’ascissa si sale perpendicolarmente dal valore di f lungo le rette tracciate (parallele all’ordinata) fino ad incontrare la curva dei gdl n, dove n = 2(n-1);
4) da quel punto, spostandosi lateralmente lungo le rette parallele all’ascissa si giunge all’ordinata, dove (riportato sia a destra sia a sinistra) si legge il valore della potenza, la probabilità 1- b.
In conclusione, per risalire da f alla potenza 1-b servono altri due valori: a, n2; - il primo solo per le due probabilità ricordate, - il secondo per gli 11 gdl riportati (6, 7, 8, 9, 10, 12, 15, 20, 30, 60, ¥ ); per altri gdl, si deve interpolare tra le due curve che li comprendono.
ESEMPIO 7. Stimare il valore di b sia a) con il test t (bilaterale) che b) con l’uso del grafico, in un esperimento programmato per valutare, - alla probabilità a = 0.05, - se due sostanze tossiche hanno effetti che differiscono di una quantità d = 1 - utilizzando 15 osservazioni per gruppo: n1 = n2 = 15. Un esperimento pilota ha fornito una - stima della
varianza associata
Risposta A) Con - gdl n = 2(n-1) = 28 - un valore di t alla probabilità a = 0.05, per un test bilaterale uguale a 2,048 t0.025,28 = 2,048 si stima un valore di t per la probabilità b (sempre unilaterale)
uguale a 1,75 Poiché il valore critico di t unilaterale con 28 gdl - alla probabilità 0.05 è uguale a 1,7011 - alla probabilità 0.025 è uguale a 2,0484 la probabilità b stimata è compresa tra 0.05 e 0.025; di conseguenza la potenza 1-b è compresa tra 0,95 e 0,975.
B) Utilizzando il grafico, si ottiene un valore di f (phi)
uguale a 2,685
Nel grafico delle curve di potenza, - nella riga a = 0.05 (ultima riga), il valore di 2,685 può essere collocato approssimativamente vicino alla seconda riga verticale dopo 2.5; - salendo perpendicolarmente, si incontra la curva per n = 30 in un punto che, proiettato sull’asse delle ordinate, cade tra 0.95 e 0.96. La potenza di questo test è appunto compresa tra 0.95 e 0.96. La precisione della potenza stimata dipende dalle caratteristiche del grafico. Spesso è più dettagliato di quello che è stato qui utilizzato ai soli fini di illustrare i concetti e le procedure.
I metodi descritti per 2 campioni sono utili a priori, nella fase di programmazione dell’esperimento, per avere un’idea di - quanti dati n raccogliere, - quale sia la differenza d che è possibile evidenziare come significativa, - la potenza 1-b del test, se esso verrà
effettuato seguendo le idee espresse nella programmazione, dopo aver misurato
la varianza associata
A posteriori, dopo la raccolta dei dati spesso attuata senza la programmazione appena indicata, può avvenire che il test non risulti significativo. Per comprenderne le cause, per valutare se la significatività non dimostrata molto probabilmente nella realtà non esiste oppure è dovuta ad un errore nella realizzazione dell’esperimento, diventa importante il calcolo della potenza, poiché b fornisce la probabilità di commettere l’errore di II Tipo.
Nel caso di 2 campioni indipendenti, avviene spesso che essi siano formati da un numero differente di osservazioni (n1 ¹ n2); per utilizzare le formule precedenti, n è calcolato attraverso la media armonica. Dalla formula generale per k gruppi
n = nel caso di 2 soli campioni si ricava - la formula abbreviata n = Il valore del f è ottenuto da
f = dove - n, il numero di dati in ognuno dei 2 gruppi, è stimato con la formula precedente quando n1 ¹ n2 - d è la differenza campionaria tra le
due medie: d = - - la potenza 1- b è stimata dal valore f con n = n1 + n2 - 2
ESEMPIO 8. Per verificare la differenza tra il livello medio d’inquinamento di due corpi idrici, sono state effettuate 8 prelievi (n1 = 8) nel primo e 6 (n2 = 6) nel secondo, ottenendo - - Stimare A) la significatività della differenza tra le due medie B) la potenza del test effettuato.
Risposta A) E’ un test bilaterale, con H0: m1 = m2 H1: m1 ¹ m2 nel quale
il t con 12 gdl risulta uguale a 1,863. Poiché, come riportato nella tavola sinottica, il valore di t bilaterale con n = 12 - alla probabilità a = 0.20 è uguale a 1,356 - alla probabilità a = 0.10 è uguale a 1,782 - alla probabilità a = 0.05 è uguale a 2,8179 si deve concludere che non è possibile rifiutare l’ipotesi nulla, per il livello di significatività del 5%: la probabilità di trovare una differenza uguale o superiore a quella misurata si trova tra il 10 e il 5 per cento (più vicina al 10%).
B) La potenza del test, vale a dire la probabilità di rifiutare (correttamente) l’ipotesi nulla quando è falsa, trattandosi di - un test bilaterale - per un valore critico di a = 0.05 - oppure a = 0.01 può essere stimata mediante il valore di - f con n = n1 + n2 – 2 e l’uso del grafico presentato. Con due campioni non bilanciati, - dapprima si stima n
che risulta uguale a 6,86 (osservare ancora una volta come campioni non bilanciati facciano perdere informazione, essendo n minore della media aritmetica, che si otterrebbe con due gruppi formati da 7 repliche) - successivamente la differenza
campionaria tra le due medie: d = si stima f f =
che risulta uguale a 1,11. Nel grafico, alla probabilità a = 0.05 il valore di f =1,11 si trova a sinistra del valore minimo 1,5 riportato. Presumibilmente incontra la curva con 12 gdl con un valore di potenza intorno a 0.40. Per a = 0.01 è nettamente inferiore al valore 2 riportato come minimo e quindi la potenza ha un valore intorno a 0.30 o minore.
In conclusione, anche se a è risultata minore del 10%, vi era - una probabilità b intorno al 60% che il test non risultasse significativo per a = 0.05 - una probabilità b intorno al 70% che il test non risultasse significativo per a = 0.01
ESEMPIO 9. L’aumento del numero di dati, a parità degli altri parametri, accresce notevolmente la potenza del test. Rifare i calcoli dell’esempio 8, con 15 dati per gruppo (n = n1 = n2 = 15).
Risposte. A) Il test t
sarebbe risultato uguale a 1,863 con 28 gdl. Poiché, nella tavola sinottica, il valore di t bilaterale con n = 28 - alla probabilità a = 0.05 è uguale a 2,368 - alla probabilità a = 0.025 è uguale a 2,763 - alla probabilità a = 0.01 è uguale a 3,047 si sarebbe rifiutata l’ipotesi nulla alla probabilità del 5 per cento: la probabilità di trovare una differenza uguale o superiore a quella misurata si sarebbe trovata tra il 2,5 e l’1 per cento (appena inferiore al 2,5%).
B) Per stimare la potenza del test, si calcola f f = che risulta uguale a 1,82. Nel grafico, alla probabilità a = 0.05 il valore di f = 1,82 si trova a destra del valore minimo 1,5 riportato. Approssimativamente, incontra la curva con n = 28 (nel grafico n = 30) per un valore di potenza (1-b) intorno a 0.70. Vi era una probabilità del 30% di commettere l’errore b, cioè di non rifiutare l’ipotesi nulla alla probabilità a = 0.05.
| |||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||
nel caso di due campioni indipendenti);
11,27 
è risultata uguale
0,54.
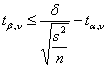
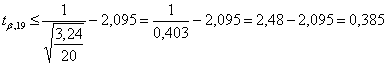
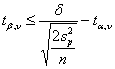
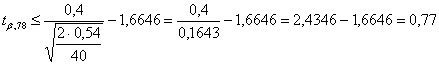
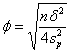
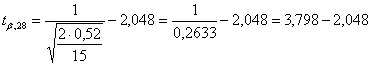= 1,75
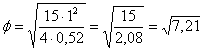= 2,685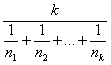
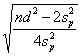
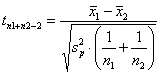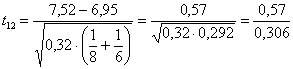= 7,52 e 
= 6,95
= 
= 1,863
= 
= 6,86
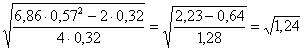= 1,11
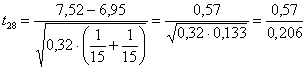= 2,767
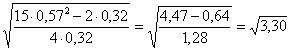= 1,82