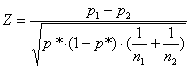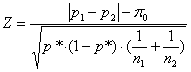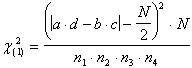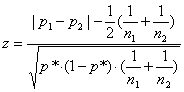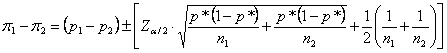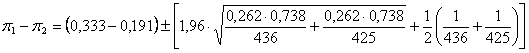PROPORZIONI  E  PERCENTUALI,  RISCHI,  ODDS  E  TASSI

 

 

5.13.  SIGNIFICATIVITA’ E INTERVALLO DI CONFIDENZA DELLA DIFFERENZA TRA DUE PROPORZIONI, CON LA DISTRIBUZIONE NORMALE.

 

 

Quando i campioni sono grandi, oltre le 200 unità secondo le indicazioni di vari autori recenti, la significatività della differenza tra due proporzioni campionarie   può essere verificata

-  sia con il test c² e il test G,

-  sia con la distribuzione  normale ridotta Z, a motivo dell’approssimazione alla normale.

Anche in questo caso, viene riassunto quanto esposto già in modo dettagliato nel capitolo III.

 

Per verificare l’ipotesi di una diversa incidenza delle malattie polmonari in aree ad alto e a basso inquinamento, ai fini dell’inferenza sulla differenza tra le due proporzioni, quindi per la verifica di

H₀:       oppure      H₀:

 è possibile presentare gli stessi dati

-  sia in tabelle di contingenza 2 x 2 come la seguente

 

 

-  sia con le proporzioni, come nella tabella seguente

 

La prima è l’impostazione dei dati per la formula classica del c²;

 la seconda, per applicare la formula che utilizza

 la distribuzione normale,

 dove

-  è la proporzione media ponderata dei 2 gruppi a confronto.

 e il risultato è uguale, poiché

 oppure

 

A differenza dei metodi classici del  e del metodo delle probabilità esatte di Fisher, con la distribuzione Z è possibile

-  valutare se la differenza tra le due proporzioni campionarie () è significativamente diversa da una proporzione attesa p₀; è la formula generale per la verifica di una differenza

 con

 

Con la correzione per la continuità di Yates, la formula del c²

-  per la significatività della differenza  rispetto a una differenza nulla

H₀:       equivalente a       H₀:  

 è

Nel test Z essa diviene

 

Per il semplice confronto tra due proporzioni con un test bilaterale, i metodi tradizionali sono il test esatto di Fisher (the Fisher’s exact test) e il test chi-quadrato con la correzione per la continuità di Yates (the chi-square test with Yate’s continuity correction).

Tuttavia, il ricorso alla distribuzione normale è frequente, poiché presenta 5 vantaggi rispetto al c². Infatti essa permette

1 –  la verifica di ipotesi unilaterali oltre a quelle bilaterali,

2 –  il confronto della differenza osservata tra due proporzioni (p₁ – p₂) con una differenza attesa (p),

3 –  la stima dell’intervallo fiduciale della differenza tra le due proporzioni,

4 –  di comprendere i parametri per il calcolo della potenza (1-b) del test, detta potenza a posteriori,

5 -  di comprendere i parametri per il calcolo del numero minimo () di dati necessario affinché il test risulti significativo, detto potenza a priori.

 

I primi due punti sono già stati illustrati nel capitolo III e rapidamente richiamati in questo paragrafo. Il punto 3 è presentato in questo paragrafo; i punti 4 e 5 saranno illustrati nel paragrafo successivo.

 

L’intervallo di confidenza della differenza reale tra due proporzioni a partire da quelle campionarie (p₁ – p₂)

 è dato da

 dove

-   p* è la frequenza media ponderata

-  a/2 è la probabilità prescelta in una distribuzione a due code

 

Questa procedura può essere utilizzata anche per verificare la significatività della differenza in un test bilaterale, poiché

-  se una differenza tra due proporzioni è esclusa da questo intervallo, essa è significativamente diversa dalla differenza (p₁-p₂) intorno al quale è stata costruito l’intervallo fiduciale, alla probabilità a prescelta.

 

ESEMPIO 1. Con un sondaggio presso medici di famiglia, è stata rilevata la proporzione di persone affette da malattie polmonari, tra coloro che vivono da almeno 10 anni in zone ad inquinamento atmosferico alto o basso della stessa città. La rilevazione ha fornito i seguenti risultati

 

 

 

 

Calcolare l’intervallo di confidenza della differenza vera tra le due proporzioni, con probabilità del 95% di affermare il vero.

 

Risposta.   Con 

-  p₁ = 0,333   e   n₁ = 436

-  p₂ = 0,191   e   n₂ = 425

-  p* = 0,262   e   Z = 1,96  (per a = 0.05 considerando ambedue le code della distribuzione)

 l’intervallo fiduciale della differenza

 è

 

 

uguale a 0,141 ± 0,061.

Quindi, con probabilità del 95% di affermare il vero, la differenza vera p₁ - p₂ è compresa tra

-   il limite inferiore L₁ = 0,080 (0,141 – 0,061),

-   il limite superiore L₂ = 0,202 (0141 + 0,061).

 

Ai fini dell’inferenza con un test bilaterale, si afferma che

 -  qualunque differenza risulti esclusa da questo intervallo, è significativamente differente da questa, in un test bilaterale alla stessa probabilità a = 0.05.