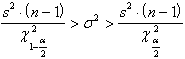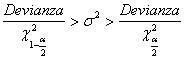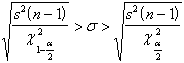VERIFICA DELLE IPOTESI

TEST PER UN CAMPIONE SULLA TENDENZA CENTRALE CON VARIANZA NOTA

E TEST SULLA VARIANZA

CON INTERVALLI DI CONFIDENZA

 

 

4.15.  intervallo di confidenza o di fiducia di una varianza, con equal tail method  E  shortest unbiased confidence intervals

 

 

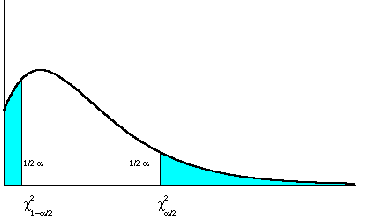
Il calcolo dell’intervallo di confidenza di una varianza richiede una procedura più complessa di quella illustrata per l’intervallo di confidenza della media. A differenza della distribuzione Z (utilizzata nei paragrafi precedenti) e della distribuzione t di Student (il cui impiego sarà illustrato nel capitolo relativo) che servono per test sulla media e hanno forma simmetrica, la distribuzione c², alla quale si ricorre per test sulla varianza, non è simmetrica, quando i campioni non sono grandi.

Approssimativamente, poiché varia in funzione dei gradi di libertà e quindi delle dimensioni del campione, ha la forma illustrata nella figura successiva.

E’ ovvio che le probabilità collocate ai due estremi dovranno essere stimate separatamente.

 

DISTRIBUZIONE  DEI  VALORI  DEL

CON UN NUMERO MEDIO DI GRADI DI LIBERTA’

 

I concetti illustrati nel paragrafo sul confronto tra una varianza campionaria e una attesa hanno dimostrato che

- il rapporto tra le devianza del campione  e la varianza della popolazione  da cui il campione è estratto

- segue la distribuzione  con gdl

 

Da questa legge di distribuzione, si può dedurre che

 con probabilità  il rapporto  sarà compreso

  tra i due valori estremi

       e       

 che rappresentano rispettivamente quello inferiore (a sinistra) e quello superiore (a destra).

Tale equazione può essere scritta come

 da cui si ricava che

l'intervallo di confidenza della varianza (s²) della popolazione, stimata a partire da una varianza campionaria ()

 è compreso entro i valori

 oppure, ancor meglio per i calcoli,

 

Di conseguenza, per la relazione esistente tra devianza e deviazione standard, è possibile anche scrivere che l'intervallo di confidenza della deviazione standard () della popolazione

 è delimitato dai valori estremi

 

Questo metodo, sia per la varianza  che per la deviazione standard  è chiamato equal tails method, poiché ai due estremi è collocata una quantità uguale di probabilità , come nella figura precedente.

 

ESEMPIO 1.   Si vuole conoscere l'intervallo di confidenza al 99% della varianza relativa alla presenza di solventi clorurati totali nell'atmosfera di una città.

Da un campione di 16 osservazioni, è stata misurata la quantità media d’inquinamento (in mg/m³ a 0° C e a 1013 mbar) e si è calcolata la varianza campionaria  = 82

Entro quali valori può trovarsi la varianza reale s² con probabilità del 99% di affermare il vero?

 

Risposta.   Dalla tabella del c², si devono rilevare i valori critici con gradi di libertà  = 15:

-  per  a = 0.995 (1 - 0.005) il valore è  = 4,605

-  per  a = 0.005. il valore è   = 32,85

L’intervallo di confidenza della varianza reale s²

 stimato con

 < s² <

 risulta

37,44 < s² < 267,10

In altri termini, con probabilità P = 0,99 è compreso tra

-  il limite inferiore L₁ = 37,44

-  il limite superiore L₂ = 267,10.

E' da mettere in evidenza come, rispetto al valore centrale ( = 82), i due estremi non siano simmetrici.

 

ESEMPIO 2.   Calcolare l'intervallo di confidenza al 95% della varianza reale s² del  carapace della specie Heterocypris incongruens. La varianza di un campione di 41 individui, (misurati in mm), è risultata uguale a 0,0412.

 

Risposta.   Dapprima si devono individuare i valori critici del c² con gradi di libertà   = 40:

-  per  a = 0.975 il valore è  = 24,44

-  per  a = 0.025. il valore è   = 59,20.

 

Successivamente si calcola l’intervallo

 

 e

0,0278 < s² < 0,0674

ricavando che come valori estremi esso ha 

-  L₁ = 0,0278

-  L₂ = 0,0674.

 

Per ottenere una stima corretta della varianza e del suo intervallo di confidenza, è sempre importante ricordare che

-  è condizione essenziale di validità che i dati siano distribuiti in modo normale.

La presenza di un solo valore anomalo è sufficiente per determinare una varianza campionaria molto maggiore di quella reale. Ma la normalità di una distribuzione campionaria è difficile da dimostrare, in particolare quando  è piccolo. Di conseguenza, quando la normalità della distribuzione campionaria non è certa, l'intervallo fiduciale di una varianza (quindi anche della deviazione standard) deve essere considerato con molta cautela.

Come già per la media, anche nel caso della varianza l’intervallo fiduciale può essere utilizzato per

-  valutare se un’altra stima campionaria s² si differenzia in modo significativo dal valore utilizzato per costruire l’intervallo di confidenza.

 

Il test con ipotesi nulla H₀:  e ipotesi alternativa H₁:

 alla  probabilità a

-  risulterà non significativo quando la varianza del secondo campione è compresa

-  mentre risulterà non  significativo quando  la varianza del secondo campione  non è compresa,

 nell’intervallo costruito intorno alla prima .

La proprietà è simmetrica e le due varianze possono esser scambiate: è possibile fondare l'analisi calcolando l’intervallo di confidenza dell’una oppure dell’altra (non di entrambe e vedere se hanno una zona di sovrapposizione).

 

Oltre

-  all’equal tails method qui illustrato, che rappresenta la procedura classica per calcolare l’intervallo di confidenza della varianza vera , è utilizzato anche un altro metodo seppure con una diffusione molto minore. E’ chiamato

-  shortest unbiased confidence intervals e è stato proposto da R. F. Tate e G. W. Klett nel 1959 con l’articolo Optimal confidence intervals for the variance of a normal distribution (pubblicato su Journal of the American Statistical Association Vol. 54, pp. 674 - 682).

Con questo metodo, si ottiene

-  l’intervallo di confidenza più breve (shortest), nel senso che il rapporto tra i due valori estremi

 è il minore possibile.

Per questo calcolo, si utilizzano i valori riportati nella tabella successiva. 

Essi sono costruiti in modo tale che

-  nel rapporto

- la quantità è un valore aggiustato di  oppure di

- che permette di ricavare l’intervallo di confidenza di  più breve possibile.

 

I valori della tabella sono stati pubblicati da D. V. Lindley, D. A. East e P. A. Hamilton nel 1960 sulla rivista Biometrika (Vol. 47 pp. 433-437). Per un uso ancora più semplice e immediato, sono stati rielaborati (divisi per i gradi di libertà )  da F. James Rohlf e Robert R. Sokal per le loro Statistical Tables (3^rd ed. W. H. Freeman and Company, New York, 1995, XIV + 199 p.).

Nella tabella successiva, dopo aver scelto

-  la riga , corrispondente ai gradi di libertà  della varianza campionaria ,

-  e la colonna corrispondente alla probabilità P (nella tabella sono riportate solo 95% e 99%)

 si identificano i due valori   e  .

I limiti dell’intervallo di confidenza sono:

-  il limite inferiore (lower limit)

-  il limite superiore (upper limit)

 

COEFFICIENTI PER DETERMINARE

I  SHORTEST UNBIASED CONFIDENCE LIMITS FOR THE VARIANCE

 

 

ESEMPIO 3. (STESSI DATI DELL’ESEMPIO 1, PER UN CONFRONTO DEI RISULTATI).  Si vuole conoscere l'intervallo di confidenza al 99% della varianza relativa alla presenza di solventi clorurati totali nell'atmosfera di una città.

Da un campione di 16 osservazioni, è stata misurata la quantità media d’inquinamento (in mg/m³ a 0° C e a 1013 mbar) e si è calcolata la varianza campionaria  = 82

Entro quali valori può trovarsi la varianza reale s² con probabilità del 99% di affermare il vero?

 

Risposta.   Dalla tabella, per  con gradi di libertà  = 15 si rilevano i coefficienti

    e   

L’intervallo di confidenza della varianza reale s² come limiti ha

-  il limite inferiore (lower limit)

- il limite superiore (upper limit)

 

Il rapporto  di questo intervallo

 risulta  uguale a 7,03

 mentre con il metodo classico o equal tails method si erano ottenuti

-  il limite inferiore L₁ = 37,44

-  il limite superiore L₂ = 267,10.

 e quindi

 un rapporto   = 7,13.