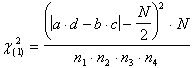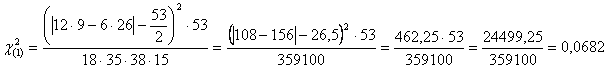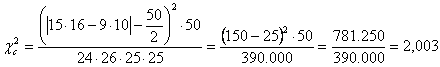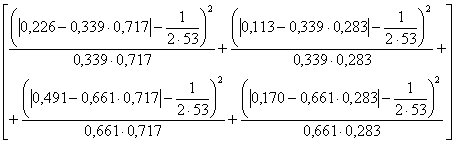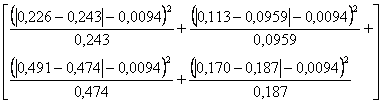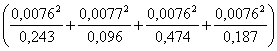CAP III - ANALISI DELLE FREQUENZE

 

 

3.4.   CORREZIONI PER LA CONTINUITA’ IN TABELLE 2 X 2: YATES  E  HABER

 

 

Anche per le tabelle 2 x 2 valgono le stesse condizioni di validità, legate al numero di osservazioni raccolte:

-          il chi quadrato fornisce risultati attendibili con grandi campioni  (N > 100)

-          non è attendibile per campioni eccessivamente ridotti (N < 30).

Quando si debbono confrontare campioni che hanno un numero totale di osservazioni tra 100 e 30, con la formula generale si deve aggiungere 0,5 allo scarto minore e togliere 0,5 allo scarto maggiore.

Nella formula abbreviata, questa correzione per la continuità di Yates comporta una riduzione del valore del chi quadrato, mediante la sottrazione di N/2 al valore assoluto dello scarto tra le due diagonali.

 

Con la correzione proposta da F. Yates nel 1934 (vedi: Contingency tables involving small numbers and the c² test pubblicato su Journal of the Royal Statistical Society Suppl. 1: 217-235), pubblicato ancora nel 1984 (con il titolo Tests of significance for 2 x 2 contingency tables, su Journal of the Royal Statistical Society, Series A, vol. 147, pp. 426- 449 con molti articoli di commento), la formula del chi quadrato per tabelle 2 x 2 diviene:

 

 

Gli effetti della correzione sono relativamente tanto maggiori quanto più basso è il numero di osservazioni. Quando il campione è di grandi dimensioni, la correzione diviene trascurabile. Sulla base di queste osservazioni, alcuni testi come formula abbreviata riportano solamente questa ultima: è utile in campioni con meno di 100 osservazioni e diviene superflua, non comporta alterazioni sensibili, quando il campione è molto grande .

 

Le proposte per la correzione più adeguata sono numerose, come si potrà vedere anche nel test G, dove sono fondate su principi simili. Il dibattito è stato ripreso negli ultimi decenni e nei programmi informatici viene utilizzata anche la correzione proposta da M. Haber nel 1980 (vedi l’articolo A comparison of some continuity corrections for the chi-squared test on 2 x 2 tables, pubblicato su Journal of the American Statistical Association, vol. 75, pp. 510-515) e nel 1982 (The continuity correction and statistical testing, pubblicato su International Statistical Review, vol. 50, pp. 135-144), sviluppando concetti presentati già 40 anni prima, in particolare da  W. G. Cochran nel 1942  (vedi l’articolo The c² correction  for continuity, pubblicato su Iowa State Coll. J. Sci. Vol. 16, pp. 421-436) e  nel 1952 (The c²  test for goodness of fit, pubblicato su Annals of Mathematical Statistics Vol. 23, pp. 315-345).

 

Il metodo di Haber è fondato sul valore atteso (Att._min) minore, identificato ovviamente all’incrocio tra il totale di riga (R_{i min}) minore e il totale di colonna (C_{i min}) minore,

 con

 

Lo scarto in modulo tra questa frequenza attesa e la corrispondente frequenza osservata (Oss.) permette di calcolare 

 =

 

Quando  , si definisce D l’arrotondamento a 0,5 inferiore a

Quando  > , si definisce D = - 0,5.

 

Da D si ricava il c² corretto ()

 =

 con la solita simbologia,

 ricordando

-          che in una tabella 2 x 2 i quattro valori di D sono uguali, cioè gli scarti tra osservati ed attesi sono uguali in valore assoluto,

-          quando  > e quindi D = - 0,5, la correzione di Haber e quella di Yates forniscono lo stesso risultato.

 

ESEMPIO  1 (Correzione di Yates). Per valutare gli effetti di due diserbanti, si confronta il numero di piante cresciute normalmente e di quelle non cresciute nei rispettivi appezzamenti di terreno. Nella zona in cui è stato utilizzato il diserbante A, su un totale di 18 pianticelle presenti 12 sono cresciute e 6 sono seccate; nella zona dove è stato utilizzato il diserbante B,  26 sono cresciute e 9 sono morte.

I due diserbanti hanno effetti significativamente differenti sulla crescita delle pianticelle?

 

Risposta.  Per l’analisi dei dati e l’interpretazione dei risultati è sempre utile riportate i dati dell’esperimento in una tabella 2 x 2.

 

	Piante Cresciute	Piante Non cresciute	Totale
Diserbante A	12	6	18
Diserbante B	26	9	35
Totale	38	15	53

 

Secondo l’ipotesi nulla (H₀), i due diserbanti hanno effetti uguali: le differenze riscontrate sono imputabili al caso.

Secondo l’ipotesi alternativa (H₁), i due diserbanti hanno effetti significativamente differenti.

E’ un confronto tra due campioni indipendenti con un numero di osservazioni (53) che è ritenuto sufficiente per l’uso del test , ma con la correzione di Yates. E’ possibile ricorrere alla formula per il calcolo rapido, apportando la correzione per la continuità.

 

 

Il valore calcolato del chi quadrato con un grado di libertà (0,0682) è particolarmente basso, inferiore a quello tabulato alla probabilità a = 0.05. Con una lettura della tavola dei valori critici più dettagliata, è possibile osservare che esso è inferiore addirittura a quello corrispondente alla probabilità a = 0.90.

Di conseguenza, esiste una probabilità elevatissima di trovare per caso scarti uguali o superiori a quelli riscontrati: non si può rifiutare l’ipotesi nulla, secondo la quale le differenze osservate tra gli effetti dei due diserbanti sono dovute solamente a variazioni casuali.

 

ESEMPIO 2 (Confronto tra correzione di Yates e correzione di Haber). Con lo stesso esperimento dell’esempio precedente, si supponga che il risultato sia stato

 

	Piante Cresciute	Piante Non cresciute	Totale
Diserbante A	15	9	24
Diserbante B	10	16	26
Totale	25	25	50

 

 

I due diserbanti hanno effetti significativamente differenti sulla crescita delle pianticelle?

 

Risposta

Con il metodo di Yates

 

 

 si ottiene un chi – quadrato corretto uguale a 2,003.

 

Con il metodo di Haber,

-          dopo aver individuato il totale di riga minore (24) e il totale di colonna minore (25) si calcola il valore atteso minore (), con i dati dell’esempio

 

 si ottiene = 12,0

-          La differenza in valore assoluto dell’(12,0) con l’Osservato corrispondente (9)

è

 =  =

uguale a 3,0.

-          Poiché l’osservato è minore di 2 volte l’atteso

9 < 2 × 12,0

 con  si utilizza D = 2,5.

Infine con

 =  =

 

 si ottiene un chi–quadrato corretto uguale a 2,003.

In questa condizione il risultato è identico. Nell’altra condizione, ad alcuni autori appare più precisa la correzione di Haber.

Il metodo di Haber è più complesso e lungo di quello proposto da Yates. Ma l’uso dei programmi informatici permette ora di scegliere le misure più sofisticate, ritenute più corrette. In passato, era di estrema importanza anche la semplicità e la rapidità.

 

In un suo articolo dell’anno 1900 (On the criterion that a given system of deviations from the probable in the case of a correlated system of variables in such that it can be reasonably supposed to have arisen from random sampling, Pubblicato sulla rivista Philos. Mag., vol. 50 (5), pp. 157-175), Karl Pearson propone una formula fondata sul calcolo delle proporzioni

 

 

che ingloba anche la correzione per la continuità, dove

 

 

-          p_ij è la frequenza relativa osservata di una casella

-          p_i e p_j è la somma di riga e di colonna delle frequenze relative, per cui il loro prodotto

-          p_i × p_j è la frequenza attesa in ogni casella collocata al loro incrocio e

-          N è il numero assoluto di osservazioni.

 

Riprendendo l’ultima tabella con valori osservati, in cui N = 53, le proporzioni diventano

 

	Piante
	Cresciute	Non cresciute	Totale
Diserbante A	0,226	0,113	0,339
Diserbante B	0,491	0,170	0,661
Totale	0,717	0,283	1

 

e il calcolo del chi quadrato

 

c² = 53 ·

 

c² = 53 ·

 

c² = 53 ·

 

c² = 53 · (0,00024 + 0,00062 + 0,00012 + 0,00031) =  53 · 0,00129 = 0,06837

 

 stima un valore (0,06837) leggermente superiore a quello precedente (0,0682) a causa degli arrotondamenti e soprattutto dell’assenza della correzione per la continuità.

 

Nell’analisi statistica delle tabelle di contingenza, esistono altre convenzioni, oltre quelle ricordate sulla loro impostazione (la causa sulle righe, l’effetto sulle colonne) e sull’indicazione con lettere (a, b, c, d) delle frequenze riportate nelle 4 caselle.

A una associazione si attribuisce

-          segno positivo, quando le frequenze più alte sono nelle due celle della diagonale principale (a - d),

-          segno negativo, quando le frequenze più alte sono nella diagonale secondaria (b – c).

Naturalmente è una pura convenzione, non ha un valore intrinseco. Basterebbe, come è pienamente legittimo trattandosi di dicotomie, invertire la posizione delle righe o delle colonne per invertire anche il segno della associazione.

Come può essere stato dedotto in modo autonomo dallo studente osservando le caratteristiche di una tabella, si ha il massimo di equilibrio tra le modalità di una dicotomia quando a ciascuna è attribuito lo stesso numero di dati (n₁ = n₂; n₃ = n₄). Con un linguaggio più tecnico, si dice allora che la dicotomia ha il massimo della varianza; un altro modo per esprimere lo stesso concetto è che è massima l’aspettativa di errore nell’indovinare se un dato appartiene a una o all’altra categoria.

 

Per evidenziare l’associazione, sia visivamente nei dati, sia con l’analisi statistica, sono importanti altre due caratteristiche nella distribuzione dei dati:

-          i totali marginali delle due dicotomie sono equilibrati,

-          le frequenze sono maggiori lungo una diagonale.

Quando si confrontano le frequenze osservate con quelle attese, si ha

-          associazione positiva quando la frequenza osservata è maggiore di quella attesa,

-          associazione negativa quando quella osservata è minore di quella attesa.

Nella letteratura francese (vedi di J. P.  Benzécrì del 1973 il testo L’analyse des donnés, edito da Dunod, Paris) si parla di

-          attrazione tra la modalità riportata nella riga e quella nella colonna che individuano la casella, quando la frequenza osservata è significativamente maggiore di quella attesa,

-          repulsione quando la frequenza osservata è significativamente minore di quella attesa