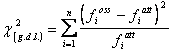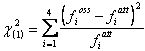CAP III - ANALISI DELLE FREQUENZE

 

 

3.3.  LE TABELLE DI CONTINGENZA  2 X 2 (FOURFOLD TABLES)

 

 

Quando si confrontano le frequenze di risposte binarie in due campioni indipendenti, è utile costruire una tabella a doppia entrata, chiamata tabella di contingenza (dal latino contingo, vengo a contatto, in quanto i risultati sono prodotti dall’incontro di due serie di fattori o caratteristiche).  Per ognuno dei due gruppi, deve essere riportato il conteggio di risposte binarie, quali il numero di successi e quello di insuccessi oppure di quelli che presentano la caratteristica X e di quella alternativa Y.

Trattandosi del confronto tra due differenti campioni con risposte alternative di tipo binario, la tabella costruita con i dati sperimentali è chiamata  tabella 2 x 2 (in inglese, fourfold tables).

 

Il test chi quadrato permette di verificare se le proporzioni di successi e di insuccessi nei due gruppi sono indipendenti dal trattamento al quale sono sottoposti oppure se esiste associazione tra essi.

Per esempio, si supponga di voler verificare se vivere in una zona ad alto inquinamento atmosferico incide sulla frequenza di malattie polmonari. A questo scopo, in una zona con tassi elevati d’inquinamento e in una con livelli molto bassi, sono stati analizzati alcune decine d’individui residenti da alcuni anni, contando quanti sono coloro che presentano malattie polmonari.

 

DISTRIBUZIONE OSSERVATA IN TABELLA 2 X 2

 

 

 

Nei testi di statistica, non esiste uniformità su come costruire la tabella. La convenzione qui seguita è quella proposta da H. Zeisel  nel 1947 (nel volume Say it with figures, Harper & Row, New York; tradotto in italiano nel 1968, in Ditelo coi numeri, Marsilio, Padova), che riporta

-  le due modalità della variabile casuale sulle righe,

-  le due modalità della variabile effetto sulle colonne.

 

La tabella riporta i risultati dell’analisi epidemiologica. Con questi dati, si può concordare con la teoria enunciata?

Il test chi quadrato utilizza i casi effettivamente contati, non le frequenze relative o percentuali, anche se su di esse vengono formulate le ipotesi.

Un’altra convezione, in questo caso generalmente seguita, suggerisce di indicare le frequenze riportate in ognuna delle 4 celle con le lettere minuscole a, b, c, d, (con la disposizione utilizzata nella tabella precedente). Il totale generale dei dati è indicato con la lettera maiuscola N.

 

Per comprendere la procedura del chi quadrato in tabelle 2 x 2, è bene seguire alcuni passaggi logici.

1-       Se fosse vera l’ipotesi nulla (H₀: vivere in una zona ad alto inquinamento atmosferico non cambia la frequenza di malattie polmonari, rispetto ad una zona a basso inquinamento), la frequenza relativa di persone con malattie polmonari nei 2 gruppi a confronto sarebbe uguale; le differenze riscontrate sarebbero da interpretare come variazioni casuali.

2-       La stima migliore di questa frequenza relativa o incidenza percentuale, valida nella condizione che l’ipotesi nulla sia vera, è data dalla somma delle persone con malattie polmonari nei 2 gruppi ( a + c   cioè 32 + 13 = 45) rapportate al numero totale di persone osservate:

 (a + c)/N   cioè   45 / 150 = 0,3.

3-       Considerando che i due campioni a confronto hanno un numero differente di osservazioni, sempre nel caso che l’ipotesi nulla sia vera,

-          nel primo campione (che è composto da 80 individui) dovremmo aspettarci di trovare 24 persone (0,3 x 80 = 24 ) con malattie polmonari e

-          nel secondo campione (composto da 70 individui) di trovarne 21 (0,3 x 70 = 21).

 

I quattro valori attesi possono essere presentati in una tabella 2 x 2, come i valori osservati.

Per la sua costruzione, è utile riportare dapprima i 4 totali marginali ed il totale generale.

Successivamente, si calcola ognuno dei 4 valori attesi, moltiplicando il totale di riga per il totale di colonna, diviso per il totale generale:

a = n₁ x n₃ / N;

b = n₁ x n₄ / N;

c = n₂ x n₃ / N

d = n₂ x n₄ / N

 

DISTRIBUZIONE ATTESA IN TABELLA 2 X 2

 

 

 

E’ utile osservare come non sia necessario calcolare tutte e quattro le frequenze attese.

Poiché i totali marginali sono già fissati, è sufficiente calcolare uno solo dei 4 valori attesi, qualunque esso sia, per poter dedurre gli altri 3 per differenza.

Per esempio,

-  una volta calcolato 24 per la casella a

-  è ovvio che nella casella b possiamo trovare solo 56, perché il totale della riga è 80, e

-  nella casella c possiamo trovare solo 21, perché il totale è già prefissato in 45;

-  da uno qualsiasi di questi 3 dati già scritti deriva che la casella d può riportare solamente 49, affinché i vari totali marginali possano coincidere.

Il ragionamento non varia, partendo da qualsiasi casella.

Queste considerazioni aiutano a comprendere perché una tabella attesa 2 x 2 ha  solamente 1 grado di libertà. E’ possibile anche un’altra spiegazione, che assume molta importanza in statistica e che sarà costante ripresa nell’analisi della varianza, per capire come

-  i gdl sono legati alla quantità di informazione raccolta (numero di dati) e

-  ogni informazione ricavata da essi ne abbassa il numero.

Per stimare l’atteso di ogni casella, noi abbiamo bisogno di 3 informazioni:

-  il totale di riga,

-  il totale di colonna,

-  il totale generale (N).

Gli altri 2 totali parziali sono derivabili da questi tre e non rappresentano una reale informazione aggiuntiva. Ad esempio, se conosco che il totale generale è 150 e il totale della prima riga è 80, so anche che il totale della seconda riga è 70. Nello stesso modo, se so che il totale della prima colonna è 45, so anche che il totale della seconda colonna è 105.

Poiché i dati sono 4, ne deriva che i gradi di libertà è uno solo (gdl = 4 – 3 = 1).

 

Colui che propose questo metodo per primo, Karl Pearson, attribuì erroneamente un numero maggiore di gradi di libertà. Fu il suo allievo R. A. Fisher, allora molto giovane, che mostrò il procedimento esatto.

Stimata la distribuzione attesa  nell’ipotesi che sia vera l’ipotesi nulla, dalle differenze tra osservato ed atteso si calcola il valore del chi quadrato, mediante

 la formula generale già presentata:

dove:

-  f_i^oss = frequenza osservata   i-esima

-  f_i^att  = frequenza attesa   i-esima

 ed estendendo la sommatoria (å) ai dati di tutte quattro le caselle.

 

Con i dati dell’esempio

c²₍₁₎  =  (32 - 24)² / 24 + (48 - 56)² / 56 + (13 - 21)² / 21 + ( 57 - 49)² / 49 =

=     2,666 +  1,143  +  3,048  +  1,306  =   8,163

 

 si ottiene un valore del chi quadrato, con 1 gdl,  uguale a 8,163

 

La tavola sinottica del  c²₍₁₎ riporta

-  il valore critico di 3,84 alla probabilità a = 0.05 e

-  il valore critico di 6,64 alla probabilità a = 0.01.

Il valore calcolato (8,163) è superiore sia a quello della probabilità 0.05 che di quella 0.01; di conseguenza, si rifiuta l’ipotesi nulla ed implicitamente si accetta l’ipotesi alternativa.

Con i dati dell’esempio, lo statistico arriva alla conclusione che, con probabilità a < 0.01 di commettere un errore (cioè che sia vera l’ipotesi nulla), la percentuale di persone con malattie polmonari è significativamente differente nei due gruppi a confronto.

 

Questa procedura è utile per capire il reale significato del test c² in tabelle di contingenza 2 x 2. Inoltre, il confronto tra distribuzione osservata e distribuzione attesa mostra in quali caselle si trovano le differenze più importanti. Nell’esempio, tale confronto mostra che le persone con malattie polmonari (riportate nella tabella delle frequenze osservate) sono più frequenti nella zona con maggior inquinamento e sono meno frequenti nella zona senza inquinamento atmosferico, rispetto all’ipotesi nulla che esse abbiano la stessa frequenza percentuale (riportate nella tabella delle frequenze attese).

 

Si può ottenere lo stesso risultato ed evitare il lungo calcolo delle frequenze attese, con il ricorso alla formula per il calcolo rapido del chi quadrato per le tabelle di contingenza 2 x 2

 

 

dove, con la simbologia e i valori riportati nella tabella osservata

 

 

 

 

-  a, b, c, d sono le frequenze osservate nei due campioni a confronto,

-  n₁, n₂, n₃, n₄ sono i totali marginali,

-  N è il totale generale di osservazioni.

 

Il calcolo, con i dati sperimentali dell’esempio precedentemente utilizzato, fornisce

c²₍₁₎ = [ (32 x 57 - 48 x 13)² x  150 ] / (80 x 70 x 45 x 105)

c²₍₁₎ = (1824 - 624)² x 150 / 26460000 = 1440000 x 150 / 26460000 = 8,163

 un c²₍₁₎   = 8,163.

 

E’ un valore identico a quello calcolato in precedenza, con la formula estesa.

L’equivalenza tra le due formule potrebbe essere dimostrata con una serie di passaggi matematici; ma per l’utente della statistica applicata è sufficiente ricordare le due formule, da usare nelle differenti condizioni.

 

 

ESEMPIO. Si vuole controllare l’effetto di due tossici su due gruppi di cavie. Il tossico A, somministrato a 70 animali, ha causato la morte di 22 individui (e naturalmente 48 sono sopravvissuti), mentre il tossico B in un esperimento con 50 animali ha causato la morte di 24 individui. Si vuole sapere se i due tossici hanno gli stessi effetti sulla mortalità o sopravvivenza (H₀); oppure se i due tossici hanno probabilmente effetti letali differenti (H₁).

 

Per meglio evidenziare i dati del problema, i conteggi devono essere riportati in una tabella a due entrate

 

	Cavie
	Morte	Sopravv.	Totale
Tossico A	22	48	70
Tossico B	24	26	50
Totale	46	74	120

 

 

che fornisce in modo chiaro tutte le informazioni utili.

Nella condizione che l’ipotesi nulla sia vera (i farmaci hanno lo stesso effetto e le variazioni riscontrate sono dovute solo al caso), le frequenze attese possono essere calcolate dai totali: se i due tossici producessero lo stesso effetto, in ognuno dei due gruppi morirebbero il 38% (46/120) e sopravviverebbero il 62% (74/120), ovviamente rapportati ai totali dei due gruppi di 70 e 50 animali.

E’ quindi possibile costruire una tabella delle frequenze attese.

 

Dapprima, si riportano i totali marginali e quello generale; successivamente, da essi si stimano i dati attesi in ognuna delle 4 caselle con la relazione

che devono essere collocati nella tabella 2 x 2:

 

	Cavie
	Morte	Sopravv.	Totale
Tossico A	26,83	43,17	70
Tossico B	19,17	30,83	50
Totale	46	74	120

 

E’ importante osservare che una volta che è stata riportata la prima frequenza attesa

 

 

le altre possono essere ottenute anche per differenza dai totali rispettivi di riga o di colonna:

 

 

L’ultima frequenza attesa (30,83) può essere calcolata sia dai suoi due totali marginali che dal totale generale.

La tabella di contingenza  ha un solo valore che può assumere qualsiasi valore, quindi ha 1 gdl.

 

Dal confronto tra tabella dei dati osservati e tabella dei dati attesi si può calcolare il valore del  mediante la formula generale:

 

Con i dati dell’esempio

 

 

 

 si ottiene un valore uguale a 3,42.

Oppure, ricordando la simbologia,

 

 

 e la formula abbreviata

 

 è possibile arrivare al risultato in modo molto più rapido

 

 

 ottenendo un chi quadrato uguale a 3,39.

I due risultati 3,42 e 3,39 non coincidono perfettamente anche per effetto degli arrotondamenti, ma risultano sempre molto simili.

La formula abbreviata è da preferire per il calcolo (richiede meno tempo), mentre la formula generale è di aiuto nell’interpretazione dei risultati (mediante il confronto tra frequenze osservate e frequenze attese).

Nella tabella dei valori critici della distribuzione  per 1 grado di libertà alla probabilità 5% è riportato 3,84; il valore del chi quadrato che è stato calcolato è inferiore. Di conseguenza, la probabilità che le differenze riscontrate tra i due tossici siano dovute al caso è da ritenersi elevata: non si può respingere l’ipotesi nulla.

In termini biologici, con questi dati non è possibile dimostrare che i due tossici abbiano effetti significativamente differenti.