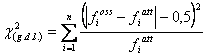CAP III - ANALISI DELLE FREQUENZE

 

 

3.2.   CONDIZIONI DI VALIDITA’ DEL  E CORREZIONE DI YATES

 

 

Fissata la probabilità, il valore critico del chi quadrato è totalmente determinato dai suoi gradi di libertà e quindi dal numero di gruppi (sulla relazione tra numero di gruppi e gradi di libertà si tornerà nel prosieguo del capitolo).

Il numero di osservazioni, in totale ed entro ogni gruppo, sono a questo riguardo ininfluenti. Eppure, anche senza esperienza di statistica, appare logico pensare che il risultato sia tanto più attendibile quanto più elevato è il numero di osservazioni nell’esperimento.

 

Nel test c² il numero di osservazioni, sia in totale che entro ogni classe, determina la condizione essenziale di validità.

Il  è valido solamente quando è applicato a grandi campioni.

 

Definito il principio, sotto l’aspetto pratico esiste scarsa concordanza su quando un campione possa essere universalmente ritenuto di grandi dimensioni. La maggioranza dei testi di statistica pone limiti, seppure non definiti in modo chiaro ed universale, con i quali si possono formare 3 classi di “credibilità” o validità del test.

 

1- Il test è valido quando il numero totale di osservazioni è superiore a 100; tuttavia, più recentemente, vari autori ne pretendono un numero maggiore, circa 200; altri, ancora più rigorosi, ne chiedono addirittura 500.

 

2 - Il test è meno attendibile ed ha bisogno di una correzione, quando il numero di osservazioni è tra 200 (o 100) e 30 circa. E’ detta correzione di Yates, in quanto proposta da F. Yates nel 1934 (con l’articolo “Contingency tables involving small numbers and the test c², pubblicato sulla rivista inglese Journal of the Royal Statistical Society, Suppl. 1, pp. 217-235). (Frank Yates inglese, nato nel 1902 e morto nel 1994, assistente di Fisher nel 1931 e direttore del Dipartimento di Statistica a Cambridge dal 1933 al 1968).

 

3 - Il test perde ogni attendibilità quando il numero di osservazioni è inferiore a 30; diversi autori pongono questo limite a 40, mentre altri tendono ad abbassarlo fino a 25, molto raramente fino a 20.

Il motivo è che, con così pochi dati, le variazioni casuali diventano così ampie da non poter mai rifiutare l’ipotesi nulla con una probabilità ragionevolmente bassa, per quanto distanti possano essere le frequenze osservate e quelle attese.

 

A questa condizione sul numero totale di dati è necessario aggiungerne una seconda:

-   il numero di frequenze attese entro ogni classe non deve essere minore di 5.

Anche su questo secondo criterio non esiste unanimità. Alcuni testi abbassano questo limite fino a 4, molto raramente fino a 3. Altri ancora pongono questi limiti considerando anche il numero di classi: ritengono accettabile il risultato, quando non più di 2-3 gruppi abbiano meno di 5 osservazioni attese. Tuttavia, la maggioranza degli studiosi definisce queste ultime frequenze come insufficienti.

E’ quindi utile ricordare che, quando ha un numero abbastanza alto di gradi di libertà, il chi quadrato è meno sensibile agli errori determinati da frequenze attese piccole.

 

Con questi doppi limiti, che interessano

-  sia il numero totale di osservazioni

-  sia la loro frequenza entro ogni gruppo,

 anche il numero di suddivisioni che è possibile considerare è ovviamente limitato e dipende dal numero totale di dati. Per esempio, con un totale di 50 osservazioni non è possibile avere più di 10 gruppi, perché in una distribuzione uniforme la media attesa sarebbe di 5 e, in una distribuzione non uniforme, in alcuni gruppi le frequenze attese sarebbero necessariamente ancora inferiori a tale valore limite.

 

Per campioni di dimensioni inferiori a 200 (100) ma superiori a 30, si deve apportare la correzione di Yates o correzione per la continuità.

E’ una procedura uguale a quella illustrata per l’uso della normale in distribuzioni binomiali con campioni di grandi dimensioni. Per passare da una distribuzione discreta, come è un conteggio, ad una distribuzione continua, come sono la normale e la distribuzione c², con un numero intero (ad esempio, X = 12) si deve intendere non la misura precisa (come può essere una lunghezza di cm. 12,000 o un peso di g. 12,000), ma lo spazio unitario compreso tra X - 0,5   e   X + 0,5.

 

Per effettuare questa correzione richiesta dal passaggio da una misura discreta a una continua, è necessario, prima dell'elevamento al quadrato

-  sottrarre 0,5 ad ogni scarto in valore assoluto.

Si ottiene una riduzione del valore del chi quadrato rispetto alla procedura senza correzione. E’ un risultato cautelativo, con il quale è meno probabile rifiutare l'ipotesi nulla.

Successivamente si vedranno altre correzioni, tra le numerose proposte in letteratura. Questa rimane la più diffusa, è riportata su quasi tutti i testi di statistica elementare o di base. A livelli più sofisticati è criticata, in quanto troppo cautelativa: ridurrebbe eccessivamente il valore del chi quadrato, e quindi renderebbe troppo difficile rifiutare l'ipotesi nulla. Nel capitolo successivo, si dirà che determina un test poco potente.

 

ESEMPIO.  In un conteggio sulla distribuzione di una specie vegetale, in 3 appezzamenti della stessa superficie sono state contate rispettivamente 15, 21 e 24 unità. Verificare se la distribuzione osservata è in accordo con la distribuzione uniforme, cioè di 20 in ogni classe.

 

Risposta

-          Senza correzione, il valore del  è

 

 

-          Con la prima correzione di Yates diventa

 

 

-          Con la seconda correzione diventa

 

 

Al posto di 2,1 il valore corretto del c² diminuisce a 1,925 con un metodo e 1,6375 con l’altro.

La correzione di Yates o per la continuità ha sempre l'effetto di ridurre il valore del .

Teoricamente, dovrebbe essere applicata sempre, anche a grandi campioni. Ma quando il numero di dati diventa alto, i suoi effetti diventano nulli o almeno trascurabili.

 

Il suo merito principale è quello di rendere le conclusioni più prudenti, in modo tanto più sensibile quanto più basso è il numero di osservazioni. Con la correzione, si abbassa la probabilità di rifiutare l’ipotesi nulla. Infatti, quando il numero di osservazioni è limitato, le variazioni casuali tendono ad aumentare la loro incidenza relativa.

Gli scarti tra frequenze osservate e frequenze attese non risentono solamente delle differenze realmente esistenti tra le due distribuzioni a confronto, ma anche delle variazioni casuali. In questa ottica, si può intuitivamente comprendere come il test  non abbia validità per rifiutare l’ipotesi nulla, quando il numero di osservazioni è troppo ridotto. Con un termine più tecnico si dice che il test è troppo poco potente, poiché le variazioni casuali tendono ad essere così elevate, da non permettere più di evidenziare in modo significativo l’esistenza di differenze reali tra osservato ed atteso.

 

Per indicare l’effetto delle variazioni casuali in un campione di dimensioni troppo ridotte, in alcuni testi si usa il termine rumore o rumore bianco (white noise), per distinguerlo dalle altre cause che possono generare variabilità (rumore). Quando il numero di osservazioni è basso, il “rumore” (la variabilità casuale) diventa così forte da non permettere di evidenziare le reali tendenze di fondo delle distribuzioni.

Tuttavia, non vi è accordo generale sull’utilità di questa correzione; in alcuni testi non viene né citata né riportata, appunto perché riduce la potenza del test. Per risolvere ugualmente il problema di verificare l’accordo tra una distribuzione osservata e una distribuzione attesa sono stati proposti altre metodologie, come il test di Kolmogorov-Smirnov, il metodo esatto di Fisher, il test G che saranno presentati nei paragrafi successivi.