LA REGRESSIONE LINEARE MODELLO II  E LEAST-PRODUCTS.

IL CONFRONTO TRA DUE METODI QUANTITATIVI.

 

 

 

24.7  LA REGRESSIONE LINEARE E IL TEST PER L’EQUIVALENZA TRA DUE METODI ANALITICI DI PASSING-BABLOK

 

 

Nella ricerca di laboratorio e nelle applicazioni industriali, è sempre forte l’esigenza di ridurre i tempi e i costi delle analisi quantitative, con metodi nuovi e meno costosi. Nelle determinazioni chimiche e cliniche, sovente si propongono metodi più raffinati o più rapidi oppure basati su un principio differente, per valutare la quantità di principio attivo presente. Si tratta di decidere se i risultati sono equivalenti e quindi se i due metodi di misurazione sono uguali.

Per questi problemi di chimica analitica e chimica clinica, H.  Passing e W. Bablok  con gli articoli

-  del 1983 A new biometrical procedure for testing the equality of measurements from two different analytical methods. Application of linear regression procedures for method comparison studies in clinical chemistry. Part I. (pubblicato sulla rivista Journal of Clin. Chem. Clin. Biochem., Vol. 21, pp.: 709 - 720),

-  del 1984 Comparison of several regression procedures for method comparison studies and determination of sample size. Application of linear regression procedures for method comparison srudies ib clinical chemistry. Part II (pubblicato sulla rivista Journal of Clin. Chem. Clin. Biochem., Vol. 22, pp.: 431 - 445),

 propongono  un test statistico per verificare se i due metodi forniscono le stessa misura.

Il problema è da essi presentato (1983, pag. 710) in questi termini:

-  There are 2 different methods (instruments) which measure the same chemical analyte in a given medium (e.g. serum, plasma, urine, …). The question is: Do the methods measure the same concentration of the analyte or is there a systematic difference in the measurements? (For simplicity, we only refer to concentration but our statements are also valid for any other quantity.)

 

Quando, in campioni indipendenti estratti da una popolazione, un dato analita è misurato con valore  e  per ogni campione , si ottengono

 e

 dove

 -   e  sono i valori stimati dalla retta per lo stesso campione ,

-    e    sono gli errori delle due misure.

Con questa impostazione logica,

-  ognuno dei due metodi ha il suo valore atteso  e   per il campione

-  e se esiste una relazione strutturale tra i due metodi, essa può essere descritta dalla generica equazione lineare

 

 

 Al momento della pubblicazione del primo articolo di Passing e Bablok (anno 1983), la relazione strutturale tra i due metodi era ricavata con 4 metodi statistici:

1 - la regressione lineare

2 - la regressione lineare

 

3 - la procedura di Deming, che Passing e Bablok chiamano principal component analysis, 

 

4 - la standardized principal component analysis.

 

Essi hanno condizioni di validità differenti e forniscono rette differenti (già illustrate nei paragrafi e nei capitoli precedenti).

 

Nella impostazione concettuale di Passing e Bablok, per un vera analisi di comparabality tra due metodi mediante la regressione lineare, è necessario raggiungere quattro obiettivi:

1 –  calcolare l’intercetta  e il coefficiente angolare ;

2 –  verificare con un test se sussistono le assunzioni per la linearità.

Solamente dopo aver dimostrato il punto due,

3 –  verificare l’ipotesi  = 1,

4 -  verificare l’ipotesi  = 0.

I due ultimi test sono fondati sul concetto che, se i due metodi sono equivalenti e senza errori, i punti dovrebbero collocarsi lungo la retta che ha  = 1 e  = 0. Ovviamente occorre considerare la presenza di errori random, ma scoprire errori costanti (differenze sistematiche) tra i due metodi.

 

Il metodo di Passing e Bablok non ha una dimostrazione teorica, ma solo verifiche empiriche fondate su simulazioni. E’ utilizzato su campioni grandi, che hanno varie decine di coppie di osservazioni, per cui già nella presentazione da parte degli autori sono stati proposti programmi informatici, da essi scritti in PASCAL  e  BASIC, che rendono possibile e semplice l’applicazione del metodo.

Da alcuni anni, questi programmi per il test di equivalenza tra due metodi sono rintracciabili nelle librerie informatiche per analisi cliniche e chimiche, in quanto la procedura ora è ritenuta la prassi corretta per valutare l’equivalenza tra due metodi.

 

I concetti di base della regressione lineare di Passing e Bablok sono simili a quelli della retta non parametrica di Theil (vedi capitolo relativo), che ovviamente sviluppò il metodo senza pensare al confronto tra metodi. Quindi anche la regressione di Passing e Bablok è classificata tra i metodi non parametrici.

Nell’articolo del 1983, i due autori (a pag.713) scrivono: The basic concept of our regression procedure is due to Theil who developed this idea without reference to the problem of method comparison.

 

La differenza concettuale più importante tra questi due metodi  è che mentre la retta non parametrica di Theil assume, come avviene per la retta parametrica least-squares, che la  sia fissa, Passing-Bablok assumono (come evidenziato all’inizio del paragrafo) che i due metodi abbiano lo stesso tipo di errore (non che esso abbia la stessa dimensione, nelle misure ottenute con i due metodi).

Quindi differenziano il loro procedimento da quello di Theil, introducendo un parametro , che misura il numero di coefficienti angolari collocati dalle due parti rispetto a  = 1.

Successivamente, costruiscono l’intervallo di confidenza del coefficiente angolare  calcolato, per il rischio  o la probabilità  prestabiliti (quasi sempre il 95%),

-  sulla base del numero di osservazioni e utilizzando la distribuzione normale (come in quasi tutti i test non parametrici fondati sui ranghi, poiché la loro distribuzione diventa rapidamente normale).

 

Con logica simile a quella utilizzata per il coefficiente angolare, la stima dell’intercetta  richiede che una metà dei punti sia collocata sopra la retta e l’altra metà sotto.

Il successivo test di linearità prende in considerazione

-  la posizione dei punti (valori osservati)  rispetto alla loro proiezione sulla retta (valori attesi).

Con un test analogo e con gli stessi valori critici del test di Kolmogorov-Smirnov, si valuta l’accordo tra la distribuzione osservata e quella attesa.

 

Si passa quindi al test per la verifica dell’ipotesi nulla  = 1, che è effettuata ricorrendo all’intervallo di confidenza di .  L’ipotesi  = 1 è accettata, se il valore 1 è compreso nell’intervallo. Il rifiuto dell’ipotesi nulla dimostra che un metodo fornisce un valore non uguale all’altro, ma al massimo proporzionale. (This hypothesis is accepted if the confidence interval for  contains the value 1. If the hypothesis is rejected, then it is concluded that  is significant different from 1 and there is at least a proportional difference between the two methods.)

 

In modo analogo, è verificata l’ipotesi nulla  = 0.

L’ipotesi è accetta, se 0 è compreso nell’intervallo.

Se si rifiuta l’ipotesi nulla, tra i due metodi esiste almeno una differenza costante. (If the hypothesis is rejected, then it is concluded that  is significant different from 0 and both methods differ at least by a constant amount.)

 

Infine la conclusione.

Se sono accettate entrambi le ipotesi  = 1  e    = 0, si può inferire che

-   =

-  e quindi i due metodi sono identici.

 

In un programma informatico standard, i risultati delle analisi statistiche e dei test vengono presentati mediante due grafici:

- il diagramma di dispersione dei valorie  rappresentati da punti, nel quale sono riportate la retta calcolata (eventualmente anche quella teorica con  = 1 e  = 0, per meglio evidenziarne le differenze o l’uguaglianza) e i due intervalli di confidenza, di solito alla probabilità del 95%;

- il plot dei residui, rispetto alla retta calcolata che viene rappresentata come una media

 

Inoltre sono fornite le statistiche:

- dimensione del campione o numero di coppie di dati

 e, per o per ogni variabile o metodo,

- valore massimo e minimo, media, mediana, deviazione standard dei valori e errore standard della media.

Relativamente ai parametri della retta, sono riportati:

-  il valore dell’intercetta  e del coefficiente angolare , entrambi con il loro intervallo di confidenza al 95%.

 

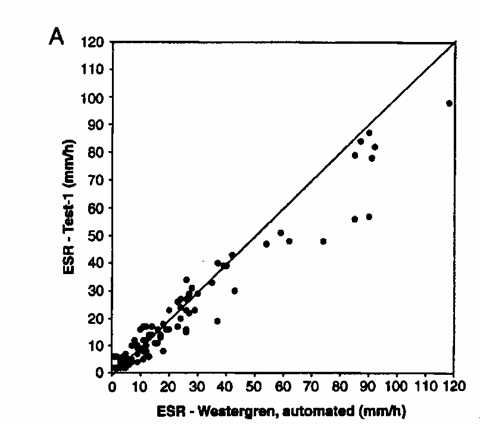
ESEMPIO (TRATTO DA CLINICAL CHEMISTRY). Come dimostrazione della presentazione di un’analisi della regressione effettuata con il metodo di  Passing-Bablok, sono riportate le due figure tratte dall’articolo di Niels de Jonge e alii nell’anno 2000 Erythrocyte Sedimentation Rate by the Test-1 Analyzer (pubblicato in Letters della rivista Clinical Chemistry Vol. 46, No.6,  pp.: 881 - 882).

L’analisi

- della intercambialità di due metodi analitici (Automated Westergren method di riferimento e un test manuale rapido, chiamato Test-1),

 con la quale si vuole verificare

- se il test metodo manuale, più rapido, può sostituire validamente il tradizionale metodo automatico di Westergren, per valutare l’Erythrocyte Sedimentation Rate o ESR (in mm/h),

 è presentata con i seguenti dati:

 

1 -  le dimensioni del campione:  = 105

2 –  il coefficiente di correlazione di Pearson: 

3 -  la retta di regressione:

 

4 - il coefficiente angolare  con  l’intervallo di confidenza al 95% : 0,86 - 0,97

(quindi, seppure di poco, esclude il valore  )

 

5 - l’intercetta  con l’intervallo di confidenza al 95% :  -0,87 - 0,29

(quindi include il valore  )

 

6 – la deviazione standard della misura  (metodo manuale), sulla misura  (metodo di riferimento):  = 5,06

 

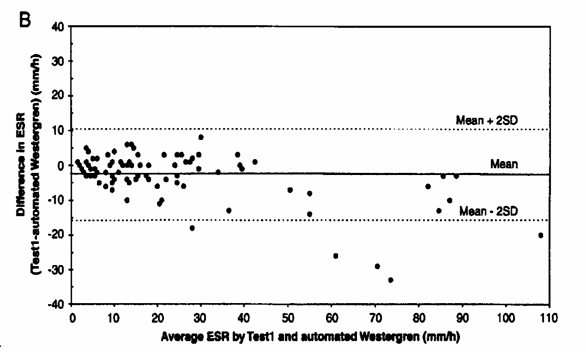
7 -  il plot di Bland-Altman, nel quale in ordinata si legge:

-  la media delle differenze tra le due serie di valori:  –2,7;

-  il valore delle differenze calcolate per ogni coppia di valori è compreso tra il massimo di +8 e il minimo di –33;

-  i limiti al 95% della media delle differenze  (con 2DS = 13,2) sono +10,3 e –15,7.

 

Dall’analisi di questi risultati sono tratte le seguenti conclusioni:

 

 

 

 

 

1 – il test di Passing Bablok evidenzia che il test manuale, chiamato Test-1, offre una determinazione rapida di ESR, con una variabilità tra i due metodi che è accettabile e con una buona correlazione con il tradizionale metodo Westergen (acceptable intraassay variability and good correlation with traditional method);

 

2 – il test di Bland-Altman mostra che l’errore sistematico (bias) e le differenze massime  dell’accordo (agreement limits) tra i due metodi sono delle stesse dimensioni di quelli rilevati con altri metodi.

 

Si arriva alla conclusione finale che, seppure con l’aiuto dell’informazione fornita da vari test, è il giudizio del clinico esperto il criterio fondamentale che permette di dichiarare

-   accettabile l’errore commesso con il metodo nuovo,

-   e che quindi esso può sostituire validamente il metodo precedente.

Ovviamente colui che giudica deve porre particolare attenzione al differente significato dei parametri  e  nella regressione di Passing-Bablok:

-   dipende da un errore analitico costante, un errore di specificità, definita come l'abilità di un metodo a misurare solamente quello che si intende misurare;

-   è determinato da un errore proporzionale costante, un errore di calibrazione, derivante dalla relazione reale che esiste tra i due strumenti o metodi.