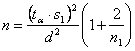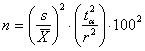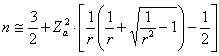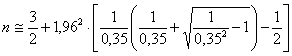IL DISEGNO SPERIMENTALE:

CAMPIONAMENTO, PROGRAMMAZIONE DELL’ESPERIMENTO E POTENZA

 

 

23.6.  STIME PRELIMINARI APPROSSIMATE DELLE DIMENSIONI DEL CAMPIONE E DELLA POTENZA DEL TEST, NELLA RICERCA BIOLOGICA E AMBIENTALE

 

 

Un altro problema pratico di rilevante importanza nella programmazione di una ricerca sono le dimensioni () del campione. L’argomento è già stato affrontato in varie parti del testo. Più esattamente

-  nella stima della potenza di un test e del rischio b, con la distribuzione normale,

-  nella stima della potenza di un test e del rischio b, con la distribuzione t di Student,

-  nell’uso delle curve di potenza, nell’ANOVA.

Inoltre, per alcuni test non parametrici, è stato presentato il metodo specifico. In modo schematico, quanti dati raccogliere () dipende

-  dalle caratteristiche del test che si intende utilizzare,

-  dal tipo di scala con il quale è stata misurata la variabile utilizzata,

-  dalla forma di distribuzione dei dati.

 

Quando si pianifica una ricerca, spesso è utile avere un’idea preliminare, approssimata ma corretta, del numero minimo () di dati che è necessario raccogliere, senza aver già acquisito una conoscenza più approfondita sull’argomento. Per una valutazione rapida del numero di dati necessari, in letteratura e nei testi delle varie discipline sono proposti diversi metodi. Sono stime che successivamente possono essere corrette; ma che non si allontanano molto dai risultati che si ottengono con i metodi più precisi, fondati su basi teoriche più solide, ma più complessi, che sono già stati proposti.

Alcuni di questi metodi rapidi, presentati in particolare per le discipline ambientali e per l’analisi di popolazioni, ma estensibili a molte altre discipline biologiche, sono illustrati sinteticamente nel volume di Charles J. Krebs del 1999, Ecological Methodology (2^nd ed.  Benjamin/Cummings, Addison Wesley Longman, Menlo Park , California, X + 620 p.).

 

Come prima informazione, la risposta alla domanda “quanti dati servono?” esige che sia dichiarato lo scopo per cui  il campione di dati è raccolto. Schematicamente, nei casi più semplici, un campione di dati serve per

-  calcolare una media,

-  confrontare due medie,

-  stimare la varianza, sempre nel caso di misure con scale a intervalli o di rapporti;

-  calcolare una proporzione o percentuale, nel caso di risposte qualitative o categoriali.

 

La seconda informazione necessaria è il livello di precisione, con cui si vuole conoscere il parametro indicato oppure la probabilità a di commettere un errore. La precisione del parametro può essere espressa

-  con una misura relativa, come la percentuale dell’errore accettato rispetto alla media,

- in valore assoluto, come la distanza massima tra la media del campione e quella reale o della popolazione,

-  mediante l’intervallo di confidenza, che permette di derivare con facilità il valore assoluto dello scarto massimo accettato (lo scarto tra un limite e la media).

 

Il terzo gruppo di informazioni riguarda i parametri che sono presi in considerati nella formula proposta e la varianza.

Nella condizione che i dati siano distribuiti in modo normale, almeno approssimativamente, una stima approssimata della dimensione minima () del campione

 è ricavabile con

 dove

-  d  = errore massimo assoluto dichiarato

-  s  = deviazione standard, misurata su un campione precedente o con uno studio pilota

-  t = il valore per gdl n-1 e probabilità a; in pratica con a = 0.05 bilaterale, come richiesto di norma nell’approssimazione di una media campionaria a quella reale, t = 2, se il campione è di dimensioni superiori alle 20 unità.

 

ESEMPIO 1. Alcune misure campionarie della concentrazione di principio attivo hanno dato una  media  = 25  e una deviazione standard  = 11 Quanti dati raccogliere, per una media campionaria che non si allontani dal valore reale di una differenza massima ?

 

Risposta. Con

 si ottiene una stima di circa 54 dati

L’informazione utile è la differenza (d), non la media ().

 

Se l’errore è stato espresso in termini relativi o è stato fornito l’intervallo di confidenza, per il calcolo di n questa informazione deve essere trasformata in una differenza massima (d), espressa in valore assoluto.

 

In alcune situazioni, in particolare se il fenomeno è nuovo, non è possibile avere una stima della varianza (s²) o della deviazione standard (s), mentre è facile conoscere l’intervallo di variazione, cioè la differenza tra il valore massimo e il valore minimo. Ad esempio, solo gli esperti del settore possono conoscere la varianza o la deviazione standard dell’altezza in ragazzi di 20 anni; ma tutti possono stimare come accettabile, nel loro gruppo di amici, un campo di variazione di 30 cm, tra il più basso (circa 160) e il più alto (circa 190 cm).

Una legge empirica molto generale riportata in vari testi e già citata, fondata esclusivamente sulla pratica, permette di calcolare

 

 per mezzo di un fattore di conversione del campo di variazione in deviazione standard, ritenuto generalmente uguale a 0,25 (1/4).

Ma, come già riportato nel primo capitolo sulla statistica descrittiva, il campo di variazione aumenta al crescere della numerosità del campione. Pertanto, come da W. J. Dixon e F. J. Jr. Massey nel loro testo del 1983 Introduction to Statistical Analysis (4^th  ed. McGraw-Hill, New York), in letteratura sono stati proposti fattori di conversione (FC) del campo di variazione in deviazione standard, che considerano la numerosità (N) del campione:

 

 

 

Questa tabella dei fattori di conversione, in funzione del numero di dati del campione che ha permesso di valutare il campo di variazione, è fondata sul presupposto che la distribuzione dei dati sia normale. Anche essa fornisce una stima approssimata della deviazione standard, ma più precisa del rapporto generico 0,25 appena citato. Infatti, come è osservabile nella tabella precedente centrale, dove

- per  = 25 si ha FC = 0,254

- per  = 30 si ha FC = 0,245

 questo ultimo rapporto è accettabile per un campione di 25-30 dati.

E’ una dimensione campionaria che ricorre con frequenza nella ricerca ambientale e biologica. Ma per in campioni di poche unità e per campioni formati da alcune centinaia di osservazioni questo metodo approssimato determina stime che possono essere ritenute troppo grossolane.

 

In assenza di esperienze e di dati citati in letteratura, in varie situazioni le informazioni sulla varianza e sul valore della media devono essere ricavate da uno studio preliminare, chiamato studio pilota.

Le dimensioni (n₁) di questo primo campione con deviazione standard (s₁) sono sempre minime, non sufficienti per ottenere un test significativo o per ricavare una media campionaria, con precisione desiderata. E’ quindi necessario raccogliere altri dati, per formare un campione complessivo che abbia le dimensioni () richieste, ma senza perdere o trascurare i dati () già raccolti. Nel suo volume del 1977, W. G. Cochran (vedi Sampling Techniques, John Wiley, New York),

 propone

 dove, oltre alla consueta simbologia,

-   = numero finale del campione complessivo,

-   = numero di dati del primo campione,

-   = deviazione standard del primo campione.

Il valore di t è fornito dalla tabella dei valori critici. Ma per avere i suoi gdl si richiede la conoscenza di , che è appunto il valore che si vuole calcolare. Per una stima iniziale alla probabilità a = 0.05 in un test con ipotesi alternativa bilaterale o per la costruzione di un intervallo di confidenza della media, una approssimazione generalmente accettata è assumere t = 2.

 

ESEMPIO 2.   Con 7 dati, è stata misurata s = 8,5. Quanti dati è necessario raccogliere per una misura che con probabilità del 95% sia compreso tra ± 2,9 il valore reale?

 

Risposta. Con t = 2     n₁ = 7     s₁ = 8,5     d = 2,9

 si stima

 

 che complessivamente serve un campione  con  45 dati.

Pertanto agli   = 7 già raccolti nello studio pilota, occorre  aggiungerne altri 38.

 

Sempre per stimare le dimensioni del campione utile per ottenere  una stima precisa del valore medio, a volte si dispone solamente del coefficiente di variazione. Questa misura di variazione ha il grande vantaggio di essere caratteristico di ogni fenomeno, di essere indipendente dal valore della media e quindi di essere spesso sia rintracciabile in letteratura sia direttamente applicabile al test.

Ricordando che in dati campionari il coefficiente di variazione

 è

 e che alla probabilità del 95%

 l’errore relativo desiderato (r è espresso in percentuale o come intervallo di confidenza espresso in percentuale) è

 si ricava

Con t = 2 e il valore del CV,

 la formula abbreviata diventa

 

ESEMPIO 3.   Con un CV = 0,70 quanti dati è necessario raccogliere per ottenere una media che abbia un errore relativo ± 20%?

 

Risposta. Con CV = 0,70   e   r = 20

 si stima

 che approssimativamente servono  = 49 dati.

E’ un valore alto, ma tipico della ricerca ambientale, caratterizzata da valori di variabilità che sono alti.

 

Quasi sempre nella ricerca biologica di laboratorio e in quella industriale, CV è sensibilmente minore di 0,5. Normalmente è vicino a 0,2; spesso è ancora inferiore. Di conseguenza, il numero di dati necessari () è minore, anche se la precisione con la quale si vuole calcolare la media è maggiore.

 

ESEMPIO 4.    Con un CV = 0,20 quanti dati è necessario raccogliere per ottenere una media che abbia un errore relativo ± 10%?

 

Risposta. Con CV = 0,20   e   r = 10

 si stima

 

 che approssimativamente servono  = 16 dati.

 

Per il confronto di una media campionaria con una media attesa o il confronto tra due medie occorre introdurre anche l’errore b. Questi metodi sono sviluppati nel capitolo relativo al test t di Student.

Per il confronto simultaneo tra più medie, sono state presentate nei capitoli dedicati all’ANOVA.

 

L’altro parametro importante, che spesso occorre stimare da un campione di  dati, è la varianza. Un metodo di valutazione approssimata del numero  di dati da raccogliere per ottenere una stima della varianza con la precisione desiderata è stata proposto da A. E. Mace nel 1964 nel suo volume Sample-Size Determination (Reinhold, New York).

Prefissato un errore  espresso in proporzione, sempre in campioni abbastanza grandi (quindi il risultato deve essere  > 30) e con dati distribuiti in modo normale come in tutti questi metodi che ricorrono al valore di Z,

 si può calcolare

 

 ricordando che in una distribuzione bilaterale

- per a = 0.05 si ha Z = 1,96

- per a = 0.01 si ha Z = 2,58

A proposito dei valori da assumere per impostare l’esperimento, è utile ricordare che la varianza è un quadrato e quindi che l’errore relativo accettato spesso è molto più grande di quello ammesso per la stima di una media.

 

ESEMPIO 5.    Quanti dati servono per stimare una varianza con un limite di confidenza di ± 35% alla probabilità a = 0.05 che il valore reale non sia compreso nell’intervallo?

 

Risposta. Con r = 0,35  e Z = 1,96

 si stima

 

 

 che approssimativamente serve un campione di  = 61 dati.

 

Questi calcoli possono essere fatti anche per una variabile discreta e quindi per un conteggio, quale il numero di individui di una specie, allo scopo di

-  stimare una proporzione o percentuale con l’approssimazione desiderata,

-  il conteggio in una distribuzione poissoniana, con l’errore massimo accettato

-  il conteggio in una distribuzione binomiale negativa, con l’errore massimo accettato

 

Il caso della proporzione con l’uso della distribuzione normale è già stato illustrato nei capitoli precedenti. Per utilizzare la distribuzione poissoniana e la binomiale negativa, oltre ai testi indicati in questo paragrafo e applicabile a conteggi in laboratorio, è utile l’articolo di Ecologia di J. M. Elliot del 1977 Some methods for the statistical analysis of sample of benthic invertebrates, pubblicato su Freshwater Biological Station Association, Scientific Publication n. 25, pp. 1 – 142).