IL DISEGNO SPERIMENTALE:

CAMPIONAMENTO, PROGRAMMAZIONE DELL’ESPERIMENTO E POTENZA

 

 

 

23.11. L’ASSENZA DELL’EVIDENZA NON E’ L’EVIDENZA DELL’ASSENZA; SIGNIFICATIVITA’ STATISTICA E RILEVANZA DISCIPLINARE

 

 

Quando un test fornisce una probabilità  superiore alla  prefissata, non si può rifiutare l’ipotesi nulla. Nelle conclusioni di articoli di statistica applicata, a volte è scritto che è stato dimostrato che l’ipotesi nulla è vera. E’ un concetto errato, che viene ripetuto sotto forme differenti.

Ad esempio, per convenzione un valore di P maggiore del 5% (P > 0.05) è definito non significativo. Quando, in un confronto tra due medie, il test fornisce una probabilità P maggiore di quella prefissata, si afferma che l’esperimento è risultato negativo.

Soprattutto nella meta analisi, quella parte della statistica che ha sviluppato i metodi per riassumere correttamente i risultati di più pubblicazioni, può avvenire che i vari esperimenti analizzati siano stati effettuati tutti su campioni troppo piccoli, non adeguati al raggiungimento della significatività. Ma, quando questi risultati non significativi vengono sintetizzati nella espressione che il fattore analizzato non ha alcun effetto, si commette un errore di logica.

Nel confronto tra farmaco e placebo, può avvenire che la riduzione della malattia risulti statisticamente non significativa, come si è verificato più volte recentemente per HIV-1. Ma scrivere  The interventions we used were insufficient to reduce HIV-1 incidence… (vedi di A. Kamali e alii nell’articolo del 2033 Syndomic menagement of sexually-transmitted infections and behaviour change interventions on transmission of HIV-1 in rural Uganda: a community randomised trial su Lancet Vol. 361, pp.: 645-652) è una conclusione errata, poiché

-  induce a credere che tra i due trattamenti non esista una differenza,

-  mentre in realtà in quell’esperimento manca l’evidenza che esista una differenza.

Sono due concetti notevolmente diversi.

 

L’espressione utilizzata è errata, in quanto suscita l’impressione che il problema sia stato affrontato e che la risposta sia negativa in modo definitivo. L’amministratore è indotto a non intervenire, in quanto nel testo scientifico si afferma implicitamente che gli effetti della sua azione sarebbero nulli.

La conclusione reale è diversa: occorre raccogliere più osservazioni, per raggiungere l’evidenza statistica che la cura ha effetti positivi. Resta da valutare, al di fuori della statistica, se quel livello di miglioramento sia importante oppure trascurabile, sotto l’aspetto disciplinare.

 

Il problema dell’interpretazione errata, quando le differenze non hanno raggiunto la significatività statistica, è trattato in alcune pubblicazioni.

Recentemente, nella presentazione di questi argomenti è ripetuto il titolo esplicativo Absence of evidence is not evidence of absence, come negli articoli di

 

-  Phil Anderson del 2004 sulla rivista British Medical Journal (Vol. 328, pp. 476-477)

-  Douglas G. Altman e J. Martin Bland del 1995 su British Medical Journal (Vol. 311, pp. 485).

 

E’ comunque vero che un farmaco potrebbe non avere un effetto reale oppure non essere di fatto migliore del precedente. Si pone quindi il problema di rispondere alla domanda:

-  in un test statistico, quando è ragionevole dichiarare che un effetto è nullo oppure che non esiste una differenza tra due medie?

La risposta corretta è “mai”, poiché esiste sempre un certo livello di incertezza: The correct answer is “never”, because some uncertainty will always exist (Anderson, pag. 477).

 

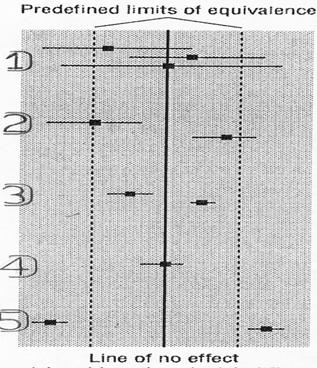
Tuttavia, è possibile fornire una risposta meno estrema, attraverso procedure logiche che sono fondate sull’importanza che la differenza analizzata statisticamente assume nella disciplina.

Nell’articolo citato, Phil Anderson riporta lo schema grafico sottostante, rielaborato da quello pubblicato nel testo di P. Armitage, G. Berry and J. N. S. Matthews del 2002 Statistical Methods in medical reseach (4^th ed. Oxford, Blackwell Science).

 

 

 

L’esempio, a carattere medico e di facile comprensione, valuta i possibili risultati del confronto tra gli effetti medi di due farmaci.

In un test, qui esemplificato per un intervallo di confidenza di due medie e della loro differenza, prima di interpretare i risultati sotto l’aspetto statistico sarebbe sempre importante

-  predefinire in modo esplicito i limiti di equivalenza, entro i quali l’effetto tra i due farmaci non è ritenuto clinicamente importante.

Più in generale e in qualsiasi disciplina, prima di ogni confronto statistico è necessario rispondere alla domanda: quali valori di differenza sono da ritenere importanti?

Ad esempio, è ovvio che se si confrontano farmaci per individui ipertesi, non ha senso una cura nuova che abbassi la pressione solamente di 2 o 3 punti rispetto alla precedente: anche se tale miglioramento  è reale, il suo effetto clinico è nullo o totalmente trascurabile. Diverso può essere il caso quando la diminuzione della pressione è di 20 o 30 punti. Ma la decisione del valore limite di accettabilità compete al medico, in funzione delle caratteristiche del paziente, degli effetti che induce e dei costi.

 

Nella figura precedente, i due limiti di equivalenza clinica tra due farmaci sono individuati dalle due rette punteggiate, poste a distanza uguale da una differenza media uguale a 0, evidenziata dal tratto continuo.

Rispetto a questi limiti clinici, l’analisi statistica può produrre 5 risultati, rappresentati con i numeri da 1) a 5) nella figura, che devono essere interpretati in modo corretto.

 

1)    Le medie dei due gruppi hanno intervalli di confidenza molto ampi, rispetto ai limiti di equivalenza clinica. La differenza tra le due medie (collocata al centro per costruzione) ha un intervallo grande (è la somma dei due precedenti), che supera i limiti di equivalenza predefiniti. La conclusione di questa analisi statistica è che si ha una

-  evidenza statistica insufficiente, per confermare o escludere che esita una differenza importante, tra i due farmaci.

Infatti,

-  se la differenza reale cade entro i limiti di equivalenza, la differenza esiste ma non è clinicamente importante;

-  mentre se la differenza reale cade fuori dai limiti di equivalenza, tra i due farmaci avremmo una differenza clinicamente importante.

Ma, con il test, non è stato individuato se la differenza vera sia entro o fuori i limiti di equivalenza medica.

 

2)    Le medie dei due gruppi hanno intervalli di confidenza di dimensioni medie e sono collocate vicino ai limiti di equivalenza. La media di un gruppo è lontana dell’intervallo di confidenza dell'altra, ma entrambe sono vicine ai limiti di equivalenza. La conclusione corretta è

-  la differenza tra le due medie è statisticamente significativa, ma non è certo che essa sia clinicamente importante.

 

3)    Le medie dei due gruppi hanno intervalli di confidenza piccoli, che sono collocati totalmente entro i limiti di equivalenza clinica. La conclusione corretta è

-  la differenza tra le due medie è statisticamente significativa, ma è clinicamente trascurabile o irrilevante.

 

4)    La differenza tra le medie dei due gruppi ha un intervallo di confidenza molto piccolo, collocato totalmente entro i limiti di equivalenza clinica. La conclusione corretta è

-  la differenza tra le due medie è statisticamente non significativa ed è clinicamente trascurabile o irrilevante.

 

5)   Le medie dei due gruppi hanno intervalli di confidenza piccoli, che sono collocati totalmente fuori dai limiti di equivalenza clinica. La conclusione corretta è

-  la differenza tra le due medie è statisticamente significativa ed è clinicamente importante.

Questa è la conclusione che si vorrebbe sempre raggiungere, quando si propone un farmaco nuovo.

Spesso è quella che le riviste chiedono, per pubblicare l’articolo inviato.

 

Quanto affermato per il confronto tra due medie è valido anche per il confronto tra due varianze.

Sei gruppi sono più di due, per applicare lo stesso modello logico è sufficiente riportate le due medie (o le due varianze) estreme

 

Per impostare un esperimento che possa raggiungere questo risultato, che di norma assicura la pubblicazione della scoperta e/o la commercializzazione del prodotto, è sempre vantaggioso impostare correttamente l’esperimento. In questo caso, significa

- avere utilizzato un campione abbastanza grande, quindi averlo scelto dopo aver stimato la dimensione minima ,

- sulla base della differenza , che rappresenta l’effetto minimo che può essere ritenuto clinicamente importante, ovviamente considerando gli altri 3 parametri ().

 

Per evitare gli errori descritti all’inizio del paragrafo, le raccomandazioni sono numerose. Una è l’abolizione  della terminologia che può indurre in errore, come propone I. Chalmers nell’articolo del 1985 Proposal to outlaw the term “negative trial” (su British Medical Journal, Vol. 290, p. 1002). Secondo Phil Anderson (pag. 477),  si dovrebbe favorire la cultura di una interpretazione corretta delle analisi statistiche. A questo scopo, sarebbe importante che le riviste pubblicassero anche i risultati incerti, dove la parte fondamentale delle conclusioni è la discussione del risultato: … journals need to be willing to publish uncertain results and thus reduce the pressure on researchers to reports their results as definitive. We need to create a culture that is comfortable with estimating and discussing uncertainly.

Affermazioni dello stesso tenore sono riportate anche nell’articolo dell’anno 2000 di P. Anderson e I. Roberts, dal titolo esplicativo e più drastico Should journals publish systematic reviews that find no evidence to guide pratice? Examples from injury research (su British Medical Journal, Vol. 320, pp. 376-377).