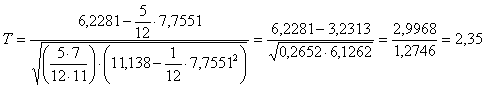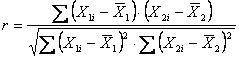ALTRI METODI INFERENZIALI:

NORMAL SCORES E RICAMPIONAMENTO

 

 

 

22.3.  APPLICAZIONE DEI NORMAL SCORES DI VAN DER WAERDEN A TEST PER OMOSCHEDASTICITA’, REGRESSIONE E CORRELAZIONE SEMPLICI

 

La trasformazione di van der Waerden può essere applicata anche in test che verificano ipotesi differenti da quelle sulla tendenza centrale. In letteratura, soprattutto nei testi internazionali di statistica nonparametrica, si t rovano esempi su

-  la omoschedasticità per due campioni,

-  la regressione e la correlazione semplici.

 

 

ESEMPIO 1 (OMOGENEITA’ DELLA VARIANZA PER DUE CAMPIONI CON TEST Z). Proposto da Jerome Klotz nel 1962 con l’articolo Nonparametric tests for scale (pubblicato su The Annals of Mathematical Statistics, vol. 33, pp. 498-512), in analogia agli altri test non parametrici è da utilizzare in alternativa al test parametrico F fondato sul rapporto tra le due varianze. Come noto, questo test parametrico perde in robustezza, quando la distribuzione dei dati si allontana dalla normalit. E’ quanto evidenzia appunto Klotz nel proporre il suo metodo: Because of the lack of robustness of the F-test with departures from normality… .

Tra i testi internazionali è riportato in W. J. Conover del 1999 Practical Nonparametric Statistics (3^rd ed. John Wiley & Sons, New York, VIII + 584 p.).

Fondato su gli stessi concetti del test di Levene, applica la metodologia dei normal scores agli scarti di ogni valore dalla sua media. Ad esempio, si supponga di voler valutare se esiste una differenza significativa nella variabilità tra il prodotto di due industrie differenti. A questo scopo sono stati analizzati 5 campioni dell’azienda A e 7 campioni dell’azienda B.

 

Per testare l’ipotesi nulla

H₀:

 contro un’ipotesi che può essere unilaterale oppure bilaterale, la metodologia prevede i seguenti passaggi:

 

1 – Per ognuna delle due serie (A e B) di dati calcolare la media () e gli scarti da essa () con il loro segno

 

 

 

2 – Ordinare gli scarti dal minore al maggiore, considerando il segno e mantenendo l’informazione di gruppo (colonne 1, 2 della tabella successiva); già questa semplice elaborazione evidenzia come, con i dati dell’esempio, gli scarti del gruppo A abbiano una variabilità maggiore, occupando contemporaneamente sia i ranghi minori sia quelli maggiori;

ma si tratta di valutarne la significatività con un test

 

 

 

3 – Dopo aver riportato i ranghi  (colonna 3) e calcolato i quantili  (colonna 4)

 attraverso la relazione

 

4 – si trasformano i quantili  (colonna 4) nei normal scores  (colonna 5)

 

5 – I valori dei normal scores  sono elevati al quadrato (in colonna 6), tenendo separati quelli del gruppo minore (di  in colonna 7); infine sono elevati alla quarta ( in colonna 8)

 

6 -  Dopo aver definito

-  = numero di dati del gruppo minore; nell’esempio  = 5

-  = numero di dati del gruppo minore; nell’esempio  = 7

-  = numero totale di dati ( =  + ); nell’esempio  = 12

 si calcolano le somme

- ; con i dati dell’esempio  = 7,7551

- ; con i dati dell’esempio  = 6,2281

- ; con i dati dell’esempio  = 11,138

(La scelta di sommare i dati del gruppo minore ha una motivazione solamente pratica, come in tutti i casi in cui si ricorre alla somma di uno solo dei due gruppi).

 

7 – Infine si calcola

 

Con i dati dell’esempio

 

si ottiene T = 2,35.

 

8 – Il valore di  ha una distribuzione asintoticamente normale. Nella tabella della distribuzione normale ridotta Z, bilaterale in base alla domanda espressa in questo esempio, a Z = 2,35 corrisponde la probabilità P = 0,019. Si rifiuta l’ipotesi nulla.

Se la domanda fosse stata unilaterale, come quando si vuole verificare se una delle due varianze è significativamente maggiore oppure minore sulla base di informazioni esterne al campione raccolto, la probabilità sarebbe stata P = 0,09.

 

 

ESEMPIO 2 (CALCOLO DEL COEFFICIENTE DI CORRELAZIONE). Sviluppando le brevi indicazioni riportate nel testo di W. J. Conover del 1999, Practical Nonparametric Statistics (3^rd ed. John Wiley & Sons, New York, VIII + 584 p.), il metodo dei normal scores è utile anche per calcolare il coefficiente di correlazione semplice. Indicato con r (rho) è analogo al coefficiente di correlazione prodotto momento di Pearson (Pearson product moment correlation coefficient). Ad esempio, riprendendo la serie di misure utilizzate per le misure di correlazione non parametrica r di Spearman e t di Kendall

 

 

 

 il metodo richiede una serie di passaggi logici

 

 

 

 

1 – Come riportato nella tabella, i valori rilevati di X e Y (riportati in colonna 1 – Dati) dapprima sono trasformati nei loro ranghi (colonna 2 – R_i) e infine

mediante la relazione

 nelle proporzioni (colonna 3 – P_i)

 

2 – Ricorrendo alla tabella, si trasformano i valori P_i in valori Z_i con il loro segno (colonna 4 – Z_i)

- sia per la colonna dei valori X_i che diventano A_i,

- sia per la colonna dei valori Y_i che diventano B_i,

 

3 – La correlazione parametrica, il cui coefficiente  con le variabili X₁ e X₂

è ricavato da

 

 nel caso di ranghi trasformati in valori Z, che sono uguali per le due variabili, con formula abbreviata

 diventa

  

 

Con i dati dell’esempio, si ottiene

 una correlazione positiva r = +0,85.

 

4 - La sua significatività è testata con la solita metodologia richiesta dal coefficiente di correlazione  r di Spearman, al quale si rinvia.

 

5 - Il metodo richiede che non esistano ties o siano presenti solo in numero limitato.