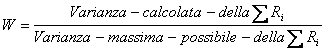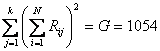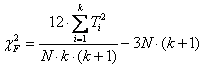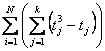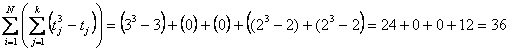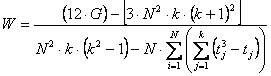TEST NON PARAMETRICI

PER CORRELAZIONE, CONCORDANZA,

REGRESSIONE MONOTONICA E REGRESSIONE LINEARE

 

 

21.8.  IL COEFFICIENTE DI CONCORDANZA TRA VALUTATORI: LA W DI KENDALL. SUE RELAZIONI CON LA CORRELAZIONE NON PARAMETRICA E CON IL TEST DI FRIEDMAN PER K CAMPIONI DIPENDENTI. CENNI SULLA TOP-DOWN CONCORDANCE

 

 

I coefficienti di correlazione  di Spearman e  di Kendall sono applicato a due variabili, cioè a due serie di ranghi (o di valori trasformati in ranghi), relativi a N oggetti o individui. Con gli indici di concordanza, è possibile verificare l’accordo complessivo tra più variabili quando

-  si dispone di k serie di ranghi,

-  riportati per N valutazioni.

 

I test proposti per queste misure di associazione - correlazione, definite con il termine tecnico di concordanza, sono numerosi. Alcuni sono pubblicati nel volume di Sir Maurice George Kendall (1907-1983) divulgato nel 1970 (Ranks correlation methods, 4^th ed. stampato a Londra da Griffin) e nella sua edizione più recente, sempre di Sir  M. G. Kendall ma con J. D. Gibbons del 1980 (Ranks Correlation Methods, 5^th ed. stampato a Londra da Edward Arnold).

Tra le misure di concordanza che è possibile trovare nella letteratura statistica, quella più frequentemente proposta nei programmi informatici e nei testi internazionali a maggior diffusione è il coefficiente di concordanza W di Kendall (Kendall’s Coefficient of Concordance).

 

La metodologia è stata proposta in modo indipendente con due articoli pubblicati quasi contemporaneamente nel 1939:

-  il primo da M. G. Kendall e B. Babington-Smith (vedi The problem of m rankings, su The Annals of Mathematical Statistics Vol. 10, pp. 275-287), 

-  il secondo da W. A. Wallis (vedi The correlation ratio for ranked data, su Journal of the American Statistical Association, Vol. 34, pp. 533-538).

 

Le misure di associazione e di concordanza non sono test inferenziali: hanno solamente un valore descrittivo della intensità della relazione. E’ quindi sempre importante verificare la significatività del valore calcolato mediante test inferenziali.

Il coefficiente di concordanza W è costruito in modo tale da assumere solamente valori che variano tra 0 e +1:

Quando

-   esiste totale accordo tra le N serie di k ranghi, si ha W = 1

-   le N serie di k ranghi sono puramente casuali, si ha W = 0.

Il valore di W non può essere negativo, in quanto con N serie di k ranghi non è possibile avere tra esse disaccordo completo.

 

Il coefficiente di concordanza W di Kendall può essere visto con due ottiche diverse:

-   una generalizzazione del test  e del test t: infatti esso misura la divergenza nella valutazione tra N serie di k misure ordinali,

-  una analisi della varianza non parametrica a due criteri di classificazione; infatti può essere utilizzato nelle stesse condizioni del test di Friedman, in quanto entrambi sono fondati sullo stesso modello matematico: pertanto la significatività può essere determinata nello stesso modo mediante il c² o il test F.

 

Queste due relazioni, in particolare quella con il test di Friedman, sono presentati in modo più approfondito nella seconda parte del paragrafo.

 

L’indice di divergenza W può essere calcolato direttamente da una serie di dati.

 

Si supponga che 4 ricercatori (I, II, II, IV) debbano stabilire una classifica tra 5 situazioni ambientali (a, b, c, d, e), per valutare il loro livello di degrado:

 

 

 

Successivamente o al momento della graduatoria, i punteggi attribuiti dagli N ricercatori alle k situazioni ambientali (A, B, C, D, E) sono trasformati in ranghi entro la stessa riga, attribuendo 1 al valore minore ed k a quello maggiore.

Per esempio,

-  secondo il ricercatore I la situazione B è quella meno degradata e la D quella maggiormente degradata,

-  mentre il ricercatore II  valuta la situazione A come migliore e la C come quella peggiore.

 

Se fosse vera l’ipotesi nulla H₀ dell’assenza totale d’accordo tra i ricercatori (cioè essi hanno fornito valutazioni di rango sulla base di principi totalmente differenti), le somme dei ranghi per colonna () sarebbero tra loro uguali e le medie per colonna () uguali alla media generale.

 

Viceversa, se fosse vera l’ipotesi alternativa H₁ di pieno accordo tra i ricercatori (essi forniscono la stessa valutazione sulle k situazioni), le somme () e le medie relative () avrebbero differenze massime.

 

Se l’ipotesi nulla (H₀) fosse vera, l’indice di divergenza dovrebbe essere W = 0.

Nel caso opposto (H₀ falsa) di massima divergenza, l’indice dovrebbe essere W = 1.

 

L’ottimo testo di statistica applicata di David H. Sheskin pubblicato nel 2000 (Handbook of PARAMETRIC and NONPARAMETRIC STATISTICAL PROCEDURES, 2^nd ed. Chapman & Hall/CRC, London, 982 p.) presenta in modo dettagliato la procedura, qui ulteriormente chiarita in tutti i suoi passaggi logici e metodologici.

 

Si supponga, come nella tabella successiva, che sei esperti (indicati da I a VI; quindi N = 6) abbiano espresso un giudizio su 4 prodotti o situazioni (indicati con A, B, C, D; quindi k = 4). La loro valutazione, espressa direttamente in ranghi o per trasformazione successiva, è stata

 

 

 

 

Vi vuole verificare se i sei esperti concordano globalmente nella loro valutazione, in modo significativo.

 

Risposta. In termini più tecnici,

-  dopo aver fornito una misura della concordanza (W) degli N valutatori, dove

 

 

-  si intende verificare la sua significatività, cioè testare l’ipotesi

H₀: W = 0       contro      H₁: W ¹ 0

 

Con metodi del tutto analoghi a quelli della varianza tra trattamenti, di cui è riportata la formula abbreviata,

- dapprima si calcolano i totali

 

 

-  successivamente si ricava il coefficiente di concordanza W con

 

 

 

 ottenendo

 

Con formula ulteriormente semplificata che, come molte di esse, ha il difetto di nascondere i concetti, è possibile il calcolo più rapido

 

 

Nel caso di piccoli campioni (k da 3 a 7; N da 3 a 20), sono stabiliti valori critici ricavati da quelli proposti da M. Friedman nel 1940 per il suo test (in A comparison of alternative tests of significance for the problem of m rankings, pubblicato su Annals of Mathematical Statistics, Vol. 11, pp. 86-92).

Nel caso dell’esempio, con N = 6 e k = 4 il valore critico alla probabilità a = 0.01 è 0,553. Poiché il valore calcolato è superiore a quello critico, si rifiuta l’ipotesi nulla con probabilità P inferiore a 0.01. Esiste un accordo molto significativo tra i 6 esperti nell’attribuzione della graduatoria ai 4 prodotti.

 

Per grandi campioni, ma con limiti non chiaramente definibili come in tutti questi casi, una buona approssimazione è data dalla distribuzione c² con gdl = k - 1 dopo la trasformazione di W

 mediante la relazione

 

Valori critici del Coefficiente di Concordanza W di Kendall

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Con i dati dell’esempio,

 si ottiene un valore del chi quadrato uguale a 15,40 con 3 gdl.

Poiché nella tabella dei valori critici con a = 0.01 il valore riportato è 11,34 si rifiuta l’ipotesi nulla con probabilità di errare P < 0.01.

 

La corrispondenza di questo test con il test di Friedman offre altre soluzioni per valutare la significatività del valore W calcolato.

 

Caso di piccoli campioni.

Applicato ai dati dell’esempio, il test di Friedman serve per decidere se i totali dei ranghi (T_i  osservati), sommati per colonna, sono significativamente differenti dell’atteso.

Per il test, si calcola la statistica Fr

Fr = 

E’ ovvio che tale valore di Fr tenderà

-  a 0 nel caso di accordo tra totali osservati e totali attesi (H₀ vera e casualità della distribuzione dei ranghi),

-  a un valore alto al crescere dello scarto tra essi (H₀ falsa e attribuzione sistematicamente differente dei ranghi ai fattori riportati in colonna)

 

Con i dati dell’esempio ( = 20, 11, 7, 22), poiché N = 6 e k = 4  la somma attesa dei ranghi per colonna è

6 x (4+1)/2 = 15

 ovviamente corrisponde alla somma totale dei ranghi (60) diviso k (4).

 

Con la formula presentata, si ottiene

Fr = (20 – 15)² + (11 – 15)² + (7 – 15)² + (22 – 15)² = 5² + 4² + 8² + 7² =  25 + 16 + 64 + 49 = 154

 un valore di Fr uguale a 154.

 

Poiché nella tabella di Friedman per piccoli campioni i valori critici Fr riportati sono

-  Fr = 102 alla probabilità a = 0.01

-  Fr =128 alla probabilità a = 0.001

 è possibile rifiutare l’ipotesi nulla H₀: W = 0 e accettare implicitamente  H₁: W ¹ 0 con probabilità P < 0.001.

Nel caso di grandi campioni, come già presentato nel paragrafo dedicato al test di Friedman,

 si può calcolare il chi quadrato relativo

 

 c²_F   =    

 in cui

-  la seconda parte è data dagli scarti al quadrato tra somma osservata ed attesa,

-  mentre la prima dipende dall’errore standard, determinato numero di dati, trattandosi di ranghi.

 

La formula abbreviata che ricorre con frequenza maggiore nei testi di statistica è

 

 dove:

-  N  è il numero di righe od osservazioni in ogni campione (tutte con il medesimo numero di dati),

-  k  è il numero di colonne o campioni a confronto,

-  T_i   è la somma dei ranghi della colonna  e la sommatoria  è estesa a tutte le colonne.

 

Sempre con i dati dell’esempio ( = 20, 11, 7, 22), poiché N = 6 e k = 4

 

 

 si ottiene  = 15,4

E’ un risultato che fornisce una probabilità a del tutto coincidente con quello ottenuto mediante la W (W = 0,8556).

 

Infatti è possibile passare dall’uno all’altro, sulla base delle due relazioni:

-  da W a  

 = 6 × (4 - 1) × 0,8556 = 15,4

-  da  a W

 =  = 0,8556

 

La corrispondenza tra coefficiente di concordanza W di Kendall e coefficiente di correlazione per ranghi di Spearman è importante per i concetti implicati; meno dal punto di vista pratico. Per tale motivo si rinvia a testi che lo presentano in modo dettagliato. Tra essi, quello David H. Sheskin pubblicato nel 2000 (Handbook of PARAMETRIC and NONPARAMETRIC STATISTICAL PROCEDURES, 2^nd ed. Chapman & Hall/CRC, London, 982 p.). Il concetto di base, che è possibile dimostrare in modo semplice con un esempio, è che con N valutatori, mediante il r di Spearman è possibile calcolare tutte le correlazioni semplici tra loro, pari alle combinazioni 2 a 2  dei k oggetti.  La media () di tutti questi coefficienti di correlazione r è in relazione diretta con il valore di W, mediante il rapporto

 = 

 

TIES

Come tutte le misure fondate sui ranghi, anche nel caso della W di Kendall  si richiede che la scala utilizzata per attribuire i punteggi sia continua, in modo tale da non avere valori identici. Non sempre è possibile, poiché in realtà la scala che spesso viene usata è di fatto limitata e quindi si determinano ties.

Quando i ties sono pochi, è possibile apportare una correzione, il cui effetto è sempre quella di aumentare il valore di W, poiché ne riduce la varianza.

 

Il seguente esempio dove N = 4 e k = 4

 

 

 

 

 utilizza un campione molto piccolo, che ha finalità esclusivamente didattiche anche se è riportato nelle tabelle dei valori critici come caso possibile nella ricerca applicata. In esso si osserva che

-  nella prima riga é presente un ties con 3 valori identici,

-  nella quarta riga sono presenti due ties, ognuno con 2 valori identici.

Per la correzione si deve stimare

 dove con i dati dell’esempio si ha

-   per la riga 1 t_j = 3,

-   per la riga 2 t_j = 0,

-   per la riga 3 t_j = 0,

-   per la riga 4 t_j = 2, due volte

 

Applicando la formula indicata, si ottiene

 

 

 e il coefficiente di concordanza W che, senza correzione, sarebbe stato

 

 

 W = 0,4375

 

 mentre con la correzione diviene

 

 

 

 W = 0,5147.

 

Poiché per N = 4  e  k = 4  alla probabilità a = 0.05 il valore critico è 0,619 con W = 0,5147 non è possibile rifiutare l’ipotesi nulla.

E’ tuttavia evidente l’effetto della correzione per i ties, (aumento del valore W di concordanza da 0,4375 a 0,5147) tanto più marcato quanto più ampio è il ties.

 

Il coefficiente di concordanza W di Kendall valuta l’intensità di gradimento come nei casi illustrati; ma è utilizzato anche per misurare la concordanza complessiva fra tre o più variabili. E’ infatti chiamato anche Rank Correlation among Several Variables. Con le modalità qui illustrate, è applicato spesso ai casi descritti nel paragrafo dedicato alla correlazione parziale.

Il testo di Jarrold H. Zar del 1999 (Biostatistical Analysis, 4^th ed. Prentice – Hall, Inc. Ney Jersey, 663 p + App. 212) sviluppa in particolare esempi di questo tipo. Per approfondimenti sull’argomento si rimanda ad esso.

 

Nello stesso testo è spiegata anche la Top-Down Concordance, chiamata anche Weighted rank/top-down concordance. Con essa, si prendono in considerazione le situazioni caratterizzate dai punteggi estremi. Nell’esempio delle valutazioni forniti da 6 esperti su 4 prodotti, serve per verificare se coloro che concordano nel dare la loro preferenza (rango 1) al prodotto C sono concordi anche nell’attribuire il punteggio minimo (rango 4) al prodotto D o viceversa.

Nella ricerca ambientale e industriale, dove si svolgono indagini sulle opinioni o sui consumi, può essere utilizzato per valutare se il gradimento massimo dato a una situazione è strettamente correlato con il livello di gradimento minimo espresso per un’altra situazione o prodotto

Nell’assunzione di personale, in cui 4 dirigenti (N = 4) danno una valutazione in ranghi di k canditati, oltre a valutare se essi concordano globalmente nel giudizio con il test illustrato nella prima parte del paragrafo, è possibile valutare se quando concordano all’attribuire il punteggio più alto a un candidato concordano pure nell’attribuzione del punteggio minore. Nell’esempio riportato da Zar, dove 3 ragazzi esprimono il loro gradimento a 6 differenti gusti di gelato, si vuole valutare se coloro che preferiscono un certo gusto concordano anche nella bassa preferenza da essi attribuita a un altro sapore.

Anche in questo caso si rinvia a questo testo per approfondimenti.