TEST NON PARAMETRICI

PER CORRELAZIONE, CONCORDANZA,

REGRESSIONE MONOTONICA E REGRESSIONE LINEARE

 

 

 

21.14.  LA REGRESSIONE LINEARE NON PARAMETRICA CON IL METODO DEI TRE GRUPPI DI BARTLETT

 

 

Oltre al metodo di Theil, la cui significatività è analizzata mediante la correlazione non parametrica t di Kendall e pertanto il metodo è chiamato sia Theil-Kendall, sia metodo robusto di Kendall (Kendall’s robust line-fit method), un altro metodo non parametrico ancora più semplice e rapido, ma molto meno diffuso, è riportato nei testi di

- Robert R. Sokal  e F. James Rohlf del 1995 Biometry. The principles and practice of statistics in biological research (3^rd ed. W. H. Freeman and Company, New York,  XIX, + 887 p.).

- Owen L. Davis e Peter L. Goldsmith del 1980 Statistical Methods in Research and Production, with special reference to Chemical Industry (4^th  Revised Edition, published for Imperial Chemical Industries Limited, Longman Group Limited, London , XIII + 478 pp.)

 

E’ il metodo di Bartlett o più estesamente

-   metodo dei tre gruppi di Bartlett (Bartlett’s three-group method),

 proposto appunto da M. S. Bartlett nel 1949 con l'articolo Fitting a Straight Line when Both variables are Subject to Error (pubblicato su Biometrics Vol. 5 , pp.: 207-212).

La procedura del test può essere illustrata sviluppando un esempio già utilizzato per presentare il metodo di Theil, sia per mostrarne con maggiore evidenza i differenti approcci sia per favorire il confronto tra i risultati.

 

Si supponga di voler valutare la crescita media di una specie animale con l’aumentare dell’età, in una fase della vita in cui la successione dei valori nel tempo può essere considerata lineare. Ma, in questo esempio, per l’analisi si dispone solamente dei valori medi di un gruppo individui.

Ne consegue che non è possibile ricorrere alla statistica parametrica, poiché nei test d’inferenza parametrici si richiede sempre la variabilità d’errore sia valutata a partire dalle singole osservazioni.

 

Per il problema presentato, sono stati raccolti campioni di individui con età variabile da 4 a 20 giorni (X) e stimando per ogni età la dimensione media del campione (Y):

 

 

Età  X	4	5	6	7	8	9	10	11	12
Lungh. Y	40	45	51	55	60	67	68	65	71

 

 

 

La procedura richiede la seguente serie di passaggi logici:

 

 1 - Ordinare i valori della variabile X, in modo crescente. In questo caso, essendo X il tempo o l'età, la variabile X è già ordinata.

 

 2 - Prendendo i valori secondo l'ordine della X, costruire tre gruppi di dimensioni possibilmente uguali, in particolare devono avere lo stesso numero di osservazioni il primo e il terzo gruppo.

Con i dati dell'esempio ( = 17), appare logico formare i tre gruppi con un numero di dati uguale a 6, 5 e 6 rispettivamente

 

 

 

 

 3 – Da questi dati occorre calcolare le medie del gruppo 1 e del gruppo 3

-    = 6,50      = 53,00

-    = 17,50      = 82,17

 e le due medie generali considerando tutti i 17 dati

 

    

 

 4 – Il coefficiente angolare  è

 

 

 5 – L’intercetta  è

 

 

 6 – Infine la retta non parametrica di Bartlett è

 

 

 7 – La retta non parametrica con il metodo abbreviato di Theil, presentata nei paragrafi precedenti, risultava

 

Tra i due metodi,

-  la preferenza degli statistici è attribuita al metodo di Theil,

 in quanto utilizza le mediane. Ne deriva che è meno sensibile alla eventuale non normalità della distribuzione, in particolare alla asimmetria determinata dalla presenza di dati anomali: la dizione di metodo robusto attribuito da vari statistici  al metodo di Theil – Kendall (Kendall’s robust line-fit method) dipende appunto da queste osservazioni.

 

Per la significatività della regressione lineare, anche con questo metodo di Bartlett

-  si può ricorrere alla correlazione non parametrica (il t di Kendall oppure il r di Spearman, indifferentemente).

Se il test di correlazione risulta significativo, si può affermare che è significativa anche la retta non parametrica. Vale a dire che

-  la serie dei dati trasformati in ranghi cresce in modo lineare

-  e quindi la serie dei valori reali cresce in modo monotonico (concetto già illustrato nei paragrafi precedenti)

 

Una applicazione di questo test è richiesta nel caso della Regressione Modello II, anche se forse risulta ancora più appropriato il metodo di Theil - Kendall.

L’esempio successivo utilizza dati che richiedono appunto una analisi Model II Regression, discussa in un capitolo precedente.

 

ESEMPIO (TRATTO DA Sokal e Rohlf pag. 547-549).  Si supponga di voler valutare la relazione lineare tra il peso di alcune femmine di un pesce della California Scorpaenichthys marmoratus (espresso in 100 g) e il numero di uova prodotto (in migliaia), con un campione di 11 misure, nel quale entrambe le variabili sono soggette ai medesimi errori di rilevazione o determinazione delle dimensioni:

 

 

Calcolare la retta con il metodo dei tre gruppi di Bartlett.

 

Risposta. Dai dati della tabella è bene ricavare la organizzazione in gruppi, dopo aver ordinato i dati in modo crescente per la variabile X (in questo caso, nel testo sono già ordinate)

 

 1 - Si ricava la tabella

 

 

 

 2 -  e da essa le medie del gruppo 1 e del gruppo 3

-           

-       

 

e le due medie generali considerando tutti gli 11 dati

 

    

 

 3 – Il coefficiente angolare  è

 

 

 4 – L’intercetta  è

 

 

 5 – Infine la retta non parametrica di Bartlett è

 

Se su questi dati fosse stata calcolata la retta di regressione lineare parametrica (da verificare come esercizio), secondo il testo si sarebbe trovata

 

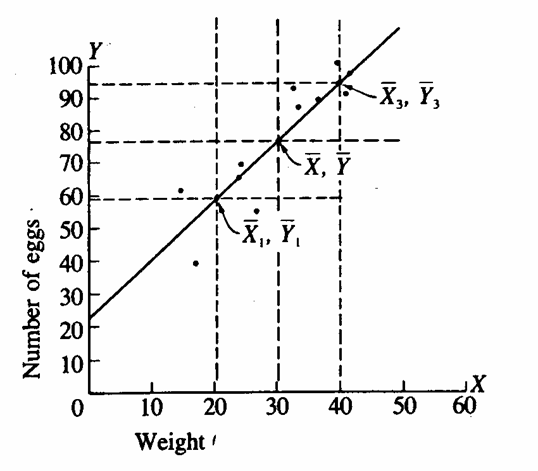
In tutti i casi di analisi della regressione lineare e della correlazione, è sempre utile riportare il grafico o diagramma di dispersione, con la retta relativa

 

 

In essa si evidenziano le caratteristiche della distribuzione dei dati, in particolare la presenza di eventuali valori anomali, mostra se i punti sono distribuiti

-   in modo casuale e approssimativamente  bilanciato (situazione corretta)

-  oppure in modo regolare o con la maggioranza dei punti da una sola parte della retta (situazione errata).

 

Inoltre è possibile osservare come la retta

- attraversi il baricentro complessivo dei dati

 di coordinate

   e   

 in quanto su di esse è stata calcolata l’intercetta  = 21,9

 

-  e si avvicini molto ai punti individuati dalle medie del gruppo 1 e del gruppo 3

 di coordinate

     e    

     e    

 in quanto con esse è stato ricavato il coefficiente angolare  = 1,8.

Se è presente un dato fortemente anomalo, tale da alterare sensibilmente una delle tre medie, la retta non attraversa i punti individuati dalle medie dei gruppi 1 e 3.