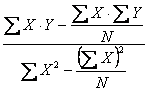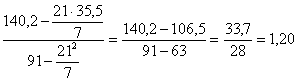TEST NON PARAMETRICI

PER CORRELAZIONE, CONCORDANZA,

REGRESSIONE MONOTONICA E REGRESSIONE LINEARE

 

 

21.12.   CONFRONTO TRA LA RETTA PARAMETRICA E LA RETTA DI THEIL

 

 

Ai fini di un’interpretazione corretta dei risultati della regressione, è sempre utile costruire il diagramma di dispersione dei punti campionari, con la retta relativa. Per una scelta ragionata, è necessario comprendere esattamente

-  sia le caratteristiche distintive della retta di regressione lineare semplice non parametrica, calcolata con il metodo di Theil,

-  sia le differenze rispetto a quella parametrica, calcolata con il principio dei minimi quadrati.

A questo scopo, dopo aver ripreso i dati dell’esempio precedente

 

 

 

 

- sui quali è stata calcolata la regressione di Theil nella versione estesa:

 

- si calcola anche la retta di regressione parametrica, che con i parametri stimati dai dati della tabella,

= 140,2      = 21      = 35,5      = 91      n = 7      = 3      = 5,07

 applicati alla formula per il coefficiente angolare

 

b =

 

si ottiene un valore di b

 

b =

 

 uguale a 1,20 e da esso un valore di a

a =

a = 1,47

 uguale a 1,47

 per cui la retta parametrica è

 

Sia il confronto visivo

-  tra i punti sperimentali e le due rette (figura successiva),

-  sia la differenza tra i valori di Y osservati (riga 1 nella tabella successiva)

-  e quelli calcolati con la retta di Theil (riga 2 nella tabella successiva)

-  e quella dei minimi quadrati (riga 3 nella tabella successiva)

 

 

 

 evidenzia come l’ultima osservazione sia anomala, rispetto alle altre 5; inoltre come la retta non parametrica si avvicini molto ai primi 5 punti ignorando praticamente l’ultimo dato, mentre la retta parametrica sia da esso attratta, allontanandosi dagli altri.

 

E’ una stima simile a quello della mediana rispetto alla media, in presenza di un valore anomalo. In questo caso, l’effetto di distorsione della stima parametrica rispetto ai dati reali è accentuato dal fatto che la retta parametrica minimizza la somma dei quadrati degli scarti.

Oltre che dalle condizioni di validità, la scelta dipende quindi dal valore che si vuole attribuire all’osservazione anomala, rispetto a tutte le altre.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

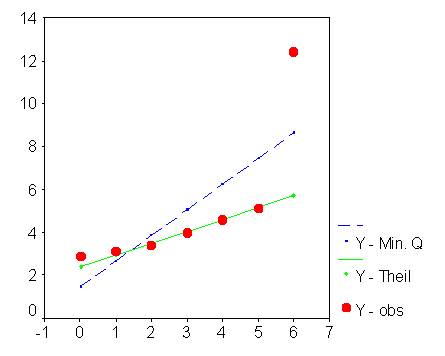Nel grafico,

- i punti sono i  7 valori osservati,

- la retta che incrocia i 6 punti e si avvicina al valore anomalo è la retta parametrica calcolata con il metodo dei minimi quadrati,

- la retta che passa per i 6 punti ed ignora il valore anomalo è quella non parametrica, calcolata con il metodo di Theil.