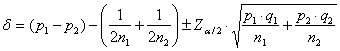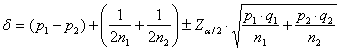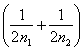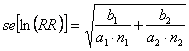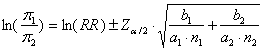|
COEFFICIENTI DI ASSOCIAZIONE, DI COGRADUAZIONE E DELL’ACCORDO RISCHIO RELATIVO E ODDS RATIO
20.10. DIFFERENZA TRA RISCHI E RISCHIO RELATIVO, CON INTERVALLI DI CONFIDENZA
Il test chi quadrato e il metodo esatto di Fisher per piccoli campioni in tabelle 2 x 2 servono per confrontare le frequenze tra due campioni indipendenti. L’ipotesi nulla H0 è che, nei due differenti gruppi (1 e 2), le frequenze relative di individui che hanno la caratteristica in esame siano uguali; in termini più tecnici, che siano due campioni estratti dalla medesima popolazione oppure da due popolazioni con la stessa frequenza relativa p. In simboli: H0: p1= p2
In varie situazioni, sempre con dati categoriali, per verificare l’effetto di una situazione alterata o disturbata rispetto a quella ritenuta normale, il confronto viene fatto con una situazione di controllo. In Medicina e Epidemiologia, spesso il confronto è tra persone esposte al rischio e persone non esposte. Indicando - con a1 il numero di persone con la malattia in un campione di persone esposte al rischio, di dimensioni n1, - con a2 il numero di persone con la malattia in un campione di persone non esposte al rischio, di dimensioni n2, si ottengono le due proporzioni o frequenze relative p1 e p2 con
In questa condizione sperimentale, può essere utile confrontare la proporzione di ammalati presente nelle persone esposte al rischio (p1) con quella presente nella situazione di controllo (p2). Le misure utili sono: la differenza tra rischi e il rapporto tra rischi o rischio relativo.
La differenza tra rischi (risk difference indicata con RD) è definita come RD = p1 – p2 Di essa è possibile calcolare l’intervallo di confidenza. La risk difference reale (d = p1 - p2), nel caso di grandi campioni e quindi solamente (come illustrato nel capitolo sul c2) quando si abbia - sia - sia con p1 - p2 positivo è
mentre con p1 - p2 negativo è
dove - - q = 1 - p. In entrambi i casi, la differenza RD = p1 - p2 è ridotta, in valore assoluto, della quantità
ESEMPIO 1. Su un campione di 4 mila persone che giornalmente assumono il farmaco X, 11 presentano i sintomi della malattia A. Nel campione di controllo, formato da 10 mila persone, gli individui affetti sono 7. Quale è la differenza tra rischi? Quale il suo intervallo di confidenza al 95% di probabilità?
Risposta. Dopo aver calcolato - p1 = 11/4000 = 0,00275 - p2 = 7/10000 = 0,00070 si stima la differenza tra rischi RD = 0,00275 - 0,0007 = 0,00205 che risulta RD = 0,00205. Per stimare il suo intervallo di confidenza, dapprima occorre verificare che siano realizzate entrambe le condizioni di validità relative alle dimensioni dei campioni. Nel caso dell’esempio - - in entrambi i campioni si hanno quantità superiori a 5. Si può utilizzare la distribuzione normale.
Con i dati dell’esempio - a = 0.05 in una distribuzione bilaterale il valore è Z = 1,96 - n1 = 4000 p1 = 0,00275 q1 = 0,99725 - n2 = 10000 p2 = 0,00070 q2 = 0,9993 si ricava che
la differenza reale tra le due proporzioni è d = 18,75 ± 17 per 10 mila. Espressa come proporzione, con una probabilità del 95 per cento la differenza reale tra le due popolazioni è compresa tra 0,000175 e 0,003575.
Più spesso si utilizza il rapporto tra rischi (risk ratio) o rischio relativo (relative risk indicato con RR), chiamato anche in modo più rapido rapporto R, definito come RR = p1/p2 La sua distribuzione è di tipo binomiale.
Per stimare l’intervallo di confidenza con la distribuzione Z, si deve assumere che RR sia distribuito in modo approssimativamente normale. Trattandosi di un rapporto, quindi con forte asimmetria destra, si deve ricorrere alla trasformazione logaritmica; in questo caso al log naturale
di cui è possibile calcolare la varianza, come pure per le due proporzioni p1 e p2, cioè ln(p1) e ln(p2). Per ln(p1) e ln(p2), con formula euristica, le varianze sono:
Poiché si ha che
con formula abbreviata le due varianze diventano
La varianza del ln del rapporto p1/p2, cioè di ln(RR) è la somma delle due varianze, cioè
L’indice calcolato RR è un valore medio. Quindi la radice quadrata della sua varianza, la deviazione standard, in realtà è un errore standard (se = standard error)
L’intervallo di confidenza del rischio relativo p1/p2, sempre nella condizione che il campione sia grande, quindi che - sia - sia alla probabilità a prestabilita, utilizzando il logaritmo è
Per l’uso dei logaritmi sono chiamati anche limiti logit. Dopo aver stimato il limite inferiore (l1) e il limite superiore (l2), si ritorna alla scala originale con
ESEMPIO 2. (con gli stessi dati dell’esempio 1). Su un campione di 4 mila persone che giornalmente assumono il farmaco X, 11 presentano i sintomi della malattia A. Nel campione di controllo, formato da 10 mila persone, gli individui affetti sono 7. Quale è il rischio relativo? Quale il suo intervallo di confidenza al 95% di probabilità?
Risposta. Dopo aver calcolato - p1 = 11/4000 = 0,00275 - p2 = 7/10000 = 0,00070 si stima il rischio relativo RR = che risulta RR = 3,929. Poiché le condizioni di validità sulle dimensioni del campione sono rispettate, come mostrato per questi dati nell’esempio 1, si può stimare l’intervallo di confidenza. Con - Z = 1,96 per una probabilità a = 0.05 in una distribuzione bilaterale - n1 = 4000 a1 = 11 b1 = 3989 - n2 = 10000 a2 = 7 b2 = 9993 si ricava che
- il limite inferiore è l1 = 1,638 – 0,947 = 0,691 - il limite superiore è l2 = 1,638 + 0,947 = 2,585
Per ritornare alla
stessa scala del rapporto (RR = 3,929) si deve calcolare l’antilog; i due
limiti calcolati diventano l’esponente di - per il limite
inferiore, - per il limite
superiore, In conclusione, il rischio relativo calcolato con i dati sperimentali è RR = 3,929. L’intervallo di confidenza del valore reale è compreso tra 1,996 e 13,263 con probabilità del 95% di affermare il vero.
La misura di rischio relativo (RR) e l’introduzione al concetto di odds ratio è attribuita a J. Cornfield per uno studio su dati clinici del 1951 (vedi l’articolo A method of estimating comparative rates from clinical data. Applications to cancer of the lung, breast and cervix, pubblicato su Journal of the National Cancer Institute, Vol. 11, pp. 1229 – 1275). Per chiarire i concetti e meglio comprendere i metodi, è utile rivedere la presentazione del suo articolo, molto chiara e semplice. E’ utile soprattutto per evitare una trappola logica, in cui è facile cadere quando non si inizia questo tipo di ricerche. Nella ricerca epidemiologica, un problema frequente è determinare la probabilità di essere colpiti da una malattia specifica, sulla base di una precisa caratteristica comportamentale; per esempio, ammalarsi di cancro al polmone fumando un certo numero di sigarette al giorno. Teoricamente la soluzione è semplice: - su un campione di fumatori abituali, si rileva la proporzione (p1) di persone ammalate, - su un campione di non fumatori, della stessa età del campione precedente, si rileva la proporzione (p2) di persone ammalate; - la differenza (d) tra le due proporzioni (d = p1 – p2) misura l’intensità dell’associazione (the strength of association) tra fumo e cancro al polmone in quella età. Ma avere la proporzione degli ammalati di una malattia specifica (come il cancro al polmone), in varie categorie comportamentali (come l’essere fumatori abituali di sigarette) e/o in classi d’età (come in quella da 40 a 49 anni) non è frequente.
La ricerca epidemiologica spesso è fondata sulle cartelle cliniche. Delle persone colpite di cancro al polmone è noto se sono fumatori o no e la classe d’età. Da questi dati non si determina la proporzione di persone colpite dal cancro tra i fumatori e i non fumatori, ma solo la percentuale o proporzione di fumatori tra gli ammalati. La differenza delle frequenze relative dei fumatori e dei non fumatori tra gli ammalati non misura l’intensità dell’associazione tra malattia e fumo; quindi non si ha alcuna l’indicazione sul fatto che il fumo sia carcinogeno. Per ricavare da questi dati la proporzione di ammalati tra i fumatori (p1) e i non fumatori (p2) servono altre informazioni, raccolte con una impostazione corretta.
Un breve inciso sulla terminologia: in epidemiologia si misurano incidenza e prevalenza. Incidenza (incidence) è la proporzione di persone sane che sviluppano la malattia in un certo periodo di tempo (di solito l’anno o il mese); è la proporzione di nuovi ammalati: - Incidenza = numero di casi nuovi in un periodo / numero di persone a rischio nello stesso periodo
- Prevalenza (prevalence) è una misura della proporzione di persone ammalate in un certo periodo. Può essere misurata in modo puntiforme (point prevalence) oppure su un periodo (period prevalence). - Prevalenza = numero di ammalati / numero della popolazione
Misura l’esistenza di una malattia. E’ legato alla incidenza in quanto - Prevalenza = Incidenza x tempo medio di durata della malattia
| |
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |
e 
,
è il valore
di Z alla probabilità 
= 
= 10,97
quindi > 5 
= 
= 6,995
quindi > 5
e 
(dove e = 2,71828
approssimato alla 5 cifra decimale). Di conseguenza, i due limiti
dell’intervallo di confidenza del rapporto tra rischi RR sono:
= 2,718280,691 = 1,996
= 2,718282,585 = 13,263