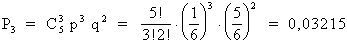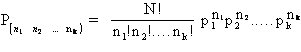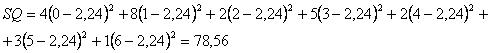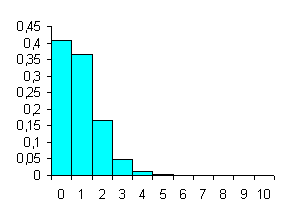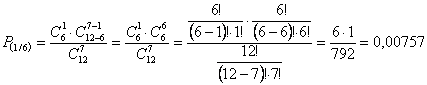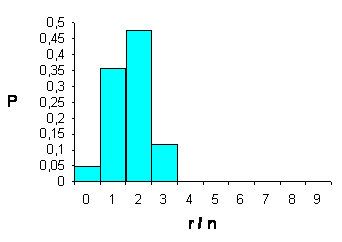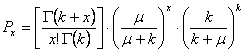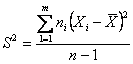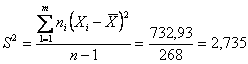DISTRIBUZIONI  e  leggi  di  probabilità'

 

 

 2.3.   ALCUNE DISTRIBUZIONI DISCRETE

 

 

Le variabili casuali hanno distribuzioni di probabilità di due tipi: discrete o continue. Negli esercizi precedenti, con il calcolo combinatorio, si sono stimate distribuzioni di probabilità discrete, che possono essere calcolate per un numero definito di casi. Nelle variabili casuali discrete, i valori argomentali sono i numeri naturali: 0, 1, 2, …, n. Servono per calcolare la probabilità di eventi che hanno un numero discreto di ricorrenze.

Una variabile casuale è continua quando la sua distribuzione è continua. Con tale variabile continua, si stima la probabilità di estrarre non un singolo valore ma valori ad esso uguali o maggiori (oppure minori). Una distribuzione continua non permette la stima della probabilità di estrarre un particolare valore, ma solo quelli compresi in un dato intervallo. Per esempio, nella distribuzione delle altezze di una popolazione di studenti, non è possibile stimare la probabilità di avere un individuo alto esattamente 176,000  cm ma quella di avere un individuo tra 180 e 190 centimetri.

 

 

2.3.1   Distribuzione binomiale

La binomiale è una distribuzione teorica discreta e finita, per eventi classificati con una variabile binaria. E’ denominata anche distribuzione di Bernoulli o distribuzione bernoulliana, in onore del matematico svizzero Jacques Bernoulli (1654-1705), che ha fornito importanti contributi alla teoria della probabilità.

In un collettivo di n unità che possono essere ripartite solo in due classi A e B, con frequenze assolute n_a e n_b, le cui frequenze relative sono p e q con

 

la probabilità di avere i volte l'evento A (e quindi n - i volte l'evento alternativo B) è data da

 

ricordando, dalle combinazioni semplici, che

 

La distribuzione binomiale o bernoulliana fornisce le risposte al problema delle prove ripetute: stima le probabilità che un evento, con probabilità a priori o frequentista p, avvenga rispettivamente 0, 1, 2,...i,...n volte, nel corso di n prove identiche ed indipendenti. Le prove possono essere successive oppure simultanee, purché siano tra loro indipendenti, non si influenzino reciprocamente e quindi le probabilità dei singoli eventi si mantengano costanti.

Le variabili casuali di tipo binario sono numerose: maschio/femmina, successo/insuccesso, malato/sano, inquinato/non inquinato, alto/basso, negativo/positivo. Inoltre tutte le variabili, sia le multinomiali sia quelle continue, possono sempre essere ridotte alla più semplice variabile dicotomica o binaria, seppure con perdita d’informazione. Per esempio, una popolazione classificata in individui di specie diverse (A, B, C, D, E, ...) può sempre essere ricondotta ad una classificazione binaria in specie A e specie non-A; una serie di misure con scala discreta o continua, non importa se di ranghi, d’intervalli o di rapporti, può sempre essere ricondotta ad una classificazione binaria di valori superiori (+) od inferiori ( -) ad un limite prefissato.

 

 

Esempio 1.  E' statisticamente dimostrato, anche se non è stata ancora trovata una spiegazione esauriente, che in tutte le popolazioni umane nascono più maschi che femmine, con un rapporto di 105-106 maschi ogni cento femmine. Possiamo quindi stabilire, a posteriori e sulla base di queste analisi, che la probabilità frequentista della nascita di un maschio è approssimativamente p = 0,52 e che quella di una femmina è, di conseguenza, q = 0,48 (q = 1 - p).

Usando la distribuzione binomiale, possiamo calcolare le specifiche probabilità P di avere 0, 1, 2, 3, 4  figli maschi nelle famiglie con 4 figli:

 

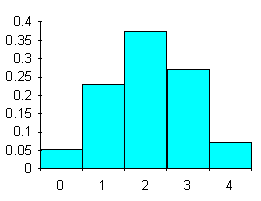
Se gli eventi sono casuali ed indipendenti e le probabilità di avere un maschio od una femmina sono costanti, in famiglie con 4 figli la probabilità

- P₀ di avere 0 figli maschi è 0,05 

- P₁ di avere 1 figlio maschio è 0,23

- P₂ di avere 2 figli maschi è 0,37

- P₃ di avere 3 figli maschi è 0,28

- P₄ di avere 4 figli maschi è 0,07.

 

Non esistono altri eventi possibili oltre quelli calcolati; di conseguenza, il totale delle probabilità stimate deve necessariamente essere uguale a 1 (0,05 + 0,23 + 0,37 + 0,28 + 0,07 = 1,00); è prassi che gli arrotondamenti siano tali da dare sempre una somma uguale a 1,00.

 

La rappresentazione grafica di queste probabilità

 

Figura 1.  Probabilità del numero di maschi in famiglie con 4 figli.

 

mediante istogramma mostra con evidenza una distribuzione leggermente asimmetrica. La causa è il differente valore dei due eventi alternativi (p = 0,52; q = 0,48) e del numero basso di eventi (n = 4). Se le probabilità p e q fossero state uguali (ovviamente entrambe 0,5) la distribuzione sarebbe stata simmetrica; con p e q diversi, diventa simmetrica all’aumentare del numero di dati, come sarà di seguito dimostrato empiricamente.

 

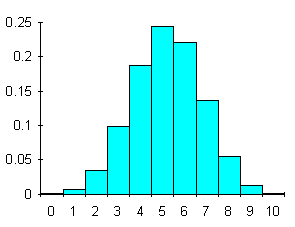
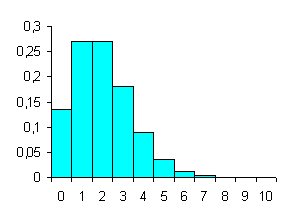
ESEMPIO 2. Applicando la stessa legge, in eventuali famiglie con 10 figli le probabilità P(i) di avere i figli é

 

 

La sua rappresentazione grafica con un istogramma è:

 

 

Figura 2.  Probabilità del numero di maschi in famiglie con 10 figli

 

 

Essa evidenzia meglio della tabella la presenza di una leggera asimmetria.

La distribuzione di probabilità della binomiale dipende da 2 parametri: p e n.

Se p e q sono uguali a 0,5 la distribuzione è sempre simmetrica, indipendentemente da n. Se p è molto più grande o più piccolo di q, la distribuzione è asimmetrica, ma l’asimmetria tende a diminuire al crescere di n.

Di norma, si ricorre alla distribuzione binomiale per valori di p che variano da 0,1 a 0,9. Per valori di p esclusi da questo intervallo si ricorre alla distribuzione poissoniana, quando n non è grande. Quando n è così grande che anche n×p è grande, si ricorre comunque alla normale, per qualsiasi valore di p.

Quando un campione è di grandi dimensioni, la stima delle probabilità è ottenuta dalla distribuzione normale. A tal fine è intuitivo che in una distribuzione binomiale la media della popolazione se calcolata come frequenza assoluta è n×p

m = n×p

 

mentre, se calcolata come frequenza relativa, è

m = p

 

Per esempio, in famiglie di 10 figli il numero medio di maschi è 10 x 0,52 = 5,2 in frequenza assoluta e 0,52 in frequenza relativa.

Senza ricorrere alla dimostrazione, che sarebbe lunga, è ugualmente importante ricordare che la varianza s² della popolazione in frequenza assoluta è data dal prodotto di  n×p×q

s² = n×p×q

mentre in una frequenza relativa è

s² =p×q / n

I rapporti tra media e varianza offrono indicazioni importanti, quando dai dati sperimentali sia necessario risalire alla più probabile legge di distribuzione che li hanno determinati.

Nella distribuzione binomiale la varianza è inferiore alla media:

- con una media  uguale a n×p e una varianza  uguale a n×p×q,

- poiché p + q è uguale a 1 ed il valore di q è inferiore a 1,

- il valore di n×p×q è inferiore a n×p.

 

 

ESERCIZIO  1.  La distribuzione binomiale è utile anche nei casi in cui le probabilità sono note a priori, come nel lancio di dadi non truccati. Lanciando un dado 5 volte, quale è la probabilità di avere 3 volte il numero 1?

 

Risposta: (n = 5;  i = 3;  p = 1/6;  q = 5/6)

 

 

ESERCIZIO  2.  In un'urna contenente un numero elevatissimo, praticamente infinito, di biglie nel 70% nere e per il rimanente 30% bianche, quale è la probabilità di estrarre 4 biglie  tutte nere?

 

Risposta: (n = 4;  i = 4;  p = 0,7;  q = 0,3)

 

 

ESERCIZIO  3.  Un esperimento di laboratorio di solito risulta positivo nel 20% dei casi. Con 10 tentativi quale è la probabilità che 9 risultino positivi e 1 solo negativo?

 

Risposta: (n = 10;  i = 9;  p = 0,2;  q = 0,8)

 

 

ESERCIZIO  4.  In un lago, la specie A rappresenta il 33% degli individui presenti, la specie B  e C entrambi il 25% e la specie D il 17%; estraendo a caso 15 individui, quale è la probabilità che

a) nessuno sia della specie A, 

b) tutti siano della specie A

c) almeno 10 siano della specie A

d) meno di 7 siano della specie A

Risposte :

 

a) la probabilità che nessuno sia della specie A è 0,002461: vedi P₍₀₎ nella tabella sottostante;

b) la probabilità che tutti siano della specie A è minore di 1 su 1 milione di casi : vedi P₍₁₅₎

c) la probabilità complessiva che almeno 10 dei 15 individui estratti a caso siano della specie A è data dalla somma delle probabilità calcolate per  P₍₁₀₎, P₍₁₁₎, P₍₁₂₎, P₍₁₃₎, P₍₁₄₎ e P₍₁₅₎;

d) la probabilità complessiva che meno di 7 individui siano della specie A è data dalla somma delle singole probabilità da P₍₀₎ a P₍₆₎ compresi.

 

 

i	P(i)
0	0.002461
1	0.018183
2	0.062689
3	0.133798
4	0.197702
5	0.214226
6	0.175858
7	0.111364
8	0.054851
9	0.021013
10	0.00621
11	0.00139
12	0.000228
13	0.000026
14	0.000002
15	0.000000

 

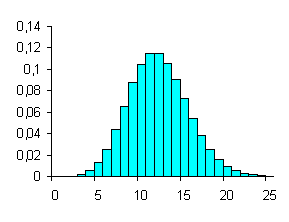
Tabella 2.  Distribuzione binomiale con n = 15   e   p = 0.33

 

 

L’istogramma delle probabilità da P₍₀₎ a P₍₁₅₎ mostra come la distribuzione sia già approssimativamente normale, benché la probabilità di ogni singolo evento  si discosti da 1/2.

 

 

Figura 3.  Istogramma della distribuzione binomiale con n = 15  e   p = 0.33

 

 

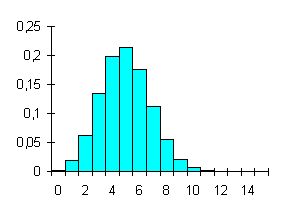
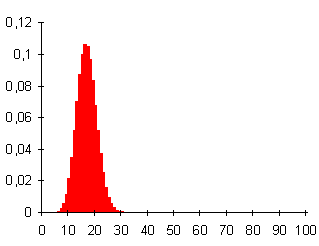
ESERCIZIO  5.  Per dimostrare come all’aumentare del numero di osservazioni la distribuzione diventi simmetrica e pertanto come essa possa essere bene approssimata da una distribuzione normale,  chi è in grado di usare e programmare un calcolatore stimi tutte le probabilità possibili con p = 1/6 e n = 100, ovviamente con i che varia a 0 a 100.

 

Risposta.   Le probabilità associate ai diversi tipi di estrazione possono essere espresse anche dai termini dello sviluppo del binomio  . La loro rappresentazione grafica, riportata nel grafico sottostante, evidenzia come la distribuzione abbia forma molto simile alla normale, causa dell’alto valore di n benché p sia lontano da 0,5.

 

Figura 4.  Istogramma della distribuzione binomiale con n = 100  e  p = 1/6

 

2.3.2   DISTRIBUZIONE MULTINOMIALE

La distribuzione multinomiale rappresenta una estensione di quella binomiale; si applica a k eventi indipendenti di probabilità p₁, p₂, ...p_i, ..., p_k (la cui somma è uguale a 1) che possono comparire nel corso di N prove indipendenti, successive o simultanee.

Permette di calcolare la probabilità di ogni evento possibile, quando determinato solo dal caso.

 

La probabilità che si realizzino congiuntamente tutti gli eventi indicati è determinata dallo sviluppo del multinomio:

 

 

 

ESEMPIO.   Si supponga che in un lago, con un numero teoricamente infinito di pesci, il 10% (p₁ = 0,10) siano della specie A,  il 40% (p₂ = 0,40) siano della specie B,  il 20% (p₃ = 0,20) siano di quella C ed il 30% (p₄ = 0,30) della specie D;

a) estraendo 10 pesci, quale è la probabilità di avere 2 A, 3 B, 2 C e 3 D?

b) estraendo 8 pesci quale è la probabilità di avere 4 B e 4 D? (naturalmente con 0 A e 0 C).

 

Risposte:

a) La probabilità di estrarre 2 individui della specie A, 3 della specie B, 2 della specie C e 3 della specie D, in un lago in cui le quattro specie hanno le frequenze relative della domanda, è calcolata con

 

 

e risulta uguale a 0,0174 o 1,74 per cento.

 

b) La probabilità di estrarre per caso, dallo stesso lago, 4 individui della specie B e 4 della specie D con 8 estrazioni casuali è

 

uguale a 0,0145 o 1,45 per cento.

Non esiste un limite al numero di fattori che possono essere considerati insieme.

La distribuzione binomiale è utilizzata con frequenza nella statistica non parametrica. Se il numero di dati è ridotto, molti test non parametrici ricorrono ad essa per il calcolo delle probabilità.

Seppure apparentemente più generale, la distribuzione multinomiale ha un uso limitato, circoscritto alla stima della probabilità complessiva di più eventi indipendenti, per ognuno dei quali sia nota la probabilità p_i.

 

 

2.3.3   DISTRIBUZIONE POISSONIANA

Quando il numero di dati (n) è molto grande e la probabilità (p) è molto piccola, la distribuzione binomiale presenta vari inconvenienti pratici, che erano importanti soprattutto prima dell'introduzione del calcolo automatico. Infatti, essa richiede sia l'innalzamento di probabilità (p) molto basse a potenze (i) elevate, sia il calcolo di fattoriali per numeri (n) grandi, che sono operazioni che rendono il calcolo manuale praticamente impossibile.

Per

-   n che tende all'infinito, 

-   p che tende a 0,

-   in modo tale che n×p sia costante,

 il matematico francese Siméon Dennis Poisson (1781-1840), già autore di articoli sulla meccanica celeste e sull’elettromagnetismo, nel 1837 entro la sua opera maggiore Recherches sur la probabilité des jugements en matière criminelle et en matière civile ha dimostrato che la probabilità dell’evento (P_i) è stimata da

  

 con e = 2,71828.

 

In modo più semplice per i calcoli, la stessa formula può essere scritta

 come

 

La poissoniana è una distribuzione teorica discreta, totalmente definita da un solo parametro: la media m, quando riferita a una popolazione, che deve essere costante. Quando la distribuzione è applicata a un campione, la media m è sostituita da quella campionaria .

Anche nella distribuzione poissoniana, la media attesa  è data dal prodotto n×p, con (p + q) = 1. Poiché, come in tutte le distribuzioni che possono essere fatte derivare dalla binomiale, s²= n×p×q, è facile dimostrare come la varianza sia uguale alla media (s² = m). Applicando le tre condizioni appena enunciate,

-  n che tende all’infinito,

-  p che tende a 0,

- p + q  = 1

 la varianza della distribuzione di Poisson è

 

 

In termini discorsivi,

 con un numero infinito di dati, se p tende a 0 e quindi q tende a 1, la varianza è uguale alla media

n×p×q (s²) = n×p (m).

E’ un concetto importante quando si deve individuare la forma reale di una distribuzione campionaria.

La legge di distribuzione poissoniana è detta anche legge degli eventi rari, poiché la probabilità (p) che l’evento si verifichi per ogni caso e la media (m) degli eventi su tutta la popolazione sono basse. E’ chiamata pure legge dei grandi numeri, in quanto tale distribuzione è valida quando il numero (n) di casi considerati è alto.

 

Nella pratica della ricerca, la distribuzione poissoniana sostituisce quella binomiale quando p < 0,05  e  n > 100.

 

La distribuzione poissoniana è utilizzata per eventi che si manifestano sia nello spazio che nel tempo.

E’ il caso del numero di insetti presenti in una superficie di piccole dimensioni o del numero di eventi che possono avvenire in un breve intervallo di tempo. In molti testi, il numero medio di eventi è indicato non con m ma con l, in particolare quando si tratta di eventi temporali.

 

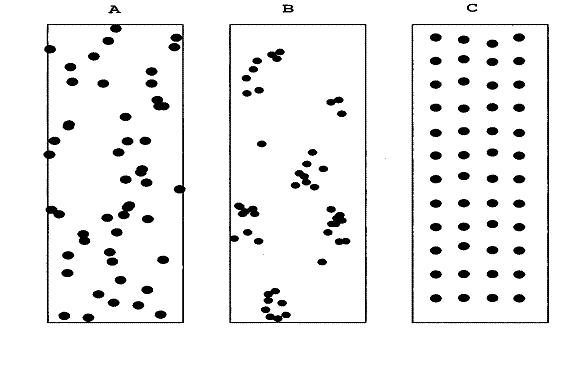
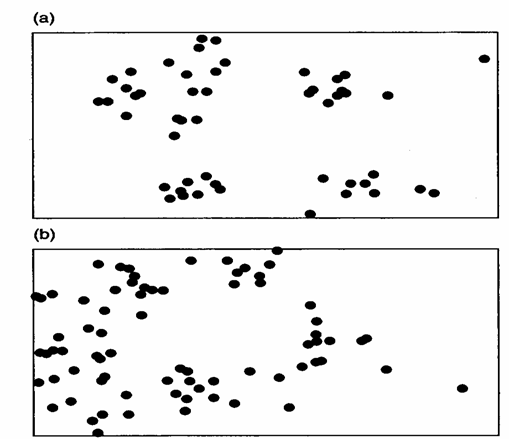
Casuale                                      Aggregata                                     Regolare

 

Figura 5. Tipi semplici di distribuzione spaziale degli individui di una popolazione

 

 

Considerando lo spazio, più facile da rappresentare e caso più frequente nella ricerca biologica e ambientale, una distribuzione di oggetti segue la legge poissoniana quando è casuale (in inglese  random).

 

Le figura precedente illustra i tre tipi fondamentali di distribuzione di una specie o di una comunità su un territorio.

In modo schematico, può avare tre tipi principali di aggregazione:

A -  distribuzione casuale (random),

B -  distribuzione aggregata (aggregated) o a gruppi,

C -  distribuzione uniforme (uniform) o regolare.

Dalla loro diversa combinazione deriva un numero infinito di possibilità:

 

 

 

Tabella 5.  Distribuzione di Poisson con , per  che varia da 0 a 25

 

 

La distribuzione poissoniana ha una forma molto asimmetrica, quando la media è piccola.

Quando µ < 1, la classe più frequente o più probabile è zero.

E’ ancora asimmetrica per valori di µ < 3. Ma già con µ ³ 5-6 la distribuzione delle probabilità è vicina alla forma simmetrica e può essere bene approssimata dalla distribuzione normale o gaussiana.

 

Le probabilità di una distribuzione poissoniana con m = 12 è quasi perfettamente simmetrica, come mostra la tabella precedente e evidenzia ancor meglio il grafico successivo di distribuzione delle probabilità  (sull’asse delle ordinate), per i diversi valori di  (sull’asse delle ascisse)

 

 

Figura 6.  Distribuzione di Poisson con .

 

 

In termini tecnici, si dice che per avere una distribuzione poissoniana, una variabile casuale deve avere tre requisiti: stazionarietà, non-multiplicità, indipendenza.

 

Si ha

1 -  omogeneità  o stazionarietà quando la media m (o la probabilità p) dell’evento è costante, su tutto il periodo considerato o l’area in osservazione; in altri termini, quando la probabilità di ogni evento in un intervallo di tempo (t, t + h) o in uno spazio infinitesimo è costante, pari a lh per ogni t;

2 -  individualità  o non-multiplicità quando gli eventi avvengono singolarmente, non a coppie o a gruppi; in tali condizioni, la probabilità che due o più eventi avvengano nello stesso intervallo infinitesimo di tempo o di spazio non è lh volte minore di quello di un solo evento;

3 -  indipendenza quando il presentarsi di un evento, in una particolare unità di tempo o di spazio, non influenza la probabilità che l’evento si ripresenti in un altro istante o luogo.

Tutti questi concetti, evidenziati nelle figure, sono sinteticamente compresi nell’espressione che i fenomeni non devono essere né contagiosi, né regolari.

 

ESEMPIO 1  (PER VALUTARE SE UNA DISTRIBUZIONE E’ POISSONIANA, tratto con modifiche dal testo di Charles J. Krebs del 1999, Ecological Methodology, 2^nd ed. Benjamin/Cummings, Addison Wesley Longman, Menlo Park, California, p. X + 620).

Una superficie, come una delle tre figure precedenti, è stata suddivisa in 25 quadrati delle stesse dimensioni e in ognuno è stato contato il numero di organismi della specie X con il seguente risultato

 

 

 

E’ una distribuzione casuale?. In altri termini, il numero di organismi in ogni quadrato segue la legge di Poisson?

 

Risposta. Come prima parte dell’analisi, dalla serie dei 25 dati

- costruire la distribuzione di frequenza,

- calcolare la media,

- calcolare la varianza.

 

Osservando che il valore minimo è 0 e il valore massimo è 6,

-  la distribuzione di frequenza è

 

 

 

Da essa si ricavano

-  la media dei 25 valori

 

 che risulta  = 2,24 e

 

- successivamente la devianza

 che risulta SQ = 78,56

 e infine  la varianza

 che risulta .

Risulta immediatamente che la varianza (3,273) è maggiore della media (2,24).

 

In tale situazione (), la prima indicazione è che la distribuzione non è perfettamente poissoniana, quindi non è casuale, ma è tendenzialmente aggregata: gli individui tendono a distribuirsi sul terreno a gruppi.

Se la varianza fosse stata inferiore alla media, la distribuzione sarebbe stata ugualmente non casuale, ma perché troppo regolare: la popolazione sarebbe stata distribuita in modo tendenzialmente uniforme.

 

Tuttavia il campione è piccolo. Ne deriva che la differenza rilevata tra media e varianza può essere dovuta non a un fenomeno reale, ma alle variazioni casuali, sempre sono sempre molto importanti quando il numero di osservazioni è limitato, come in questo caso.

 

Per un valutazione più approfondita, dalla sola conoscenza della media è utile ricavare tutta la distribuzione teorica del numero di individui per quadrato.

Mediante la formula della distribuzione poissoniana

 

 con = 2,24 e  che varia da 0 a 6

 si ricava la seguente serie di probabilità:

 

 

 

 

In modo più dettagliato, da  = 0  a    = 6 le singole probabilità sono calcolate direttamente con

 

 

L’ultima, indicata con  ³ 7 e uguale a 0,0081, è ricavata per differenza da 1,00 della somma di tutte le probabilità  precedenti (0,9919).

 

Infine,

-  si ottiene la frequenza attesa per ogni  (riportata nella terza riga della tabella sottostante),

-  moltiplicando la probabilità stimata  

-  per il numero totale  di  rilevazioni.

 

In questo caso, il numero totale di individui è  = 25.

 

 

Osservando la tabella, la prima domanda che un ricercatore si deve porre è: “La distribuzione osservata (seconda riga) è in accordo con quella attesa? (terza riga)”

Per rispondere in modo scientifico, senza limitarsi alla semplice impressione, occorre applicare un test. Si dovrebbe quindi  passare all’inferenza, i cui metodi sono presentati nei capitoli successivi.

 

 

ESEMPIO 2. Tassi elevati di inquinamento atmosferico possono determinare reazioni allergiche gravi. Durante un mese (30 giorni), nel pronto soccorso di un ospedale si sono avuti 27 ricoveri urgenti. Può essere ragionevole ipotizzare che gli eventi abbiano una distribuzione giornaliera costante, in accordo con la legge di Poisson.

Calcolare la probabilità () di avere  casi di allergia al giorno, per  che varia da 0 a 8.

Risposta.  Dopo aver calcolato la media giornaliera 0,9 (27/30),

 si applica la formula

 =

 

e si ottengono i risultati riportati nella tabella

 

0	0.40657
1	0.365913
2	0.164661
3	0.049398
4	0.011115
5	0.002001
6	0.000300
7	0.000039
8	0.000004

 

Tabella 3.  Distribuzione di Poisson con  .

 

 

Se la distribuzione fosse esattamente casuale, nel 40% dei giorni non si dovrebbe avere nessun caso; si dovrebbe avere 1 solo ricovero nel 36,6% e 2 ricoveri nel 16,5% dei giorni.

 

La rappresentazione grafica

 

 

Figura 7.  Distribuzione di Poisson con .

 

 

 evidenzia come la distribuzione delle probabilità con m = 0,9 sia fortemente asimmetrica, con asimmetria destra.

 

 

ESEMPIO 3. E’ stato ipotizzato che gli individui della specie A abbiano una distribuzione poissoniana sul terreno. Dividendo l’area campionata in appezzamenti della stessa dimensione, per superficie unitaria si è ottenuto  = 2,0.

Calcolare la frequenza attesa (), per  che va da 0 a 5. in una distribuzione poissoniana.

 

Risposta: Il calcolo delle frequenze relative è

 

 

0	0.135335
1	0.270671
2	0.270671
3	0.180447
4	0.090224
5	0.036089

 

Tabella 4.  Distribuzione di Poisson con

 

Come mostra il grafico successivo, la forma della distribuzione poissoniana con media uguale a 2 è ancora asimmetrica, seppure in modo molto meno accentuato della distribuzione precedente, che aveva una media inferiore. L’asimmetria è sempre destra o positiva, fino a quando la distribuzione diviene normale e simmetrica.

 

Figura 8.  Distribuzione di Poisson,

 

 

ESEMPIO 4.   In letteratura come esempio storico della distribuzione poissoniana, tratta da dati sperimentali, è famoso l’esempio di Ladislaus von Bortkiewicz (1868 – 1931, a volte scritto all’inglese come Bortkiewitch). Prendendo i dati dell’armata prussiana del XIX secolo, per 20 anni ha contato in 10 corpi d'armata il numero di soldati che ogni anno morivano a causa di un calcio di mulo; ha quindi classificato i decessi nei 200 eventi (20 corpi d'armata per 10 anni), ottenendo la tabella sottostante:

 

 

Tabella 6.  Morti per corpo d'armata e per anno, rilevati da Bortkewicz.

 

 

Come riportato in essa,

-  in 109 casi non si è avuto nessun morto,

-  in 65 casi si è avuto 1 morto,

-  in 22 casi sono stati contati 2 morti,

-  in 3 casi 3 morti

-  e in 1 caso 4 morti.

In totale, nei 200

109 + 65 + 22 + 3 + 1 = 200

casi esaminati il numero di morti è stato di 122

109 x 0 + 65 x 1 + 22 x 2 + 3 x 3 + 1 x 4 = 122

Il calcolo della media e della varianza, secondo le formule presentate nel primo capitolo sulle distribuzioni di frequenza, fornisce i seguenti risultati:

media = m = 122/200 = 0,6100

varianza = s ² = 0,6079

 

E’ importante osservare che la varianza di questa distribuzione sperimentale è quasi identica alla sua media, come atteso in una distribuzione poissoniana teorica. E’ una buona indicazione che questi eventi seguono la legge di Poisson; ma la dimostrazione più completa è fornita dal confronto tra la distribuzione attesa e quella osservata.

 

Applicando la distribuzione di Poisson, si determinano le probabilità teoriche di avere ogni anno per corpo d'armata 0 morti, 1 morto,..., n morti, eseguendo i calcoli sottostanti (approssimati rispetto alle possibilità attuali di calcolo)

 

 

 

 

 

Le probabilità stimate sono riferite ad ogni corpo d’armata in un anno. Si ottengono i relativi eventi attesi rapportandole a 200 casi (20 corpi d’armata per 10 anni).  

 

 

 

Tabella 7.  Eventi osservati ed eventi attesi per corpo d'armata e per anno.

 

 

Il problema reale del confronto con un test tra le frequenze attese e quelle osservate consiste nel capire se le differenze sono di entità trascurabile, puramente imputabili al caso, oppure se sono di entità tale da lasciare presupporre l’intervento di leggi o fattori diversi da quelli ipotizzati nella distribuzione teorica.

 

 

2.3.4   DISTRIBUZIONE GEOMETRICA E DISTRIBUZIONE DI PASCAL

La distribuzione binomiale serve per valutare, entro un numero complessivo n di eventi, la probabilità P di avere i eventi favorevoli (P_i), ognuno dei quali ha una probabilità p costante. Con n prefissato (esempio: famiglie di 4 figli) e p costante (esempio: la probabilità p = 0.52 di avere un figlio maschio), permette di stimare la probabilità di avere i volte l’evento atteso (esempio: avere 0 oppure 1  oppure 2, 3, 4 figli maschi). Nel calcolo, n e p sono costanti, mentre i varia.

 

La distribuzione geometrica serve per valutare la probabilità di avere un evento favorevole (i = 1). Con i prefissato (uguale a 1) e p costante, permette di stimare la probabilità (P_n) di avere l’evento desiderato all’aumentare del numero n di osservazioni. Nel calcolo della distribuzione geometrica, i e p sono costanti mentre n varia. 

 

Ad esempio, si supponga che, in un’analisi complessa di laboratorio, un esperimento abbia il 30% di probabilità di dare una risposta positiva. Quante prove occorre fare per avere la probabilità P di avere una risposta positiva?

 

La probabilità che il primo tentativo sia positivo è p. Scritto in modo formale:

P(N = 1; p) = p

 

La probabilità che il secondo tentativo dia un risultato positivo è (1- p) x p:

P(N = 2; p) = (1 – p) × p

 

La probabilità che sia il terzo a dare il risultato positivo è

P(N = 3; p) = (1 – p)² × p

 

e la probabilità che sia l’n-esimo è

P( N = n; p) = (1 – p)^{n - 1} × p

 

 

ESEMPIO. Con p = 0,3 calcolare la probabilità P di avere l’evento desiderato alle prove da 1 a n.

 

Risposta. Sviluppando

P(n) = (1 – p)^{n - 1} × p

 si ottengono le probabilità riportate nella tabella

Ad esempio, con n = 3 la probabilità è

 

 

 

Ottenuti mediante la formula sopra riportata, i valori della tabella sono le probabilità (i dati del calcolo nella colonna 2, i risultati nella colonna 3) che l’esperimento riesca al primo tentativo, al secondo e così via. Sono probabilità esatte: forniscono la probabilità che ogni singolo tentativo dia la risposta desiderata.

Se è necessario sapere quanti tentativi occorre fare, per avere una determinata probabilità che entro essi sia presente almeno una risposta positiva, si deve utilizzare la sommatoria dei singoli valori esatti. L’elenco della tabella mostra che per avere una probabilità non inferiore al 90%  di avere il primo risultato positivo occorre fare 7 tentativi, mentre per una probabilità non inferiore al 95%  occorre fare 9 tentativi, sempre che la probabilità sia costante e gli eventi siano indipendenti. 

 

La distribuzione di Pascal (Blaise Pascal matematico e filosofo francese, nato nel 1623 e morto nel 1662) è la generalizzazione della distribuzione geometrica: supponendo una probabilità p costante per ogni evento atteso, serve per valutare la probabilità che entro n osservazioni sequenziali sia compreso i volte l’evento atteso (con i che può essere uguale a 1, 2, 3, …, n) .

La precedente distribuzione geometrica è un caso della distribuzione di Pascal, con i = 1.

 

Se ogni evento ha una probabilità p costante ed indipendente, la probabilità che esso avvenga i volte all’aumentare del numero n di osservazioni è

 

P(N = n; i; p) = 

 

Dove, ovviamente, n ³ i (la cui interpretazione è: per avere 3 risultati simultaneamente positivi, occorre fare almeno 3 prove).

 

 

ESEMPIO. Si supponga che, in una popolazione animale allo stato selvatico, il 40% degli individui (p = 0,4)  sia colpito da una malattia; per una serie di analisi più approfondite e proporre la cura servano 3 animali ammalati. Quanti occorre catturarne, con un campionamento sequenziale, per avere i 3 individui ammalati ad una probabilità prefissata?

 

Risposta:  Con i dati dell’esempio, i = 3   e    p = 0,4

 la formula generale diventa

P(N = n;   3;  0,4) = 

 

 con n che aumenta progressivamente a partire da 3.

 

Con n = 7, il calcolo della probabilità di trovare tra essi 3 ammalati è

 

uguale a 0,124416 o 12,44%

Nella tabella è stato riportato il calcolo delle probabilità con n che varia da 3 a 12:

 

 

 

 

Se si catturano 3 animali, la probabilità che tutti e tre siano ammalati è uguale a 6,4 per cento.

Catturando un quarto animale, la probabilità che esso possa essere il terzo ammalato è di 11,52% e la probabilità complessiva di avere almeno i tre ammalati che servono diventa 17,92 %.

Infine, con il dodicesimo animale catturato, la probabilità di averne entro essi almeno tre ammalati è superiore al 90%, esattamente uguale a 91,6555 per cento.

 

L’esempio serve anche per risolvere altri tipi di problemi, quale la frequenza reale di ammalati nella popolazione da cui si estrae il campione. 

Se, con un numero elevato di animali catturati (esempio 30), non è stato possibile selezionare i 3 individui ammalati, deve sorgere il sospetto che la percentuale di ammalati in realtà sia nettamente inferiore al 40 per cento stimato. Per esempio, si supponga che con 15 animali la probabilità cumulata superi il 95%; se con 15 animali catturati non si fosse ancora raggiunto il numero di 3 ammalati, si potrebbe ragionevolmente pensare che la frequenza p di ammalati sia minore di 0,4. Tale affermazione avrebbe una probabilità di oltre il 95% di essere vera e quindi inferiore al 5% di essere falsa.

 

Se con la distribuzione di Pascal si conta il numero di insuccessi avuti prima di arrivare al numero desiderato di casi postivi, si ottiene una distribuzione simile alla distribuzione binomiale negativa (che sarà presentata in un paragrafo successivo).

 

2.3.5   DISTRIBUZIONE IPERGEOMETRICA

Nella distribuzione binomiale, presa come riferimento per tutte le distribuzioni teoriche presentate, la probabilità p di un evento è costante. Quando la probabilità p di una estrazione casuale varia in funzione degli eventi precedenti, come succede in una popolazione limitata e di piccole dimensioni, si ha la distribuzione ipergeometrica.

 

Un modo semplice per chiarire la differenza tra distribuzione binomiale e distribuzione ipergeometrica è fornito dal gioco delle carte, con il calcolo delle probabilità nell’estrazione di un secondo re da un mazzo di 40 carte, in funzione delle regole stabilite.

Il gioco può avvenire in due modi: (A) con reimmissione o (B) senza reimmissione della carta estratta.

 

 A- Con reimmissione: la probabilità di estrarre un re la prima volta è uguale a 4/40 o 1/10. Se la carta viene reintrodotta nel mazzo, la probabilità che la seconda carta sia un re rimane 1/10; in queste estrazioni, la probabilità di tutte le carte è sempre P = 0,1.

 

B- Senza reimmissione: la probabilità che la seconda carta sia un re dipende dalla prima estrazione.

a)  Se la prima carta era un re, la probabilità che la seconda lo sia è di 3/39, quindi P = 0,077;

b)  se la prima  carta non era un re, la probabilità che la seconda lo sia è di 4/39, quindi P = 0,103

Per la seconda carta e quelle successive, la probabilità P varia in funzione di quanto è avvenuto nelle estrazioni precedenti.

 

Da questo esempio è facile comprendere che, se il mazzo di carte fosse molto grande (n grande), la probabilità P rimarrebbe approssimativamente costante. Ne deriva che quando il campione è grande, la distribuzione binomiale rappresenta una buona approssimazione della ipergeometrica, che è una distribuzione tipica delle popolazioni piccole.

 

Nella distribuzione ipergeometrica, la probabilità di un evento (P) dipende da vari parametri, che devono essere tenuti in considerazione nel rapporto tra combinazioni:

 

 dove:

-  N = numero totale degli individui del campione (è un conteggio, quindi è un numero intero positivo);

-  n₁ = numero degli individui del campione che possiedono il carattere in oggetto (è un intero positivo, al massimo uguale a N);

-  n  = numero di individui estratti dal campione (è un numero intero non negativo, che al massimo può essere uguale a N);

-  r = numero degli individui che presentano il carattere in oggetto tra quelli estratti (è un numero intero non negativo, che al massimo può essere uguale al minore tra n e n₁).

 

La formula presentata può essere spiegata con un semplice ragionamento logico, fondato sul calcolo combinatorio.

Si supponga che un'urna contenga N biglie, delle quali n₁ bianche e N - n₁ nere; inoltre, si supponga che si estraggano dall'urna n biglie (con ) senza reintroduzione. Si vuole determinare la probabilità P(r/n) che delle n biglie estratte r siano bianche (con ).

Il calcolo delle varie probabilità richiede 4 passaggi logici:

1 - delle N biglie n possono essere estratte in  modi differenti,

2 - delle n₁ biglie bianche r possono essere estratte in  modi differenti,

3 - delle N - n₁ biglie nere, n - r possono essere estratte in  modi differenti,

4 - ognuna delle  diverse possibilità di estrazione delle biglie bianche si combina con ognuna delle   possibilità d'estrazione di biglie nere.

 

Da queste probabilità deriva la formula

 

 

ESEMPIO 1. Per la cura di una malattia rara molto grave, presso una struttura ospedaliera sono stati ricoverati 12 pazienti, di cui 7 femmine e ovviamente 5 maschi.  Dei 12 ammalati 6 sono guariti e 6 sono deceduti. L’osservazione dimostra che tra i 6 deceduti erano compresi tutti i maschi e una sola femmina.

E’ statisticamente fondato il sospetto che tale cura possa essere idonea per le femmine, ma assolutamente dannosa per i maschi?

 

Risposta.  Per impostare il calcolo combinatorio, è necessario attribuire i 4 gruppi in modo corretto:

1 – totale ammalati ricoverati: N = 12

2 – totale ricoverati morti: n = 6

3 – numero di femmine tra i ricoverati: n₁ = 7

4 – numero di femmine tra i deceduti: r = 1

 

Con la formula della distribuzione ipergeometrica

 si ottiene

 

 che la probabilità che tra i 6 decessi su 12 ricoverati una sola fosse femmina per il solo effetto del caso è minore dell’otto su mille (P_1/6 =  0,00757).

 

Lo stesso calcolo poteva essere impostato sui maschi. Quale è la probabilità che tra i sei deceduti fossero compresi i 5 maschi per solo effetto del caso?

I dati sarebbero diventati:

1 – totale ammalati ricoverati: N = 12

2 – totale ricoverati morti: n = 6

3 – numero di maschi tra i ricoverati: n₁ = 5

4 – numero di maschi tra i deceduti: r = 5

 e la stima della probabilità

 

 avrebbe ovviamente dato un risultato identico (P_5/6 = 0,00757), trattandosi dello stesso caso.

 

ESEMPIO 2. Con gli stessi dati dell’esempio 1, quale la probabilità se tra i decessi ci fossero stati 4 maschi? Inoltre stimare le probabilità per tutte le 6 possibili risposte.

 

Risposta. Con

1 – totale ammalati ricoverati: N = 12

2 – totale ricoverati morti: n = 6

3 – numero di maschi tra i ricoverati: n₁ = 5

4 – numero di maschi tra i deceduti: r = 4

 

 

 la probabilità sarebbe stata superiore a 11%.

 

Mentre nella prima risposta si poteva avere un dubbio ragionevole che il farmaco non fosse ugualmente efficace per femmine e maschi, in questo caso la probabilità  (P_4/6 > 11%) è alta, quindi tale da poter essere ritenuta casuale.

 

Nello stesso modo si possono stimare tutte le 6 possibili risposte:

 

 

 

Tabella 8. Probabilità di avere per caso il numero r di maschi tra i 6 decessi.

 

 

In questo caso la distribuzione delle probabilità è simmetrica e il suo totale, come ovvio, è uguale a 1 non esistendo altre possibili risposte.

 

 

ESEMPIO 3.   In una riserva di piccole dimensioni sono cresciuti 9 cinghiali, di cui 3 sono femmine (e ovviamente 6 sono maschi). Per ridurre il loro numero, è stata decisa una battuta di caccia, durante la quale sono stati abbattuti 5 animali, senza che vi sia stata la possibilità di fare attenzione al sesso. E' possibile stimare le diverse probabilità che nel gruppo degli animali uccisi siano compresi  animali dei due sessi nei vari rapporti possibili.

Nel caso dell’esempio, le domande possono essere:

a)  Quale è la probabilità che vengano uccise tutte le femmine?

b)  Quale è la probabilità che resti una sola femmina?

c)  Quale quella che sia uccisa una sola femmina?

d)  Quale quella che sopravvivano tutte e 3 le femmine?

 

Risposta.   Per impostare il calcolo combinatorio, è necessario attribuire i 4 gruppi in modo corretto:

1 - totale animali presenti: N = 9

2 - totale animali uccisi: n = 5

3 - femmine presenti: n₁ = 3

4 - femmine uccise: r    a) = 3;  b) = 2; c) = 1; d) = 0.

Il calcolo delle probabilità è riportato nella tabella

 

R	P
0	0.047619
1	0.357143
2	0.47619
3	0.119048

 

Tabella 9.  Probabilità di eliminare le r femmine su 9 cinghiali, dai quali ne sono stati uccisi 5.

 

 

Non esistono altri eventi possibili oltre a quelli stimati; di conseguenza, la somma delle loro probabilità è uguale a 1(o 100%).

La rappresentazione grafica delle probabilità mostra l’effetto del diverso rapporto tra maschi e femmine nel campione, per cui la distribuzione non è simmetrica

 

 

Figura 8.  Probabilità di uccidere r femmine (da 0 a 3) sui 9 cinghiali.

 

La distribuzione ipergeometrica è definita da 3 parametri (N, n₁ ed n, che rappresentano nell’ordine il numero totale di individui che formano la popolazione, il numero degli oggetti del gruppo considerato, il numero di individui estratti) in funzione del quarto (r, il numero di individui estratti appartenenti al gruppo considerato).

Per N che tende all'infinito, la distribuzione ipergeometrica converge verso la distribuzione binomiale, poiché le probabilità restano praticamente costanti. Di conseguenza, la ipergeometrica è una distribuzione tipica di eventi che riguardano i gruppi formati da poche unità.

 

Nella distribuzione ipergeometrica,

- la media m è  ;  poiché,

 essa risulta uguale a n×p e quindi alla media della distribuzione binomiale corrispondente.

 

La varianza s² è uguale a

;

pertanto, (poiché è minore di 1)

è inferiore alla varianza della binomiale, per gli stessi valori di N e di p.

 

 

2.3.6   DISTRIBUZIONE BINOMIALE NEGATIVA

Tra le distribuzioni teoriche discrete, nella ricerca ambientale e biologica una delle più importanti è la distribuzione binomiale negativa. Ha forse un numero maggiore di applicazioni delle precedenti; ma è più complessa, sia per gli aspetti teorici e matematici, sia nei calcoli.

Come quella binomiale e quella poissoniana, la distribuzione binomiale negativa permette la stima delle probabilità di eventi,  misurati mediante un conteggio.

In botanica e in ecologia, permette l’analisi della distribuzione territoriale di popolazioni animali e vegetali; in epidemiologia, l'analisi del numero di ammalati in periodi brevi di tempo e in popolazioni piccole, in intervalli abbastanza luoghi; nell’industria, quella del numero scarti o di errori nella produzione varia nel tempo o tra macchine e operatori. In generale, serve quando si elenca il numero di eventi avvenuti per unità temporali o spaziali. Ad esempio, con una rilevazione di 200 giorni su un lungo tratto stradale, può essere il conteggio di incidenti avvenuti ogni giorno; oppure, su 200 km di percorso, il conteggio di quelli avvenuti in un decennio, per ogni tratto lungo un Km. 

 

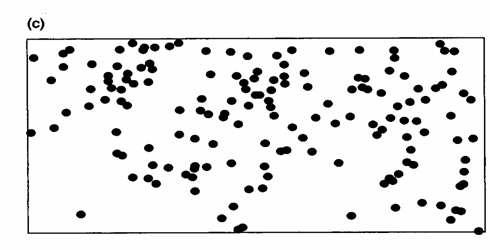
Figura 9. Tipi principali di aggregazione:

a) gruppi piccoli

b)  gruppi larghi, con altri individui distribuiti a caso

c)  gruppi larghi, con altri individui distribuiti in modo regolare

 

La distribuzione tende a essere binomiale negativa quando, come molto spesso succede,

- quando la distribuzione degli eventi è aggregata, vale a dire le probabilità cambiano. Nell’esempio dell’autostrada, si ha una distrbzuione binomiale negativa quando il numero di incidenti cambia perché sono diverse le condizioni meteorologiche oppure perché non tutti i tratti del percorso hanno la stessa pericolosità.

 

In modo didattico, l’infinita varietà di forme della distribuzione geografica di gruppi di individui è schematizzata in tre tipi principali, riportati graficamente nella figura precedente:

 a – gruppi piccoli,

 b – gruppi larghi, con altri individui distribuiti in modo random,

 c – gruppi larghi, con altri individui distribuiti in modo regolare.

 

Per  grande e probabilità  basse, quando la media  è piccola, unica o costante per tutta l’area o per tutto il periodo presi in considerazione, le frequenze attese sono fornite dalla distribuzione poissoniana. Come già illustrato, in essa la varianza   e la media  sono uguali:

Ma quando il fenomeno è complesso e la distribuzione di frequenza è determinata da due o più fattori, ognuno con una media  diversa ma sempre piccola, si ha la distribuzione binomiale negativa. Può essere vista come una mistura o combinazione di altre distribuzioni. Spesso è sinonimo di distribuzioni aggregate.

In essa, la varianza  è superiore alla  media :

 

Nella presentazione delle distribuzioni precedenti, è stato evidenziato che

dove  indica la probabilità del successo e  la probabilità dell'evento alternativo.

Le differenze fondamentali tra la distribuzione binomiale, poissoniana e binomiale negativa sono collegate ai loro diversi rapporti tra media e varianza.

Con  prove,

-  la distribuzione binomiale è caratterizzata da una varianza  inferiore alla media (), dato che ;

-  la distribuzione poissoniana ha una varianza uguale alla media () poiché ;

-  la distribuzione binomiale negativa è caratterizzata da una varianza superiore alla media (); quindi dovrebbe avere  

 

Per introdurre i concetti sui quali è fondata la distribuzione binomiale negativa, è possibile partire da una considerazione ovvia: quando si analizza la distribuzione territoriale di un gruppo di animali o di una specie vegetale, i dati sperimentali evidenziano spesso, come dato di fatto, che

-  la varianza () è superiore alla media ().

Da questa semplice osservazione, si deducono alcune contraddizioni logiche:

a)  poiché , deve essere necessariamente ; quindi  (uguale a ) ha un valore negativo; ma  rappresenta la probabilità che avvenga un evento e quindi non può essere negativa;

b)  inoltre, poiché la media () deve essere positiva (in quanto media di eventi), con  negativo, anche  deve essere negativo; ma  è un conteggio e quindi al massimo può essere nullo, mai negativo. 

 

E’ una serie di illogicità che complica la soluzione matematica della distribuzione binomiale negativa.

Le soluzioni proposte sono numerose.

In una di esse, si pone , con  intero positivo.

Quindi con  (che è mantenuto inalterato)

 il binomio assume la forma

 

da cui il nome di binomiale negativa (l’esponente  è chiamato negative-binomial ).

 

Usando una scala continua, quindi con valori indicati con X, il termine generale per la distribuzione binomiale negativa è

 dove

- P = probabilità di un quadrato di contenere X individui o di una unità di tempo di avere X casi

- x = il conteggio delle unità di venti (0, 1, 2, 3, …)

- m = media della distribuzione per unità di superficie o di tempo

- k = esponente binomiale-negativo

-  G = funzione Gamma.

 

Come evidenzia la figura successiva,

la distribuzione binomiale negativa è unimodale e ha forma simile alla distribuzione di Poisson, ma con frequenze maggiori agli estremi e minori nella parte centrale.

 

 

Figura 9.  Distribuzione binomiale negativa ()

 

 

La funzione Gamma può essere bene approssimata dalla formula di Stirling

 

 

(la virgola e il punto sono usati con simbologia italiana).

I parametri essenziali, poiché gli altri possono essere derivati matematicamente da questi come precedentemente dimostrato, sono 2:

  la media  e l'esponente , da cui

La varianza teorica o attesa  della binomiale negativa è

 da cui si deduce che sempre .

Con dati sperimentali, al posto di m si usa  e, sviluppando la formula generale precedente,

-  la probabilità P di osservare 0 individui per quadrato è

 

 

- la probabilità P di osservare 1 individuo per quadrato è

 

 

- la probabilità P di osservare 2 individui per quadrato è

 

 

- la probabilità P di osservare 3 individui per quadrato è

 

 

- la probabilità P di osservare 4 individui per quadrato è

 

 

L’esponente k è il parametro più difficile da stimare dipendendo, con, sia da m sia da .

Inserendo la varianza campionaria () al posto di quella della popolazione ()

nella relazione

 una prima stima approssimata di  è 

 

Per il calcolo della distribuzione teorica a partire da dati campionari, sono stati proposti vari metodi, che dipendono

-  sia dalle dimensioni del campione (ad esempio, in un conteggio su una superficie divisa in tanti quadrati uguali, da  =  numero di quadrati),

-  sia dal numero di individui per unità di rilevazione (vale a dire dalla media  e dalla varianza  degli individui presenti nell’insieme dei quadrati).

Il testo di Charles J. Krebs del 1999 Ecological Methodology (2^nd ed. Benjamin/ Cummings, Addison Wesley Longman, Menlo Park , California, p. X + 620) propone alcuni metodi approssimati, per risolvere il problema. Per ulteriori approfondimenti di questa metodologia e lo sviluppo di esempi, si rinvia ad esso.

 

Per calcolare una distribuzione teorica binomiale negativa a partire da una distribuzione osservata, esistono altre proposte.

La stima fornita dal metodo del maximum likelohood (maximum likelihood estimation) non porta a formule semplici, in questo caso.

Una delle soluzioni operativamente più semplici è fornita da Owen L. Davies e Peter L. Goldsmith nel testo del 1980 Statistical Methods in Research and Production with special regference the Chemical Industry (4^th revised ed. Longman Group Limited, London, XIII + 478 p.). Per risolvere il problema delle contraddittorietà generate dal fatto che

-  la varianza () è superiore alla media (),

- la media e la varianza sono date in termini di  e

 

 

 da cui si ricava

 

Con una distribuzione campionaria, i parametri  e  sono stimati rispettivamente

-  a partire dalla media  e dalla varianza  osservate.

 

Da esse si ricavano

-    e   con

     e    

 

- e  le proporzioni   e   con

 

     e    

 

Infine le probabilità che i diversi eventi avvengano 0, 1, 2, 3, 4,ecc., volte

 sono determinate mediante lo sviluppo di

 

 che è appunto una binomiale con un indice negativo.

 

Nella pratica, per il calcolo della probabilità che l’evento succeda 0 volte, 1 volta, 2, 3 , 4, ecc.  volte,

-  la parte  resta costante, una volta stimate   e   ,

-  mentre la parte , una volta stimate   e    diventa:

 

 

 

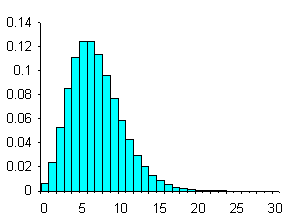
ESEMPIO. Su un tratto auto stradale di 269 Km, è stato contato il numero di tamponamenti avvenuti in cinque anni, per ogni tratto della lunghezza di un Km. Il conteggio del numero di eventi ha dato il risultato seguente

 

 

 

 

Calcolare la distribuzione binomiale negativa e quella possoniana equivalenti.

Alla fine, trarre le conclusioni dal loro confronto con la distribuzione osservata.

 

Risposta.

A- Per la distribuzione binomiale negativa,

1 -  dapprima occorre calcolare la media delle  classi:  

 

Con la  distribuzione osservata, si ottiene che

 

 

(* Nella classe  è stimato che siano presenti un 9 e un 10, con totale 19 e valore medio  = 9,5)

 

-   il numero di tratti o Km considerati è 269,

-   il numero totale di tamponanti è 537

-   la media per Km risulta  = 1,996

 

2 –  Dalla distribuzione dei dati per classe e dalla media, si ricava

 la varianza

 

Con la  distribuzione campionaria

 

 

 

 

 si ottiene  = 2,735

 

 3 – Da  = 1,996  e    = 2,735  si derivano i parametri , , ,

 della distribuzione binomiale negativa

 

 

 

 

 

 ricavando      = 2,701         = 5,391         = 0,730        .

 

4 – Con esse, si possono ricavare le frequenze attese

-  Per , la probabilità è  = 0,1833

 

-  Per , la probabilità è = 0,2668

 

-  Per , la probabilità è = 0,2301

 

-  Per , la probabilità è = 0,1533

 

-  Per , la probabilità è = 0,0865

 

-  Per , la probabilità è = 0,0460

 

-  Per , la probabilità è = 0,0212

 

Per la difficoltà pratica di continuare il calcolo con una semplice calcolatrice manuale e per l’approssimazione delle stime a causa degli arrotondamenti, è conveniente stimare la probabilità di avere 7 o più eventi, cumulando le probabilità più estreme.

In modo molto semplice può essere ottenuto per sottrazione da 1 delle probabilità già stimate per gli altri eventi:

0,1833 + 0,2668 + 0,2301 + 0,1533 + 0,0865 + 0,0460 + 0,0212 = 0,9872

-  Per , la probabilità è =  1 – 0,9872 = 0,00128

 

In conclusione, le probabilità determinate con la distribuzione binomiale negativa sono

 

 

 

 B - Per la distribuzione poissoniana,

 si utilizza la formula

 

 nella quale l’unico parametro che occorre calcolare dalla distribuzione osservata è la media.

Resa più semplice per i calcoli, con = 2,71828 e con  = 1,996 può essere scritta

 come

 

-  Per  = 0, la probabilità è  = 0,1359

 

-  Per  = 1, la probabilità è = 0,2713

 

-  Per  = 2, la probabilità è = 0,2707

 

-  Per  = 3, la probabilità è = 0,1801

 

-  Per  = 4, la probabilità è = 0,0899

 

-  Per  = 5, la probabilità è = 0,0359

 

-  Per  = 6, la probabilità è = 0,0119

 

Per  la probabilità può essere ottenuta per sottrazione da 1 delle probabilità già stimate per gli altri eventi:

0,1359 + 0,2713 + 0,2707 + 0,1801 + 0,0899 + 0,0359 + 0,0119 = 0,9957

-  Per , la probabilità è =  1 – 0,9957 = 0,0043

 

In conclusione, le probabilità determinate con la distribuzione Poissoniana sono

 

 

 

Per un confronto tra la distribuzione osservata e le due distribuzioni teoriche calcolate, è utile una tabella riassuntiva

 

 

dove

-  la probabilità  osservata è calcolata da

-  la probabilità  osservata è calcolata da , ecc.

-  la probabilità  osservata e stimata da , ecc.

 

Dal semplice confronto visivo, risulta con evidenza la maggiore affinità della distribuzione osservata con la distribuzione binomiale negativa. La distribuzione poissoniana ha valori più bassi agli estremi e più alti nelle classi centrali, vicini alla media  = 1,996

 

Ma per valutare il grado di accordo tra la distribuzione osservata e una delle due distribuzioni teoriche, è necessario ricorre a test sulla bontà dell'adattamento (goodness of fit test), quali il test , il test G² e il test di Kolmogorov-Smirnov, che sono illustrati nei capitoli successivi.

 

Per questi test, si devono utilizzare le frequenze assolute, non quelle relative.

Il numero totale di osservazioni effettuate è un parametro molto importante per la significatività di questi test. Con le stesse frequenze relative, la significatività dei test risulta tanto maggiore quanto più numeroso è il campione.

Rapportati al totale di 269 casi analizzati, la distribuzione del numero di eventi è

 

 

 

Ovviamente l'interpretazione visiva di quale delle sue distribuzioni teoriche sia in maggiore accordo con quella sperimentale non varia, rispetto alla descrizione effettuata con le proporzioni.

Anche in questo settore di applicazione della statica, è sempre importante passare dalla interpretazione statistica a quella disciplinare. E' questa la vera competenza richiesta nella  statistica applicata: saper coniugare una buona preparazione statistica con la corretta e approfondita conoscenza dei problemi ai quali viene applicata.

 

L'interpretazione disciplinare dell'accordo tra la distribuzione osservata e quella binomiale è che nel fenomeno analizzato esiste non una media sola, ma sono presenti più medie.

Esse sono tra loro tanto più differenti, quanto maggiore è la varianza calcolata sul campione rilevato.

Riportata ai 269 Km analizzati, questa interpretazione significa che in certi tratti autostradali la frequenza media di incidenti è bassa, mentre in altri è sensibilmente più alta. Sotto l'aspetto operativo, per ridurre il numero di incidenti, è conveniente intervenire dove la pericolosità del tracciato è maggiore. Invece, se l'accordo maggiore fosse stato tra la distribuzione osservata e quella poissoniana, si sarebbe dovuto concludere che la probabilità di incidenti è costante su tutto il percorso. La conseguenza pratica sarebbe stata che una riduzione del numero di incidenti avrebbe potuto essere ottenuta solamente con misure generali, quali i limiti inferiori di velocità, estesi a tutto il tracciato.

Nell'industria, se il numero di scarti per giorno oppure per lotto segue una distribuzione poissoniana, significa che  la probabilità di errori è casuale e costante; una riduzione degli scarti è ottenuta solo con un miglioramento delle macchine o un aggiornamento esteso a tutti gli addetti. Se invece segue una distribuzione binomiale negativa, significa che non tutte le macchine sono uguali e/o gli operatori non hanno tutti le stesse capacità; è conveniente intervenire su queste cause specifiche e non con provvedimenti generali.

 

2.3.7   DISTRIBUZIONE UNIFORME O RETTANGOLARE

La più semplice distribuzione discreta è quella uniforme; la sua caratteristica fondamentale è l'identica possibilità del verificarsi di tutti i risultati possibili. Per esempio, la probabilità che esca un numero da 1 a 6 con il lancio di un dado non truccato è uguale per ognuno dei 6 possibili risultati.

Ad essa si ricorre con frequenza quando, in assenza di ipotesi specifiche più dettagliate o di una conoscenza precisa del fenomeno, la verifica di una distribuzione uniforme rappresenta un punto di partenza minimo, che è quasi sempre accettabile.

L'espressione matematica con cui calcolare la probabilità che una variabile discreta X, che segue la distribuzione uniforme, assuma un particolare valore è stabilita da

 

 dove:

-    = risultato maggiore  possibile di X

-    = risultato minore possibile di X.

 

Nell'esempio dei dadi, è semplice verificare che con b = 6   e   a = 1

 si ottiene una probabilità

 pari a 1/6.

 

Nella distribuzione discreta uniforme la media è

 

 e la deviazione standard s  è

 

La utilizzazione della distribuzione rettangolare è limitata quasi esclusivamente all'analisi di probabilità a priori. Un caso che ricorre con frequenza nella ricerca ambientale è l’analisi della frequenza di animali in varie aree, per verificare un’omogeneità di dispersione. L’ipotesi alternativa è l’esistenza di una associazione tra presenza (o assenza) della specie e la condizione ambientale dell’area.