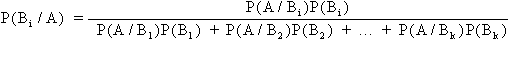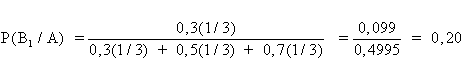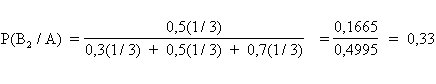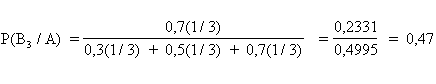DISTRIBUZIONI  e  leggi  di  probabilità'

 

 

2.2. DEFINIZIONI DI PROBABILITA’: MATEMATICA, FREQUENTISTA E SOGGETTIVA, CON ELEMENTI DI STATISTICA BAYESIANA

 

 

In un gioco fondato su eventi casuali, mutuamente esclusivi, ugualmente possibili ed indipendenti, il risultato di ogni singolo tentativo è imprevedibile. Ma su un elevato numero di tentativi, si stabiliscono regolarità e leggi. A lungo termine, l'esito è prevedibile. Le probabilità dei successi e quelle d’ogni evento alternativo possono essere calcolate con precisione crescente all'aumentare del numero di osservazioni.

La natura del concetto di probabilità è chiarita dal teorema di Bernoulli. Prende il nome da Jacques Bernoulli (1654-1705), matematico svizzero, per quanto egli ha scritto nel suo libro Ars Conjectandi, pubblicato postumo nel 1713.

Questo teorema è chiamato anche legge dei grandi numeri e meno frequentemente convergenza in probabilità.

Può essere enunciato in questo modo:

- un evento, che abbia probabilità costanti P, in una serie di prove tende a P, al crescere del numero di tentativi.

 

Il concetto di probabilità classica, fondato su una probabilità matematica o a priori, è stato il primo ad essere definito. E' la probabilità di ottenere testa o croce con una moneta, di avere un numero da 1 a 6 con un dado o in più lanci, di prevedere i possibili ordini d'arrivo in una gara con diversi concorrenti che rispettino le 4 condizioni citate. Non si richiede nessun dato sperimentale; i risultati sono conosciuti a priori, senza attendere alcuna rilevazione od osservazione, poiché è sufficiente il solo ragionamento logico per calcolare con precisione le probabilità. Se la moneta, il dado e la gara non sono truccate, le verifiche sperimentali si allontaneranno dai dati attesi solo per quantità trascurabili, determinate da eventi casuali o da errori di misura.

Queste probabilità non sono determinate solamente da leggi matematiche. Una volta compresi i meccanismi della natura, molte discipline evidenziano regolarità, sovente chiamate leggi, che permettono di stimare in anticipo e con rilevante precisione i risultati di esperimenti od osservazioni. In biologia è il caso sia delle leggi di Mendel, che permettono di calcolare le frequenze genotipiche e fenotipiche attese nell'incrocio tra ibridi, sia della legge di Hardy-Weinberg, utile per definire le frequenze genetiche in una popolazione mendeliana panmittica.

Fermo restando il numero di casi possibili, la probabilità di un evento aumenta quando cresce il numero dei casi favorevoli; oppure quando, fermo restando il numero di casi favorevoli, diminuisce quello dei casi possibili.

La definizione di probabilità classica è attribuita sia a Bernouilli, sia a Laplace (il francese Pierre-Simon, marchese di Laplace, nato nel 1749 e morto nel 1827, le cui opere più importanti sono Traité de Mécanique Céleste in cinque volumi e il volume  Théorie Analytique des Probabilité):

-  la probabilità di un evento casuale è il rapporto tra il numero di casi favorevoli ed il numero di casi possibili, purché siano tutti equiprobabili.

 

La stima di una probabilità a priori ha limitazioni gravi nella ricerca sperimentale: per calcolare la probabilità di un evento, è necessario conoscere preventivamente le diverse probabilità di tutti gli eventi possibili. Pertanto, questo approccio non può essere utilizzato sempre. Con la probabilità matematica non è assolutamente possibile rispondere a quesiti che per loro natura richiedono un approccio empirico, che possono essere fondati solo su osservazioni sperimentali ripetute, poiché i diversi risultati ottenibili non sono tutti ugualmente possibili, né casuali. Per esempio, come rispondere alla domanda: “Con un dado truccato, quali sono le probabilità che esca il numero 5?”. Occorre fare esperimenti con lanci ripetuti, per sapere come quel dado è truccato e quindi quali siano le effettive probabilità di ogni numero.

 

Nello stesso modo, se nella segregazione di un diibrido o nella distribuzione di un carattere ereditario intervengono fenomeni di selezione, con un’intensità ignota, quali saranno le probabilità dei vari fenotipi di essere presenti in una data generazione?  Ogni alterazione dei rapporti di equiprobabilità o dei fenomeni di casualità, i soli che possano essere stimati a priori sulla base della logica, richiede l’esperienza di almeno una serie di osservazioni ripetute.

 

Come stima della probabilità di un evento sperimentale può essere utilizzata la sua frequenza, quando essa nelle varie ripetizioni si mantiene approssimativamente costante. Una definizione chiara di questo concetto è stata data nel 1920 dal matematico von Mises (Richard Martin Edler von Mises, nato in Russia nel 1883 e morto in America nel 1953, dopo aver insegnato matematica applicata a Berlino e a Istanbul).

Egli scrive:

-  la probabilità di un evento casuale è il limite a cui essa tende al crescere del numero delle osservazioni, in una serie di esperienze ripetute nelle stesse condizioni.

 

Se F è la frequenza relativa di un evento in una popolazione, generalmente si può osservare che, all’aumentare del numero di osservazioni (n), la frequenza (f) del campione tende a diventare sempre più simile a quella reale o della popolazione (F). Questa affermazione non può essere dimostrata né con gli strumenti della matematica, in quanto si riferisce a dati osservazionali, né in modo empirico, poiché nella realtà un esperimento non può essere ripetuto infinite volte. Tuttavia è una regolarità statistica, chiamata legge empirica del caso, che costituisce la base sperimentale sia di ogni teoria statistica sia del ragionamento matematico.

In questi casi, si parla di probabilità frequentista o frequentistica, di probabilità a posteriori, di legge empirica del caso o di probabilità statistica.

Essa può essere applicata in tutti i casi in cui le leggi dei fenomeni studiati non sono note a priori, ma possono essere determinate solo a posteriori, sulla base dell'osservazione e delle misure statistiche. Per calcolare la probabilità di trovare un numero prestabilito di individui di una certa specie in una popolazione formata da specie diverse, deve essere nota una legge o regola della sua presenza percentuale, che può essere stabilita solamente con una serie di rilevazioni. Per stimare la probabilità di trovare un individuo oltre una cerca dimensione, è necessario disporre di una distribuzione sperimentale delle misure presenti in quella popolazione.

Solamente in un modo è possibile rispondere a molti quesiti empirici: concepire una serie di osservazioni od esperimenti, in condizioni uniformi o controllate statisticamente, per rilevarne la frequenza.

 

I due tipi di probabilità presentati, quella classica e quella frequentista, hanno una caratteristica fondamentale in comune: entrambe richiedono che i vari eventi possano essere ripetuti e verificati in condizioni uniformi o approssimativamente tali. In altri termini, si richiede che quanto avvenuto nel passato possa ripetersi in futuro. Ma esistono anche fenomeni che non possono assolutamente essere ridotti a queste condizioni generali, perché considerati eventi unici od irripetibili. Per esempio, come è possibile rispondere alle domande: “Quale è la probabilità che avvenga una catastrofe o che entro la fine dell'anno scoppi la terza guerra mondiale? Quale è la probabilità che una specie animale o vegetale a rischio effettivamente scompaia? Quale è la probabilità che un lago, osservato per la prima volta, sia effettivamente inquinato?”.

 

E’ il caso del medico che deve stabilire se il paziente che sta visitando è ammalato; di una giuria che deve emettere un giudizio di colpevolezza o di assoluzione; di tutti coloro che devono decidere in tante situazioni uniche, diverse ed irripetibili.

Sono situazioni che presuppongono

-  il giudizio di numerosi individui sullo stesso fenomeno oppure la stima personale di un solo individuo sulla base di un suo pregiudizio o della sua esperienza pregressa.

Il valore di probabilità iniziale non è fondato né sulla logica matematica né su una serie di esperimenti.

Nella teoria della probabilità si sono voluti comprendere anche questi fenomeni non ripetibili. Da questa scelta, deriva un’altra concezione della probabilità: quella soggettiva o personalistica.

 

L'obiezione fondamentale a questa probabilità logica è come misurare un grado di aspettativa, quando è noto che individui diversi attribuiscono probabilità differenti allo stesso fenomeno. E' una critica che viene superata dall'approccio soggettivo, secondo il quale

-  la probabilità è una stima del grado di aspettativa di un evento, secondo l'esperienza personale di un individuo.

 

La probabilità nell'impostazione soggettivista, detta anche "bayesiana", viene intesa come una misura della convinzione circa l'esito di una prova o che accada un certo evento. E’ un approccio che ha vaste ed interessanti applicazioni nelle scienze sociali ed in quelle economiche, dove la sola attesa di un fenomeno o la convinzione di una persona influente sono in grado di incidere sui fenomeni reali, come la svalutazione, i prezzi di mercato, i comportamenti sociali. In medicina, è il caso della decisione sulla cura da prescrivere al paziente.

Per la statistica, il problema fondamentale consiste nell'indicare come si debba modificare la probabilità soggettiva di partenza, in dipendenza dei successivi avvenimenti oggettivi, quando non si dispone di repliche. Per coloro che ritengono che il mondo esterno sia una realtà oggettiva, conoscibile ed indipendente da loro, la conoscenza obiettiva non può derivare da convinzioni personali o da preferenze individuali; pertanto, l'approccio soggettivo non sarebbe attendibile, in quanto non permetterebbe la conoscenza oggettiva del reale.

Questa varietà e contrapposizione di concetti, sinteticamente esposti in modo elementare, sul significato più esteso e comprensivo di probabilità, si riflettono sulla interpretazione delle stime ottenute da dati sperimentali; ma gli aspetti formali del calcolo variano solo marginalmente. Nel contesto delle scienze sperimentali, esistono casi di applicazione della probabilità soggettiva; in particolare, quando si tratta di scegliere una strategia o prendere una decisione.

 

Nella ricerca biologica, ecologica ed ambientale, di norma predominano i casi in cui si studiano eventi ripetibili, in condizioni almeno approssimativamente uguali o simili. Pertanto, quasi esclusivamente si fa ricorso all'impostazione frequentista della probabilità, trascurando l'impostazione soggettivistica.

Il teorema di Bayes (1702-1761) pubblicato nel 1763 (nel volume Essay Towards Solving a Problem in the Doctrine of Chance), due anni dopo la morte dell'autore (il reverendo Thomas Bayes), si fonda su probabilità soggettive. Spesso è presentato come alternativo alla inferenza statistica classica, detta anche empirica.

Più recentemente, sono stati sviluppati metodi quantitativi che incorporano l'informazione raccolta anche con dati campionari. E' quindi possibile correggere la stima di una probabilità soggettiva originaria, detta probabilità a priori, mediante l'informazione fornita da successive rilevazioni campionarie, per ottenere una probabilità a posteriori.

 

Ad esempio, si consideri un evento A la cui probabilità a priori, soggettiva perché espressione di convinzioni e sovente determinata da carenza di informazioni, sia P(A). Dall'esperienza (analisi di un campione) si rileva la probabilità P (intesa, in questo caso, in senso frequentista od empirico) di un certo evento B. Ci si chiede in quale modo la realizzazione dell'evento B modifichi la probabilità a priori di A, cioè qual è il valore di P(A/B) (la probabilità dell’evento A condizionato B).

(Ricordiamo che l'espressione P(A/B) indica la probabilità condizionale di A rispetto a B, cioè la probabilità dell'evento A stimata sotto la condizione che si sia realizzato l'evento B).

 

Per il teorema delle probabilità composte, applicato ad eventi non indipendenti, la probabilità che gli eventi A e B si verifichino contemporaneamente è data da

                                                                                                         (1a)

ed inversamente anche da

                                                                                                         (1b)

Da queste due equazioni si ottiene

                                                                                          (2)

e, dividendo per P(A), si perviene

                                                                                                           (3)

 alla formula generale.

Da essa è possibile dedurre che, per k eventi reciprocamente incompatibili e collettivamente esaustivi, dove B₁, B₂, ..., B₃  sono gli eventi mutuamente esclusivi, si ottiene il Teorema di Bayes

 

          (4)

dove

-          P(B_i) è la probabilità a priori che è attribuita alla popolazione B_i prima che siano conosciuti i dati,

-           P(A/B_i) rappresenta la probabilità aggiuntiva dopo che è stata misurata la probabilità di A.

 

Con un esempio, è possibile presentare in modo elementare la successione logica delle stime di probabilità.

1) Si supponga di disporre di un campione A di individui della specie Y e di chiedersi da quale delle tre località indicate (B₁, B₂, B₃) esso possa provenire.

La stima iniziale o probabilità a priori, necessaria quando non si possiede alcuna informazione, è fondata sul caso oppure su distribuzioni teoriche. In questa situazione di totale ignoranza iniziale della possibile provenienza degli individui della specie Y, la scelta più logica può essere quella di attribuire ad ognuna delle 3 località le medesime probabilità P; è una distribuzione non informativa che può essere scritta come:

P(B₁) = P(B₂) = P(B₃) = 1/3

 

2) Come secondo passaggio, si supponga ora che un’analisi abbia rivelato che nelle tre diverse località (B₁, B₂, B₃) che possono esserne il luogo d'origine, questa specie sia presente con frequenze percentuali differenti, in comunità delle stesse dimensioni:

-          nella prima, che indichiamo con B₁, ha una presenza del 30%

-          nella seconda, indicata con B₂, una presenza del 50%

-          nella terza, indicata con B₃, il 70%.

 

Dopo questa informazione che può essere scritta come

P(A/B₁) = 0,3          P(A/B₂) = 0,5       P(A/B₃) = 0,7

il calcolo delle probabilità a posteriori, da attribuire ad ogni comunità, può essere attuato mediante il teorema di Bayes.

Da esso mediante i rapporti

 

 

 si ricava che il campione A di individui della specie Y ha

-          una probabilità del 20% di provenire dalla località B₁,

-          una probabilità pari al 33% di essere originario della località B₂,

-           una del 47% di provenire dalla B₃.

Ovviamente i 3 eventi sono reciprocamente incompatibili e collettivamente esaustivi, per cui la somma delle probabilità è unitaria, se espressa in rapporti, o pari al 100%, se espressa in percentuale.

 

3) Con una ulteriore raccolta di dati (sia soggettivi che sperimentali o frequentisti), è possibile calcolare una nuova distribuzione delle probabilità a posteriori, per inglobare le nuove informazioni ed aggiornare la stima.

Se nel conteggio del campione A, si osserva che sono presenti 10 individui di cui 8 della specie Y, come variano le probabilità che il campione A derivi rispettivamente dalla località B₁, dalla B₂ o dalla B₃?

In questa terza fase, il primo passo logico è calcolare la probabilità di trovare la distribuzione osservata nel campione (8 individui della specie Y su 10 complessivi), se fosse stato estratto casualmente da ognuna delle 3 comunità:

a - dalla comunità B₁ dove la specie Y ha una proporzione uguale a 0,3

b - dalla comunità B₂  dove la specie Y ha una proporzione uguale a 0,5 

c - dalla comunità B₃  dove la specie Y ha una proporzione uguale a 0,7.

 

Per rispondere a tale quesito, si ricorre alla distribuzione binomiale (che sarà spiegata successivamente), della quale sono riportati i risultati.

a)  Nel caso della comunità B₁ dove la proporzione p di individui della specie Y è 0,3

la probabilità P che su 10 individui estratti a caso 8 siano della specie Y è uguale a  0,00145.

 

b) - Nel caso della comunità B₂ dove la proporzione p di individui della specie Y è 0,5

la probabilità P che su 10 individui estratti a caso 8 siano della specie Y è uguale a  0,04394.

 

3 - Nel caso della comunità B₃ dove la proporzione p di individui della specie Y è 0,7

la probabilità P che su 10 individui estratti a caso 8 siano della specie Y è uguale a 0,23347.

 

Le 3 probabilità a posteriori calcolate precedentemente (0,20; 0,33; 0,47) diventano le nuove probabilità a priori. Esse devono essere moltiplicate per le probabilità empiriche fornite dalla nuova osservazione:

 

 

Sulla base delle ultime informazioni raccolte, la nuova risposta è:

-          la probabilità che il campione A sia originario della comunità B₁ diventa  2 su mille (0,002),

-          la probabilità che provenga dalla comunità B₂ diventa 116 per mille (0,116),

-          la probabilità che sia stato raccolto nella comunità B₃ è 882 su mille (0,882).

Non esistono altre possibilità e la loro somma deve essere uguale a 1 (0,002 + 0,116 + 0,882 = 1,0).

 

L’esempio illustra un aspetto peculiare del procedimento inferenziale bayesiano. Con l’aumento del numero di osservazioni campionarie od empiriche, le probabilità attribuite in modo indifferenziato, o almeno simile (come 1/3 all’inizio) tendono a divergere. Il fenomeno è chiamato progressiva dominanza dell’informazione sulla distribuzione a priori.

Un altro aspetto importante è che, partendo da distribuzioni a priori notevolmente differenti (per esempio, in partenza la distribuzione poteva essere 0,1   0,2   0,7), se nessuna di esse è 0 oppure 1 con gli stessi dati sperimentali successivamente raccolti le probabilità tendono a convergere rapidamente. E’ chiamato il principio della giuria: se nessuno dei giudici è prevenuto, ritenendo l’accusato sicuramente colpevole o sicuramente innocente, dopo un numero relativamente basso di verifiche tutti giungono alle stessa probabilità, per quanto distanti siano in partenza.

 

L'analisi bayesiana può essere utilizzata per sommare in modo progressivo l'effetto di tutte le nuove informazioni. Ogni ulteriore indicazione quantitativa permette di aggiornare nuovamente la distribuzione originale precedente; i dati modificano le probabilità stimate inizialmente in condizioni di incertezza o dedotte da una informazione meno precisa. Le ampie possibilità operative di tale teorema derivano dal fatto che le probabilità possono essere tratte indifferentemente da dati oggettivi o da distribuzioni di opinioni, che mutano nel tempo.

 

Nell'esempio presentato, l'inferenza statistica bayesiana è stata applicata a percentuali o proporzioni. Ma essa può essere estesa a qualsiasi altra caratteristica della popolazione, come la media, la varianza, il coefficiente di regressione, per assegnare probabilità specifiche ad ogni possibile valore di questi parametri.

In questo corso, nei paragrafi successivi saranno illustrate le probabilità matematiche di alcune distribuzioni teoriche.

Il corso è fondato solo sulle probabilità frequentiste o a posteriori.

Per un’inferenza fondata sulle probabilità soggettive, utile a coloro che debbono prendere decisioni in situazioni d’incertezza, si rinvia a testi specifici.