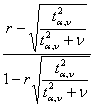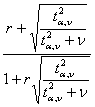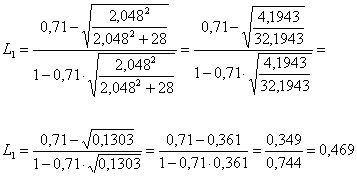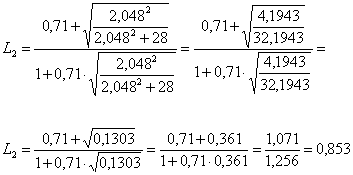CORRELAZIONE  E  COVARIANZA

 

 

18.4.   INTERVALLO DI CONFIDENZA DI r

 

 

Pure nel caso della correlazione, la stima dell’intervallo di confidenza di un parametro richiede che i campioni siano distribuiti in modo simmetrico, rispetto al valore vero o della popolazione. Ma, come giù evidenziato nel paragrafo precedente, a differenza di quanto avviene per la media campionaria  rispetto a m e per il coefficiente angolare b rispetto a b, i valori campionari r

-  sono distribuiti normalmente solo quando

-  il valore di r è piccolo (teoricamente zero)

-  e i campioni sono abbastanza grandi (teoricamente infiniti).

 

Quando il valore di r si allontana da zero, la distribuzione dei valori r campionari è sempre asimmetrica. Di conseguenza, pure conoscendo il valore di r

 e la sua varianza

 oppure il suo errore standard

 

 non è corretto calcolare l’errore fiduciale di r

 attraverso

 applicando alla correlazione

 quanto è possibile per la retta

 

Infatti, a causa dell’asimmetria dei valori campionari attorno alla media quando r ¹ 0

-   i limiti di confidenza, che utilizzano il valore di t e l’errore standard, non sono adatti a verificare la significatività di un qualsiasi valore di correlazione rispetto ad un valore teorico atteso;

-    non è possibile utilizzare il test t per il confronto tra due indici di regressione r₁ e r₂.

 

L’uso di questo test inferenziale è limitato al solo caso in cui si vuole verificare l’assenza di correlazione, espressa dall’ipotesi nulla H₀: r = 0. 

 

Per l’uso generale, con qualsiasi valore di r, dell’intervallo di confidenza, sono stati proposti vari metodi. Ne possono essere citati cinque:

a)   la trasformazione di r in z proposta da Fisher, valida soprattutto per grandi campioni,

b)  il precedente metodo di Fisher, ma con l’uso della distribuzione t di Student al posto della distribuzione normale, più cautelativa per piccoli campioni,

c)   la procedura proposta da M. V. Muddapur nel 1988, che utilizza la distribuzione F (vedi: A simple test for correlation coefficient in a bivariate normal population. Sankyd: Indian J. Statist. Ser. B. 50: 60-68),

d)   la procedura proposta da S Jeyaratnam nel 1992, analoga alla precedente, ma con l’uso della distribuzione t (vedi: Confidence intervals for the correlation coefficient. Statist. Prob. Lett. 15: 389-393).

e)   metodi grafici, come quelli riportati già nel 1938 da F. N. David in Tables of the Correlation Coefficient (ed. E. S. Pearson, London Biometrika Office).

 

 

Il terzo e il quarto metodo, citati anche da J. H. Zar nel suo test del 1999 (Biostatistical Analysis, 4^th ed., Prentice Hall, New Jersey, a pagg. 383-384), offrono il vantaggio di stimare un intervallo generalmente minore di quello di Fisher, oltre all’aspetto pratico di non richiedere trasformazioni di r e quindi di essere più rapidi.

Questi test, come qualsiasi intervallo fiduciale, possono essere utilizzati anche per la verifica dell’ipotesi sulla differenza tra due medie, in un test bilaterale.

 

A) Il metodo di Fisher stima il limite inferiore L₁ e il limite superiore L₂ dell’intervallo di confidenza attraverso le relazioni

L₁ =

L₂ =

 dove

-   è il valore campionario di r trasformato, attraverso

 la relazione

 

-   è il valore della Z nella distribuzione normale alla probabilità a/2, prescelta per definire l’intervallo,

-    è l’errore standard (approssimato)

 di r trasformato in z

 che dipende da n.

 

Successivamente, i due valori stimati L₁ e L₂, calcolati ovviamente in una scala z, devono essere riportati sulla scala di r,

 con la trasformazione

 

In questo ultimo passaggio, si perde la simmetria di L₁ e L₂ rispetto al valore centrale, quando r¹0. L’asimmetria intorno ad r risulta tanto più marcata quanto più esso si avvicina a +1 oppure a -1.

 

B) Più recentemente, in vari testi è proposta la misura più cautelativa, che fornisce un intervallo maggiore in rapporto alla dimensione campionaria n, con la distribuzione t di Student.

Il limite inferiore L₁ e il limite superiore L₂ dell’intervallo di confidenza sono calcolati attraverso le relazioni

L₁ =

L₂ =

 dove

-  è il valore alla probabilità a/2 prescelta per definire l’intervallo, con n = n –2,

 mentre tutti gli altri parametri restano identici a quelli appena presentati.

Nulla cambia rispetto al metodo classico di Fisher, per quanto riguarda

-   dapprima la trasformazione di r in z 

-  successivamente le trasformazioni dei valori L₁ e L₂ in scala r.

 

C) Il metodo proposto da Muddapur, meno noto del metodo classico di Fisher, più recente e più raro in letteratura, ma più rapido in quanto non richiede alcuna trasformazione,

 con L₁

L₁ =

 e L₂

L₁ =

dove

-  F è il valore corrispondente nella distribuzione F di Fisher alla probabilità a per un test bilaterale e con df n₁ = n₂ = n-2

 fornisce una stima uguale a quella classica di Fisher.

 

 

D) Il metodo proposto da Jeyaratnam, che può essere letto come una variante del precedente, una sua formula abbreviata in quanto ancor più rapido

con L₁

L₁ =

 e L₂

L₂ =

dove

-   t è il valore corrispondente nella distribuzione t di Student alla probabilità a per un test bilaterale (come in tutti gli intervalli fiduciali) e con df n = n-2

-   n = n-2.

 

ESEMPIO. Con 30 coppie di dati, è stato calcolato il coefficiente di correlazione lineare semplice r = 0,71.

Entro quale intervallo si colloca il valore reale o della popolazione (r), alla probabilità a = 0.05?

Calcolare i valori estremi L₁ e L₂ dell’intervallo fiduciale con i 4 diversi metodi.

 

Risposta

 

 A) Con il metodo classico di Fisher

1 – dopo aver trasformato r = 0,71 in z

 con

 = 0,8872

 ottenendo z = 0,8872

 

2 – si stima il suo errore standard s_z, ovviamente su scala z, con la formula approssimata

 

 = 0,1924

 ottenendo s_z = 0,1924

 

3 – Successivamente, con Z_a/2 = 1,96 (valore della distribuzione normale standardizzata alla probabilità a = 0.05 bilaterale) si stimano i due limiti dell’intervallo L₁ e L₂:

con

 = 0,5101

 si ottiene L₁ = 0,5101

 e con

 = 1,2643

 si ottiene L₁ = 1,2643

 

4 – Per il confronto di L₁ e L₂ con r = 0,71, è necessario ritrasformare i due valori z ottenuti nei corrispondenti valori in scala r. Ricordando che e = 2,718

 per z = 0,5101 con

 

= 0,470

 

 si ottiene L₁ = 0,470

 e per z = 1,2643 con

 

= 0,852

 

 si ottiene L₂ =  0,852

Con il metodo classico di Fisher, l’intervallo di confidenza di r = 0,71 calcolato su 30 copie di dati è compreso tra  i limiti 0,470 e 0,852 con probabilità a = 0.05.

 

 

B) Utilizzando sempre il metodo di Fisher, ma con la distribuzione t al posto della distribuzione z,

1 – i primi due passaggi sono identici ai punti 1 e 2 precedenti, nei quali si era ottenuto

z = 0,8872       e       s_z = 0,1925

 

2 – Dopo aver scelto il valore di t che, con  a = 0.05 bilaterale  e df  n = 28 è

t_{0.025, 28} = 2,048

3 – si ottiene (sempre in scala z)

 = 0,493

 un valore di L₁ = 0,493

 e

 = 1,2814

un valore di L₂ = 1,2814

 

4 – Infine, come nella fase 4 precedente, si riportano questi due valori z in scala r:

 per z = 0,493 con

 

= 0,457

 

 si ottiene L₁ = 0,457

 e per z = 1,2814 con

 

= 0,857

 

 si ottiene L₂ =  0,857.

Con il metodo di Fisher nel quale sia utilizzata la distribuzione t con df n-2, l’intervallo di confidenza di r = 0,71 calcolato su 30 copie di dati è compreso tra i limiti 0,457 e 0,857 con probabilità a = 0.05.

 

 

C) Con il metodo proposto da Muddapur,

1 - dapprima si trova il valore di F alla probabilità a = 0.05 bilaterale con df n₁ = n₂ = 28; rilevato in una tabella molto più dettagliata di quella riportata nelle dispense esso risulta uguale a 2,13;

 

2 – successivamente si calcolano

 L₁ con

 = 0,469

 ottenendo L₁ = 0,469

 e L₂ con

 = 0,853

 ottenendo L₁ = 0,853

 

 

D) Con il metodo proposto da Jeyaratnam,

1 - dapprima si trova il valore di t alla probabilità a = 0.05 bilaterale con df n = 28; esso risulta uguale a 2,13;

 

2 – successivamente si calcolano

 L₁ con

 

 ottenendo L₁ = 0,469

 e L₂ con

 

 ottenendo L₂ = 0,853

 

Questo calcolo diventa molto più rapido se dapprima, separatamente, si stima la parte sotto radice,

 

 che risulta uguale a 0,361:

 

 

 

 

I risultati dei 4 metodi, con i dati dell’esempio, sono riportati nella tabella sottostante:

 

 

E’ sufficiente il semplice confronto, per verificare la loro corrispondenza. I calcoli sono stati fatti alla quarta cifra decimale per evitare arrotondamenti e meglio porre a confronto i risultati.

 

I motivi della trasformazione e suoi effetti sono illustrati da Fisher. Sempre in  “Metodi statistici ad uso dei ricercatori, Torino 1948, Unione Tipografica Editrice Torinese (UTET), 326 p. traduzione di M Giorda, del testo Statistical Methods for Research Workers di R. A. Fisher 1945, nona ed., a pag. 184 e seguenti sono spiegati i motivi e gli effetti della trasformazione di r in z: ”Per piccoli valori di r, z è quasi uguale a r, ma quando r si avvicina all’unità , z cresce senza limiti. Per valori negativi di r, z è negativo. Il vantaggio di questa trasformazione di r in z sta nella distribuzione di coteste due quantità in campioni scelti a caso.

Lo scostamento (errore standard) di r dipende dal valore effettivo della correlazione r, come è rilevato dalla formula

(dove n è il numero di coppie di dati)

Poiché r è un’incognita, dobbiamo sostituirla con il valore osservato r, il quale, in piccoli campioni, non sarà però una stima molto accurata di r. L’errore tipo (errore standard) di z è di forma più semplice e, cioè, approssimativamente,

 

 ed è praticamente indipendente dal valore della correlazione nella popolazione dalla quale si è tratto il campione.

In secondo luogo, la distribuzione di r non è normale in piccoli campioni e, per correlazioni elevate, essa rimane lontana dalla normale anche nei grandi campioni. La distribuzione di z non è strettamente normale, ma tende rapidamente alla normalità quando il campione è accresciuto, qualunque possa essere il valore della correlazione.

Infine la distribuzione di r cambia rapidamente forma quando cambia r;conseguentemente non si può, con ragionevole speranza di successo, tentare di giustificare (leggi: aggiustare) l’asimmetria della distribuzione. Al contrario, la distribuzione di z essendo quasi costante nella forma, l’accuratezza delle prove (leggi: la significatività del test) può essere migliorata per mezzo di piccole correzioni dello scostamento dalla normalità. Tali correzioni sono, però, troppo piccole per assumere importanza pratica e noi non ce ne cureremo. La semplice assunzione che z è normalmente distribuita sarà in tutti i casi sufficientemente accurata.

 

Questi tre vantaggi della trasformazione di r in z  possono notarsi comparando le prossime due  figure.

 

 

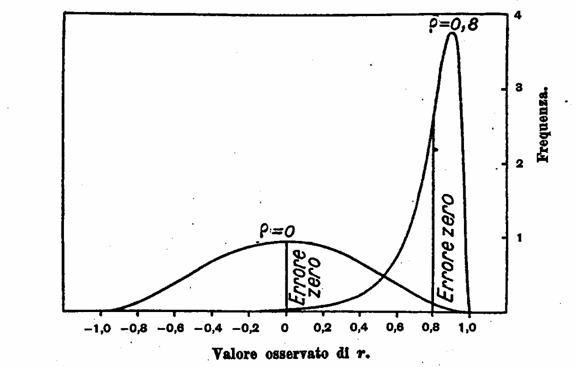
Nella prima sono indicate le distribuzioni effettive di r, per 8 coppie di osservazioni, tratte da popolazioni aventi correlazioni 0 e 0,8:

 

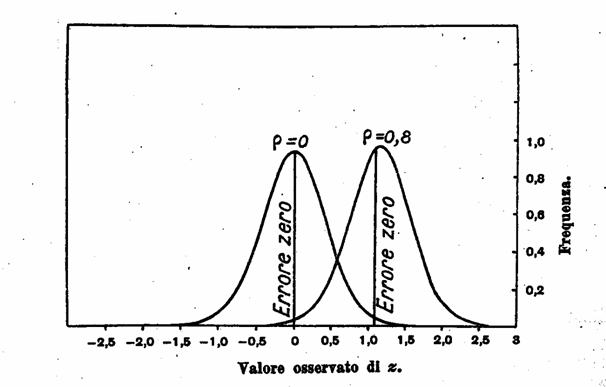
La seconda presenta le corrispondenti curve di distribuzione di z.

 

Le due curve della prima figura sono molto differenti nelle loro altezze modali; entrambe sono nettamente curve non normali; anche nella forma esse sono in forte divario, una essendo simmetrica, l’altra molto asimmetrica.

 

Al contrario, nella seconda figura le due curve non differiscono sensibilmente in altezza; quantunque non esattamente normali nella forma, esse, anche per un piccolo campione di 8 coppie di osservazioni, vi si accostano talmente che l’occhio non può scoprire la differenza; questa normalità approssimativa, infine, eleva agli estremi limiti r = ± 1.

 

Una modalità addizionale è messa in evidenza dalla seconda figura nella distribuzione per r = 0,8. Quantunque la curva stessa, a giudicare dall’apparenza, sia simmetrica, pure l’ordinata dell’errore zero non è posta al centro. Questa figura, infatti, presenta il piccolo difetto che viene introdotto nella stima del coefficiente di correlazione  quale è ordinariamente calcolato.

 

 

 

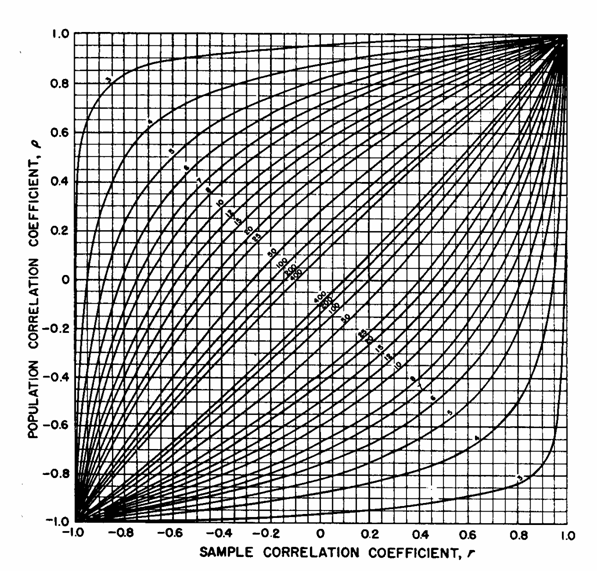
Tra i metodi grafici possono essere ricordati quelli riportati già nel 1938 da F. N. David in Tables of the Correlation Coefficient (ed. E. S. Pearson, London Biometrika Office), almeno per l'importanza della rivista (Biometrika). Essi sono utilizzati anche nel manuale pubblicato dal Dipartimento di Ricerca della Marina Militare Americana nel 1960 (Statistical Manual by Edwin L. Crow, Frances A. Davis, Margaret W. Maxfield, Research Department U. S: Naval Ordnance Test Station, Dover Publications, Inc., New York, XVII + 288 p.).

Come dimostrazione è qui riportato solamente quello per la probabilità a = 0.05. Per le altre si rinvia alle indicazioni bibliografiche riportate.

 

Come in tutti i grafici l'uso è semplice, quasi intuitivo. I limiti consistono soprattutto nell'approssimazione dei valori forniti, determinati dalla lettura su curve molto vicine.

 

 

a = 0.05

Curve degli intervalli di confidenza

per il coefficiente di correlazione r

 

Ad esempio:

- letto, sull'asse delle ascisse, il valore di correlazione r = +0,4 calcolato su un campione di n = 6 dati,

- si sale verticalmente incontrando la curva con il numero 6 due volte:

- la prima in un punto che, proiettato sull'asse delle ordinate, indica r = -0,55

- la seconda in un punto che, proiettato sull'asse delle ordinate, indica r = +0,82.

Sono i due limiti dell'intervallo di confidenza, alla probabilità a = 0.05, per r = 0,4 ottenuto in un campione di n = 6 coppie di osservazioni.

E' importante osservare che essi sono fortemente asimmetrici, intorno al valore campionario calcolato.

La stessa asimmetria esiste se fossimo partiti dal valore vero r  o della popolazione, per stimare la dispersione dei valori campionari r, sempre  calcolati su gruppi di 6 coppie di dati  e alla medesima probabilità di commettere un errore di Tipo I (a = 0.05).