CORRELAZIONE E COVARIANZA

18.18. CONFRONTO TRA QUATTRO OUTPUT INFORMATICI SULLA REGRESSIONE LINEARE SEMPLICE: SAS, MINITAB, SYSTAT, SPSS

Quando si passa dallo studio dalla teoria e dalle formule statistiche alla loro applicazione con dati elaborati mediante programmi informatici, un problema pratico non trascurabile è la capacità di leggere e interpretare i risultati degli output. Nel momento in cui si passa dalle aule ai laboratori, spesso si trovano situazioni differenti da quelle apprese dai libro. E’ un passaggio professionale, ai quali un corso di statistica spesso non prepara, anche quando viene accompagnato da applicazioni al computer.

Al primo approccio, output nuovi presenta difficoltà pratiche, poiché in molti casi:

- sono impostati graficamente in modo dissimile;

- usano termini tecnici differenti, tra loro e da quelli del testo adottato;

- riportano analisi statistiche, che sono diverse, almeno in parte.

Sono situazioni che si presentano anche nel caso più semplice della regressione e della correlazione lineari semplici, dove l’output è limitato a una o al massimo a due pagine.

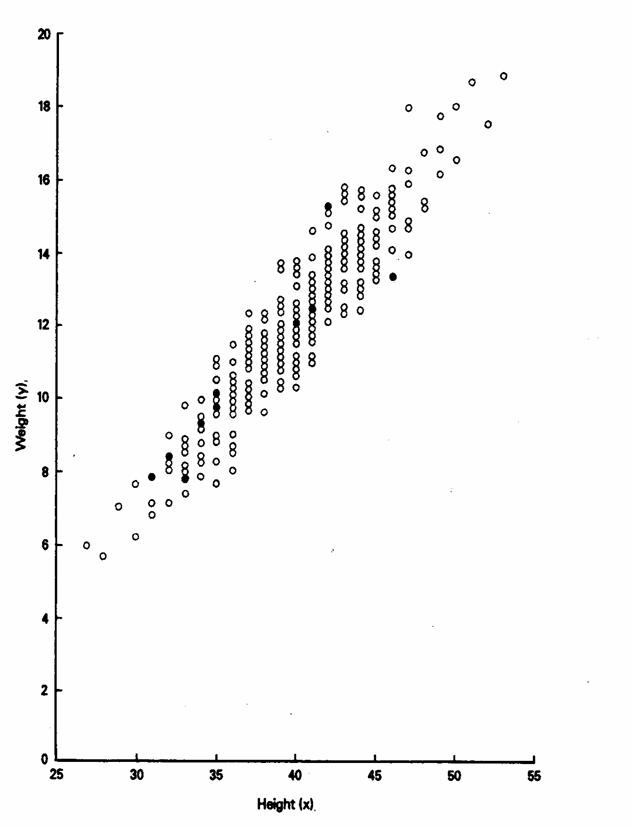
Per preparare a questa situazione, alcuni testi riportano e confrontano gli output di programmi informatici.

Per queste dispense, sono state riprese alcune pagine del volume di Stanton A. Glanz e Bryan K. Slinker del 2001 Primer of applied regression and analysis of variance (2^nd ed. Mc Graw-Hill, Inc., New York, 27 + 949).

Nella diagramma di dispersione successivo, i cerchi rappresentano una popolazione di 200 marziani, dalla quale è stato estratto di un campione di 10 individui, indicati dai cerchi anneriti. Di queste 10 unità campionarie, sono stati misurati l’altezza (sull’asse delle ascisse) e il peso (sull’asse delle ordinate), allo scopo di studiare con le metodologie statistiche le caratteristiche di questi esseri misteriosi.

Nelle due pagine successive sono riportati gli output di quattro programmi statistici a grande diffusione internazionale: SAS, MINITAB, SYSTAT, SPSS, scelti tra i tanti sul mercato, secondo la versione in commercio nell’anno 2000.

E’ evidente la diversa impostazione grafica, nella quale è necessario individuare le informazioni che forniscono i parametri della retta, della correzione e la loro significatività.

Un primo problema da risolvere è il differente numero di cifre decimali per ogni parametro: si va dalle otto del SAS, alle due o tre degli altri programmi. Il numero da riportare nell'articolo o nel rapporto scientifico dipende dalla precisione delle misure introdotte nell’input e dalle dimensioni del campione.

SAS

DEP VAR: W Weight

ANALYSIS OF VARIANCE

SUM OF MEAN

SOURCE DF SQUARES SQUARE F VALUE PROB>F

MODEL 1 44.35755625 44.35755625 47.706 0.0001

ERROR 8 7.43844375 0.92980547

TOTAL 9 51.79600000

ROOT MSE 0.9642642 R-SQUARE 0.8564

DEP MEAN 10.38 ADJ R-SQ 0.8384

C.V. 9.289636

PARAMETER ESTIMATES

PARAMETER STANDARD T FOR H0:

VARIABLE DF ESTIMATE ERROR PARAMETER=0 PROB>

INTERCEP 1 -6.0076 2.39213153 -2.511 0.0363

H 1 0.44410849 0.06429857 6.907 0.0001

MINITAB

The regression equation is

W = -6.008 + 0444 H

Predictor Coef Stdev t-ratio P

Constant -6.008 2.392 -2.51 0.036

H 0.4441 0.06430 6.91 0.000

S = 0.9643 R-sq = 85,6% R-sq(adj) = 83,8%

Analysis of Variance

Source DF SS MS F P

Regression 1 44.358 44.358 47.71 0.000

Error 8 7.438 0.930

Total 9 51.796

SYSTAT

DEP VAR: W N: 10 MULTIPLE R: 0.925 SQUARES MULTIPLE R: 0.856

ADJUSTED SQUARED MULTIPLE R: 0.838 STANDARD ERROR OD ESTIMATE: 0.964

EFFECT COEFFICIENT STD ERROR STD COEF TOLERANCE T P(2 TAIL)

CONSTANT -6.008 2.392 0.000 -2.511 0.036

H 0.444 0.064 0.925 1.000 6.907 0.000

ANALYSIS OF VARIANCE

SOURCE SUM-OF-SQUARES DF MEAN-SQUARE F-RATIO P

REGRESSION 44.358 1 44.358 47.706 0.000

RESIDUAL 7.438 8 0.930

SPSS

Model Summary

Model

R Square

Adjusted

R Square

Std. Error

of the

Estimate

.925^a

.856

.838

.9643

^a Predictor: (Constant), H

ANOVA^b

Model

Sum of

Squares

Mean

Square

Sig.

1 Regression

Residual

Total

44.358

7.438

51.796

44.358

0.930

47.706

.000^a

^a Predictor: (Constant), H

^b Dependent Variable: W

Coefficients^a
Model	Understandardized Coefficients		Standardized Coefficients	T	Sig.
Model	B	Std. Error	Beta	T	Sig.
1 (Constant) H	-6.008 .444	2.392 .064	.925	-2.511 6.907	.036 .000

^a Dependent Variable: W

Con i dati di questo esempio, basterebbe un decimale o al massimo due, data la precisione all’unità con la quale sono state misurate la variabile dipendente e quella indipendente.

Nella lettura dei tabulati è bene seguire un percorso logico, secondo la sequenza:

1 - individuare la variabile dipendente e quella indipendente, con indicazione dei valori della retta di regressione;

2 - valutare la significatività dell’intercetta e del coefficiente angolare, con il test t di Student bilaterale; se l’ipotesi era unilaterale, tale probabilità deve essere dimezzata;

3 - interpretare i risultati del test della linearità, con il test F;

4- e il valore di R-quadro, per un giudizio sulla predittività della retta.

Oltre a

- piccole differenze nelle indicazioni, quali R-SQUARE in SAS, R-sq in MINITAB, come SQUARED MULTIPLE R in SYSTAT e R Square in SPSS,

- e al fatto che il valore della correlazione r = 0,925 sia riportato solamente in SYSTAT dove è indicato con MULTIPLE R e in SPSS dove è indicato con R,

tra i quattro output esistono alcune diversità nel linguaggio:

- l’intercetta è chiamata intercept nel SAS mentre è chiamata constant in MNITAB, SPSS e SYSTAT;

- i coefficienti dell’equazione della regressione sono indicati con coefficient in MINITAB e SYSTAT, mentre sono chiamati parameter estimate in SPSS e B in SPSS;

- la devianza (SS) e la varianza (S) della regressione sono chiamate model nel SAS e regression negli altri tre programmi;

- l’errore standard, vale a dire la radice quadrata della varianza d’errore, è indicata con std. error of the estimate in SPSS e SYSTAT, mentre è indicato con s nel programma MINITAB e root MSE nel SAS.