CORRELAZIONE  E  COVARIANZA

 

 

18.14. L'ANALISI DEI RESIDUI PER L'IDENTIFICAZIONE DEGLI OUTLIER; RESIDUALS, STUDENTIZED RESIDUALS, STANDARDIZED RESIDUALS

 

 

Nella regressione, un outlier può essere definito come l’osservazione che produce un residuo molto grande. Alcune tecniche semplici sono riportate da

-   James E. De Muth nel suo testo del 1999 Basic Statistics and Pharmaceutical Statistical Applications (edito da Marcel Dekker, Inc. New York, XXI + 596 p. a pag. 538 - 543).

Ad esso si rimanda per approfondimenti. I metodi sono presentati con lo sviluppo di un esempio, qui riportato con maggiori dettagli nei passaggi logici.

 

Nello studio di un fenomeno di fermentazione, in cui

-   rappresenta la concentrazione della sostanza, (prima riga),

-   è la quantità fermentata nell’unità di tempo (seconda riga),

-    è la quantità stimata sulla base della retta di regressione calcolata:  (terza riga),

-    indica lo scarto tra i due valori della variabile Y:  (quarta riga)

 come i dati della tabella seguente

 

 

 

 

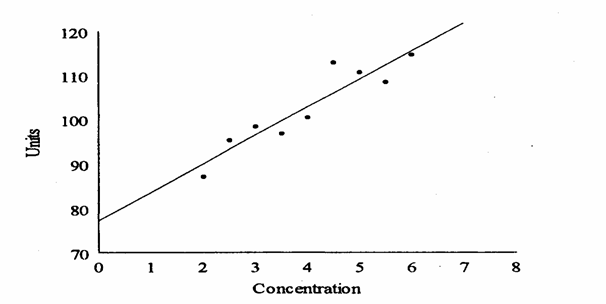
 l’analisi degli outlier richiede dapprima una lettura del diagramma di dispersione dei punti osservati   e   (vedi pagina successiva), rispetto alla loro retta di regressione.

 

 

Ad occhio,

-   il punto di coordinate  = 4,5  e  = 112,9 che determina lo scarto maggiore ( = +6,895)

-   non appare così distante dagli altri da poter essere giudicato un outlier.

Ma

-  la distanza del punto  = 112,9 dalla sua proiezione sulla retta = 105,905 non semplice da valutare. Soprattutto, per decidere, si richiedono test che permettano di stimare la probabilità a.

 

Come prima analisi, con i dati  e , è importante verificare la significatività della retta di regressione

H₀:  = 0          contro          H₁:  ¹ 0

 Con il calcolo di F si ottiene:

 

 

 

La tabella dei risultati (F = 43,78 per df 1 e 7, con P < 0.001) dimostra che linearità è altamente significativa. Attraverso la varianza d’errore ( = 13,90), è poi ricavabile un valore importante per l’analisi dei residui,

-  la deviazione standard degli errori (),

 che in questo caso risulta

 

Nella figura precedente, a una valutazione occhiometrica, il valore di Y per X = 4,5 non appariva molto distante dagli altri. Ma è un outlier oppure solo un valore estremo in una distribuzione normale?

Utilizzando la retta di regressione (non sono riportati i suoi parametri) si calcolano

-  i valori attesi ( nella terza riga della tabella)

-  e per differenza i residui o errori ( nella quarta riga della tabella; in molti testi indicati con ).

Con la serie dei residui , si è ritornati a dati univariati. Quindi con essi sono possibili tutte le analisi già presentate per la statistica univariata, a partire dagli istogrammi e dal Box and Wiskers di Tukey.

 

 

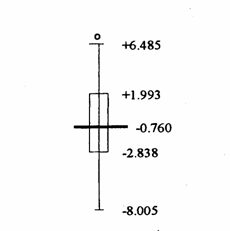
Secondo i calcoli di Tukey e come appare in questa  figura si ottiene una prima risposta:

-  il cerchio vuoto che identifica il residuo maggiore (+6,895) è un outlier, in quanto è superiore al valore VAS (+6,485) o cinta interna o inner fence. (Rivedere i paragrafi della univariata).

Ne consegue che il punto corrispondente, di coordinate ( = 4,5  e   = 112,9), è giudicato statisticamente un outlier.

La sua presenza rimetterebbe in discussione la validità della regressione calcolata in precedenza e quindi la significatività dell’analisi, che richiedono la normalità della distribuzione degli errori.

 

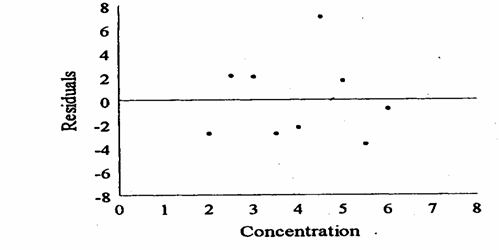
Per facilitare la lettura statistica del grafico dei residui, è prassi utilizzare una loro rappresentazione standard che rimedia alle difficoltà precedenti, poiché è indipendente dalla collocazione (intercetta ) e dalla pendenza della retta (coefficiente angolare ). 

In questo grafico (nella pagina successiva),

-  la retta è sempre orizzontale, parallela all’asse delle ascisse sulla quale sono riportati i valori ,

-  mentre i valori dei residui sono letti sull’asse delle ordinate.

 

Diventa più semplice osservare che

-  la distanza del punto outlier dalla retta orizzontale appare con evidenza maggiore,

 rispetto al precedente diagramma di dispersione, costruito con i dati originali distribuiti intorno alla retta di regressione.

Con chiarezza ugualmente maggiore, risulta una proprietà importante dei residui (già rimarcata nella tabella):

- la loro somma è uguale a zero.

 

 

 

Un’altra convenzione diffusa nell’analisi degli outlier, in quanto facilita il confronto tra variabili diverse e casi differenti uniformando le dimensioni, è la trasformazione dei residui in residui studentizzati (studentized residuals).

Essa rende uguale  la scala di valutazione,

 attraverso la relazione

Ad esempio,

 riprendendo la tabella dei dati, il primo residuo ( = -2,840)

 diventa

 

 un residuo studentizzato t = -0,762.

 I precedenti  risultano trasformati in   studentizzati come nella tabella successiva:

 

 

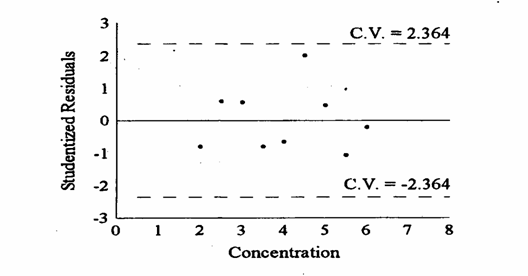
Anche di questi residui studentizzati (studentized residuals) è bene fare la rappresentazione grafica (utilizzando i valori della prima e della terza riga della tabella precedente). Nel grafico, senza essere espressamente dichiarato, con la presenza delle due linee tratteggiate è riportato anche il risultato di un altro test su gli outlier, che è bene esplicitare.

 

 

 

 

Il valore C.V. = 2,364 (con segno positivo e negativo sopra le linee tratteggiate, parallele alla media)

-   è il valore critico del t di Student con 7 gradi di libertà,

-  per la probabilità a = 0.05 in una distribuzione bilaterale (nelle tabelle allegate in realtà è 2,365).

In questa rappresentazione grafica dei residui studentizzati, è reso visibile un concetto:

 i residui studentizzati, ottenuti con

 

sono altrettanti test t

- in cui, con i dati dell’esempio, nessun residuo supera  il valore critico (2,364),

Hanno gradi di libertà , poiché sono residui intorno alla retta di regressione, per tracciare la quale servono due punti.

 

A differenza del precedente metodo di Box and Wiskers, in questo secondo test

-  nessun residuo risulta essere un outlier,

-  se il valore critico è scelto alla probabilità a = 0.05 in una distribuzione bilaterale.

Quindi non è significativo quel punto che, con il precedente test di Tukey, risultava un outlier (+6,985). In questo caso, il metodo dei residui studentizzati fornisce un valore (+1,874) nettamente inferiore a quello critico (2,364).

Ma l’analisi t di Student con k residui solleva il problema del principio del Bonferroni, che spesso su questi problemi viene trascurato. Per ogni confronto t di Student,

-  la probabilità a’ da utilizzare dovrebbe essere la probabilità totale a_T = 0.05 divisa per k.

 

I residui studentizzati, anche se solamente su alcuni testi, in modo non appropriato sono chiamati anche residui standardizzati (standardized residuals). Per questi ultimi, al posto della devianza standard campionaria , è utilizzata

-  la deviazione standard della popolazione .

 

Quando il campione è molto grande, i residui studentizzati e i residui standardizzati tendono a coincidere, come il valore t di Student tende a convergere verso il valore della Z.

Rimane la difficoltà di definire quando un campione è sufficientemente grande. Nella pratica sperimentale, spesso questa tecnica è utilizzata anche con campioni piccoli.

Con i residui standardizzati, al posto del valore critico t di Student che ha gradi di libertà (), si utilizza la distribuzione Z. I suoi valori critici sono sempre minori del t.

Ad esempio, alla probabilità a = 0.05

-  per i residui studentizzati è stato utilizzato come valore critico  t = 2,364 (con gdl = 7)

-  mentre per i residui standardizzati il valore critico corrispondente è  Z = 1,96.

 

Tuttavia, nell’analisi degli outlier spesso vengono utilizzate stime approssimate. Quindi

- per la probabilità a = 0.05 con i residui standardizzati viene assunto il valore 2, non 1,96..

Ma la probabilità (5%) corrispondente è alta: verrebbero indicati come outlier valori che frequentemente non li sono.

Ne consegue che, per decidere che un dato è un outlier, è prassi diffusa utilizzare 3 come valore critico e non 2 (vedi outlier nella statistica univariata). La probabilità P è nettamente minore di 0.05.