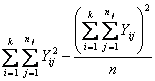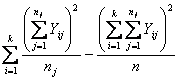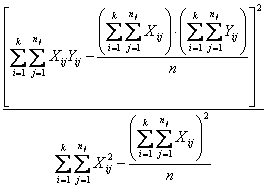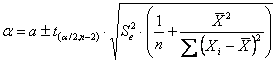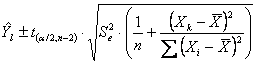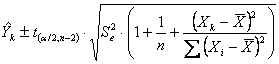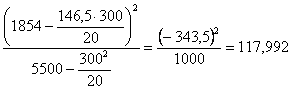CONFRONTI TRA RETTE,

CALCOLO DELLA RETTA CON Y RIPETUTE, CON VERIFICA DI LINEARITA’ E

INTRODUZIONE ALLA REGRESSIONE LINEARE MULTIPLA

 

 

 

17.5.  ANALISI DELLA RELAZIONE DOSE-EFFETTO CON Y ripetute: Calcolo della retta di regressione E TEST PER LA LINEARITA'.

 

 

Nella ricerca di laboratorio e nella verifica di un prodotto farmacologico, spesso si richiede di saggiare la risposta biologica a dosi variabili di un principio attivo, sia esso un farmaco o un tossico. Si impostano esperimenti nei quali vengono somministrate quantità progressivamente crescenti, per verificare come varia la risposta media in gruppi di cavie o pazienti.

In altri casi, si analizza come

-  gli effetti di una dose variano nel tempo o come una sostanza attiva si degrada.

 

Con valori di Y ripetuti per la stessa dose X, l’analisi della regressione prevede che, per attuare la scelta più adeguata fra i vari tipi di curve, si risponda a 4 domande:

1 – Il farmaco ha un’azione che varia con la dose?

2 – La risposta è proporzionale alla dose? In termini più tecnici, esiste regressione della risposta sulla dose?

3 – La regressione è di tipo lineare oppure può essere meglio espressa da una curva di grado superiore?

4 – Se non è lineare, quale è il tipo di curva più adeguato?

 

Queste quattro domande richiedono l’applicazione di quattro test.

 

A - Il primo è un'analisi della varianza ad 1 criterio di classificazione. Affinché l’analisi della regressione sia giustificata, deve esistere variabilità nelle risposte medie: il test sulla differenza tra le medie deve risultare significativo.

 

B - Il secondo è il test per la linearità, che ha lo scopo di valutare se una retta di regressione si avvicina ai punti medi delle risposte (), fornite per la stessa dose (), in modo significativo rispetto alla media generale () delle Y. Anche in questo caso, sempre per giustificare il calcolo della retta, il test deve risultare significativo.

 

C - Il terzo è il test per la non-linearità, allo scopo di verificare se curve di grado superiore passino più vicino ai punti medi delle risposte () per la stessa dose () in modo significativo rispetto alla retta. Si parla di verifica dei “termini non lineari” o degli “scarti dalla regressione”. Per poter concludere che la retta è la stima migliore della relazione dose - risposta, questo test deve risultare non-significativo.

 

D - Se invece risulta significativo, mediante l’uso dei coefficienti polinomiali per l’analisi delle regressioni, con un quarto test si deve valutare quale sia il tipo di curva più adeguata, anche se quasi sempre si sceglie quella di secondo grado.

 

A causa della semplicità di interpretazione e al fatto che solo esse sono generalmente valide in quasi tutte le situazioni sperimentali, le preferenze dei ricercatori vanno alla retta e alla curva di secondo ordine. Quelle più complesse, di ordine superiore, sono regressioni troppo specifiche, sono troppo legate ai dati campionari per esprime una legge universalmente valida.

 

In questo paragrafo, sono presentati i concetti e i metodi che rispondono alle prime tre domande. Per la quarta, su come valutare quale sia la curva più adeguata, è possibile utilizzare i coefficienti polinomiali, che rappresentano il metodo più semplice e rapido. I concetti e i metodi sono esposti nel paragrafo successivo.

 

Nella impostazione di un esperimento in cui si richieda l’analisi della regressione con Y ripetute, il primo problema è quanti gruppi formare. Se, oltre al calcolo della retta di regressione lineare semplice, si intende effettuare anche le analisi successive sui termini non lineari, è vantaggioso che i gruppi siano almeno 4. Spesso come massimo sono 6, in quanto le informazioni aggiuntive sono ridotte e non giustificano i tempi e i costi dell’esperimento.

 

Per la scelta del numero di gruppi, è necessario decidere anticipatamente quale sia il tipo di curva desiderato e il livello della verifica. Infatti

- tra due soli punti passa una retta, rappresentata da un’equazione di primo grado:

 

- fra tre punti si può fare passare una linea, rappresentata da un’equazione di secondo grado:

 

- tra quattro punti si può fare passare una linea, rappresentata da un’equazione di terzo grado:

 

 - e così di seguito, fino ai 5-6 punti medi programmati.

Nell’analisi della regressione lineare semplice, l’operazione richiesta consiste nell’isolare il termine lineare.

 

Tra le applicazioni della regressione, lo studio delle risposte a dosi progressive di una sostanza attiva è la più frequente e forse la più importante. Ottenere, come desiderato, una retta non sempre è facile. La linea che esprime la relazione tra gli effetti medi () di dosi crescenti di una sostanza attiva () raramente è perfettamente lineare, anche su in intervallo breve, se la scelta dei dosaggi non è predisposta in modo accurato e centrata.

Spesso se ne discosta in modo rilevante, poiché

-  dosi molto piccole producono effetti nulli o difficilmente rilevabili, in quanto collocati sotto il livello di soglia;

- solo dosi medie producono effetti crescenti;

-  dosi elevate forniscono spesso la risposta massima, avendo raggiunto la saturazione.

 

Per ottenere la linearità, è vantaggioso che

- le dosi somministrate seguano una progressione pertinente al problema duisciplinare che si affronta.

Essa può essere scelta entro una varietà ampia.

Nel paragrafo successivo, dedicato all’uso dei coefficienti polinomiali, sarà richiesto necessariamente.

Ad esempio, può essere di tipo

-  lineare  2,  4,  6,  8, 10   (2, +2 .. );   3,  6,  9, 12, 15 (3, +3…);

-  esponenziale o logaritmica 2,  4,  8,  16,  32   (2¹,  2²,  2³,  2⁴, 2⁵)

-  o ancora  1,  4,  9,  16,  25   (1²,  2²,  3²,  4²,  5²),

-  ma anche 1,41;   2,00;    2,45;    2,83;   3,16   (,  ,  ,  ,  )

 oppure qualsiasi altra progressione.

 

Tra queste, per ottenere un arco sufficientemente ampio di risposte con poche dosi, spesso è preferito il logaritmo della dose (2,  4,  8,  16,  32). Infatti è dimostrato che, nella maggior parte delle attività biologiche, l’effetto aumenta con progressione aritmetica, quindi lineare, quando la sostanza attiva è somministrata in proporzione geometrica.

Ma non sempre questa legge è vera; non per tutti i principi attivi, non per tutti i dosaggi somministrati, né per tutti i fenomeni biologici.

Da qui l’importanza di testare sempre la linearità della regressione dell’effetto sulla dose o su una trasformazione qualsiasi della dose.

 

In molte discipline,

- il calcolo e l’analisi della regressione non include necessariamente il concetto di una relazione di causalità tra la X e la Y, né che essa sia nella direzione segnalata implicitamente dalla indicazione di variabile X (la causa) e variabile Y (l’effetto).

Spesso, si vuole semplicemente

- utilizzare la capacità predittiva della regressione per stimare Y conoscendo X, allo scopo di ottenere la descrizione di una relazione empirica in un campione; successivamente si effettua il test, come controllo della sua esistenza anche nella popolazione.

 

Nel caso in cui si abbiano più osservazioni  per lo stesso valore di , lo scarto di ogni punto  dalla retta  (quindi ) può essere separata in due parti:

1 - lo scostamento dell'osservazione  dalla media del suo gruppo  (quindi ),

2 - lo scostamento della media  del gruppo dal valore stimato sulla retta  per la stessa  (quindi ).

Tra essi esiste la relazione

 

Da questa relazione deriva che la devianza residua o di errore della retta di regressione,

 che nel caso di singole  per ogni  è  ,

 nel caso di  ripetute è scomponibile in

- una prima devianza, dovuta alla dispersione dei singoli valori intorno alla media del loro gruppo, cioè    e che rappresenta l’errore

-  e una seconda devianza, dovuta alla dispersione delle medie dalla retta di regressione e che rappresenta i termini non lineari,

cioè    .

 

 Con  ripetute per lo stesso ,

 tra queste devianze esiste la relazione

 

Quando l'analisi della varianza porta alla conclusione che esiste una differenza altamente significativa tra le medie  dei gruppi, sussiste la condizione logica per verificare, mediante una ulteriore specifica analisi della varianza, se sia di tipo lineare.

 

Per questi test sulla linearità, si richiedono le seguenti stime:

1 - la devianza tra gruppi (df = k-1) ottenuta con l'analisi della varianza;

2 - la devianza dovuta alla regressione (df = 1), chiamata anche della regressione lineare,

 mediante

 

3 - la devianza delle medie dalla regressione (df = k-2), chiamata anche della regressione non-lineare, è ricavabile dalla relazione

Devianza delle medie dalla regressione = Devianza tra gruppi - Devianza della regressione;

 

4 - la devianza residua entro gruppi o errore (df = n-k) ricavabile da

Devianza d’errore o residuo = Devianza totale - Devianza tra gruppi

 ricordando che,

 con la consueta simbologia,

-   = numero di gruppi

-   = numero di repliche del gruppo ;  

-   = numero totale di osservazioni

 

Le devianze sono calcolate più facilmente e rapidamente con le formule abbreviate.

Una presentazione sintetica e chiara di questi metodi è fornita dalla tabella

 

 

 

Dopo il calcolo delle varianze relative, con le ultime tre (della regressione, delle medie dalla regressione e residuo entro gruppi) si effettuano 2 test F.

Il primo F con df 1  e  n-k

 

 per verificare l'ipotesi nulla  ovvero se la regressione lineare sia significativa (rispetto alla media).

 

Il secondo F con df k-2  e  n-k

 

 per verificare l'ipotesi se esistano curve di ordine superiore che siano in grado di rappresentare in modo significativamente migliore della retta la relazione esistente tra dose e risposte medie.

 

Per gli intervalli di confidenza della retta, cioè per il calcolo

-  dell’intervallo di confidenza del coefficiente angolare

 

 

-  dell’intervallo di confidenza della intercetta

 

 

-  dell’intervallo di confidenza di un valore medio di  per la specifica dose

 

 

-  dell’intervallo di confidenza di un singolo valore di

 

 

 si utilizza la varianza d’errore o residuo   e la devianza delle X   .

Nell’esempio successivo  = 0,3783  e la devianza delle X è   = 1.000.

 

 

ESEMPIO   E’ dimostrato che l'inquinamento da cromo in dosi subletali agisce in modo negativo sull'accrescimento somatico di molte specie acquatiche.

Con un esperimento di laboratorio, si vuole stabilire la relazione che intercorre tra la concentrazione della sostanza e la risposta biologica in alcuni gruppi di crostacei della stessa specie, dei quali vengono fornite le dimensioni dopo una settimana dalla schiusa delle uova.

Le dosi sono crescenti in modo lineare: 5, 10, 15, 20, 25.

 

Le repliche (da I a IV) considerano 4 casi per gruppo

 

 

 

 

Verificare se l’effetto risente della somministrazione di dosi diverse; in caso positivo, stimare se la retta è adeguata a descrivere la relazione dose-effetto.

 

Risposta.  Per rispondere ai quesiti proposti, la prima verifica è l'analisi della varianza ad un criterio di classificazione.

Dopo aver calcolato le somme delle Y per ogni gruppo e la somma totale dei quadrati delle Y (le medie servono per il grafico)

 

 

 

 

 si ricavano

-  la devianza totale con df = 19

 

-  la devianza tra gruppi con df = 4

 

 

-  la devianza entro gruppi o errore con df = 15

 

 

I risultati sono riportati nel solito schema dell’analisi della varianza

 

 

 

 

 Per valutare se esiste un effetto differente alle varie dosi,

 si calcola un test F

 che risulta uguale a 82,78 con df 4 e 15.

 

Se il test F non risultasse significativo e pertanto non permettesse di rifiutare l'ipotesi nulla, si deve giungere alla conclusione logica che, al variare della dose, le risposte medie dei gruppi a confronto non manifestano differenze significative. Di conseguenza, la media generale rappresenta la stima lineare migliore dell'effetto medio delle varie dosi ed è inutile procedere al calcolo della retta di regressione.

In questo caso, poiché il valore tabulato di F_(4,15) per  = 0.01 è uguale a 4,89 si deve concludere che le risposte differiscono in modo significativo al variare della dose. In modo più preciso, la probabilità è inferiore a 0.001.

Le due domande successive sono:

-  La retta rappresenta una stima accettabile dell’effetto biologico al crescere della dose?

-  Oppure è più adeguata una curva di grado superiore?

Alla prima si risponde mediante il test per la linearità, per il quale è necessario calcolare la devianza dovuta alla regressione lineare

 

SQ dovuta alla regressione lineare =

 

 

Con i dati dell’esempio

 

 = (5 x 45,3) +(10 x 35,3)+ (15 x 27,6)+ (20 x 19,4)+ (5 x 18,9) = 1.854

 = 4(5 + 10 + 15 + 20 + 25) = 300

 = 4(5² + 10² + 15² + 20² + 25²) = 5500

 = 146,5

 

 si ottiene

 

SQ dovuta alla regressione lineare =

 

Riportando questo risultato nella tabella precedente, si ottiene una nuova tabella che evidenzia:

 

 

 

 

-  la scomposizione della devianza tra gruppi (125,265) con df = 4

-  in devianza dovuta alla regressione lineare (117,992) con df = 1

- e, per differenza, in devianza  dovuta alla regressione non-lineare (7,273) con df = 3

 

 Per  valutare se la retta di regressione rappresenta un miglioramento significativo rispetto alla media generale delle Y,

 si effettua un test F

 

Con i dati dell’esempio, si ottiene F = 311,9 con df 1 e 15.

Esso dimostra che la regressione lineare semplice è altamente significativa: la retta passa molto più vicino alle medie dei 5 gruppi di quanto faccia la media generale. Di conseguenza, è molto vantaggioso calcolare la retta, per evidenziare la relazione tra dose e risposta media.

 

Per valutare se una curva di grado superiore rappresenta una stima statisticamente migliore si effettua un secondo test F

 

Con i dati dell’esempio, si ottiene F = 6,41 con df 3 e 15 che risulta significativo.

E’ statisticamente dimostrato che una curva di grado superiore si avvicina alle medie delle 5 dosi in modo significativamente migliore della retta.

 

Riassumendo i concetti illustrati nel paragrafo, all’inizio è stato evidenziato che con Y ripetute l’analisi della varianza permette di rispondere a  4 domande

1 – Il farmaco ha un’azione che varia con la dose?

2 – La risposta è proporzionale alla dose? In termini più tecnici, esiste regressione della risposta sulla dose?

3 – La regressione è di tipo lineare oppure può essere meglio espressa da una curva di grado superiore?

4 – Se di grado superiore quale è il tipo di curva più adeguato?

 

Con le analisi fino a ora condotte si è risposto alle prime tre, arrivando alle conclusioni seguenti:

1 - Le risposte biologiche alle varie dosi sono significativamente differenti.

2 – Le risposte sono proporzionali alle dosi e una retta descrive in modo significativamente più accurato della media la relazione tra dose e risposta.

3 – Ma una curva di grado superiore la descrive in modo significativamente migliore della retta.

 

 

La rappresentazione grafica delle singole risposte alle varie dosi e delle loro medie evidenzia visivamente come la retta passi effettivamente molto più vicino ai punti medi, di quanto faccia la media generale delle Y.

 (I cerchi vuoti rappresentano le singole osservazioni. Sono quattro per gruppo, ma appaiono in numero minore poiché in alcuni casi risultano sovrapposti.

I cerchi neri sono le medie dei singoli gruppi)

 

I valori medi non sono collocati esattamente sulla retta. Questa non esatta linearità lascia inoltre intuire come

-  una curva di grado superiore possa effettivamente passare più vicino a essi di quanto faccia la retta.

 

Ma per rispondere in modo dettagliato alla quarta domanda (Se è di grado superiore, quale è il tipo di curva più adeguato?)

- è necessario valutare il contributo che ognuna delle 3 curve di ordine superiore fornisce alla devianza dovuta ai termini non lineari:

Questa risposta richiede calcoli lunghi e complessi, molto più di quanto sia stato fatto per la regressione lineare.

 

Nel paragrafo successivo, sono presentati i coefficienti polinomiali, che sono il metodo più semplice e rapido

-  sia per calcolare la devianza dovuta alla regressione lineare, fornendo lo stesso risultato già ottenuto,

- sia per calcolare la devianza dovuta a ogni curva di grado superiore.