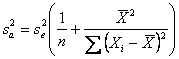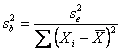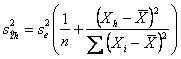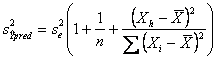CONFRONTI TRA RETTE,

CALCOLO DELLA RETTA CON Y RIPETUTE, CON VERIFICA DI LINEARITA’ E

INTRODUZIONE ALLA REGRESSIONE LINEARE MULTIPLA

 

 

 

17.11.   SCELTA DEI VALORI DI X,  PER UNA REGRESSIONE SIGNIFICATIVA

 

 

Come scegliere i dati per effettuare un test statistico è parte del campionamento, discusso nei capitoli finali del corso. Infatti, benché debba essere programmato prima dell’esperimento, un campionamento corretto richiede la esatta conoscenza sia del tipo di scala per la misure che verranno effettuate sia della metodologia dei test che sono programmati. Tuttavia, già

-  nella presentazione del test t di Student per  il confronto tra la media di un campione e una media attesa oppure per il confronto tra due medie,

-  nell’analisi della varianza per il confronto tra due o più medie,

-  nei test per il confronto tra le varianze di due o più campioni,

 il concetto implicito nella raccolta dei dati campionari è sempre che essi siano rappresentativi di quelli della popolazione.

Un modo, il più semplice, è l’estrazione casuale o random dalla popolazione, che ha valori ignoti. Per effettuare un campionamento corretto, non è necessario conoscere i valori della popolazione e spesso esso è condotto nella totale ignoranza dei parametri della distribuzione.

 

Nel caso della regressione, il campionamento deve essere effettuato dopo una attenta analisi dei valori della variabile X, che quindi devono essere noti. Diversi testi, tra i quali il volume di Neter John, Michael H. Kutner, Christofer J. Nachtsheim, William Wasserman del 1996 Applied Linear Statistical Models (fourth ed.,  WBC/McGraw-Hill, Boston, 1400 pp.), ne illustrano i principi e le modalità.

Il valore o livello di X deve essere scelto dallo sperimentatore, sulla base dell’uso della regressione. Ad esempio, per la regressione tra dose del farmaco (X) e effetto (Y), può essere necessario rispondere a quattro domande:

 1 -  Quali livelli di X devono essere analizzati?

 2 -  Quali sono i due valori estremi, entro il cui intervallo interessa la regressione?

 3 -  Con quali intervalli scegliere le singole dosi X?

 4 -  Quante osservazioni effettuare per ogni dose X?

 

Le risposte dipendono dal tipo di regressione che si vuole effettuare e dal parametro che si vuole prima misurare e poi testare. Ad esempio, se interessa solamente il coefficiente angolare b, oppure solamente la intercetta a, oppure entrambi; inoltre, se la regressione cercata è lineare oppure curvilinea e di quale ordine.

Comunque esistono indicazioni generali, che sono meglio comprese attraverso una lettura delle formule che permettono per calcolare le 4 varianze che possono essere utilizzate, sia nei test, sia per la stima degli intervalli di confidenza. Con la simbologia consueta, esse sono

- la varianza dell’intercetta a

 

- la varianza del coefficiente angolare b

 

 

- la varianza del valore medio di Y stimato ()

 per la singola dose X_h

 

- la varianza del singolo valore di Y stimato o predetto ()

 per la singola dose X_h

 

In tutte le formule, al denominatore compare la devianza della variabile X,

cioè

 che deve essere massima, affinché la varianza sia minima.

Di conseguenza, per ottenere la precisione massima per una stima e la potenza massima per un test, è vantaggioso che la variabilità dei valori della X sia massima. Quindi, la scelta dei valori della X non deve essere casuale, ma

 -  prima si devono analizzare i valori presenti nella popolazione

- e successivamente scegliere quelli che determinano la varianza (,,,) sia minima.

Ne deriva che è errato scegliere valori di X tutti concentrati intorno alla loro media , con la motivazione che essi indicano la dimensione normale del fenomeno, quindi quella che riveste maggior interesse, poiché i valori estremi di X sono riscontrati più raramente e spesso indicano valori atipici.

Se è già certo che la regressione sia di tipo lineare e si tratta solo di calcolare il coefficiente angolare e la sua significatività o il suo intervallo di confidenza, è vantaggioso che metà delle osservazioni siano collocate intorno al valore minimo della X e l’altra metà intorno al valore massimo.

 

Per valutare invece se esista linearità o sia più adatta una curva di ordine superiore, è bene che i valori di X siano collocati a intervalli regolari, usando 4 livelli se il tipo di curva cercato è di secondo ordine con forma a parabola. Usare 5 o 6 livelli, quando la curva può essere di tipo asintotico oppure essa non è adeguatamente descritta da una curva di secondo ordine, ma di terzo ordine. In questi casi, è vantaggioso che il campionamento per Y ripetute che sia bilanciato, poiché l’errore standard, dato dallo scarto di ogni Y dalla sua media  per la stessa X, è minimo quando il numero di osservazioni è sempre uguale.

 

Se la regressione è effettuata per stimare il valore e verificare la significatività l’intercetta a, nel calcolo della sua  varianza () il valore  diventa più importante della devianza , in quanto spesso può essere molto grande. Ne consegue che è vantaggioso che la media delle X sia vicina a 0, con un valore ideale di .

Se invece si desidera stimare

-  il valore medio di Y per una singola dose h di X () oppure

- una singola risposta di Y sempre per la dose h di X ()

 è vantaggioso che, oltre a tenere in considerazione la devianza, la dose scelta di X sia a distanza minima dalla media, con un valore ideale di.