LA REGRESSIONE LINEARE SEMPLICE

16.20. ANALISI DELLA VARIANZA A DUE CRITERI, MEDIANTE IL METODO DELLA REGRESSIONE.

Come illustrato nel paragrafo precedente, nei test di significatività l’analisi della varianza e la regressione sono equivalenti.

Con tale giustificazione, molti programmi informatici recentemente hanno divulgato test dell’analisi della varianza che, abbandonata l’impostazione classica del calcolo delle devianze adottata anche in queste dispense, ricorrono solo all’analisi della regressione lineare e forniscono output che disorientano gli utenti, che si aspettano la risposta tradizionale riportata sui testi.

	TRATTAMENTI (ZONE)
BLOCCHI (ORE)	A	B	C	D	E
I	28	25	30	22	26
II	34	32	37	31	30
III	22	21	24	20	19
IV	36	31	40	33	29

Ad esempio, l’analisi della varianza crossed a due criteri di classificazione applicata ai dati della tabella precedente per valutare la significatività delle differenze

- tra le medie dei trattamenti e

- tra le medie dei blocchi,

nell’output tradizionale dei programmi informatici fornisce i risultati della tabella successiva

Analysis of Variance Procedure

Dependent Variable: VY

Sum of Mean

Source DF Squares Square F Value Pr > F

Model 7 654.3000000 93.4714286 39.08 0.0001

Error 12 28.7000000 2.3916667

Corrected Total 19 683.0000000

R-Square C.V. Root MSE VY Mean

0.957980 5.426321 1.546501 28.5000000

Source DF Anova SS Mean Square F Value Pr > F

BLOCCHI 3 525.8000000 175.2666667 73.28 0.0001

TRATTAM 4 128.5000000 32.1250000 13.43 0.0002

In essa, lo studente non ha difficoltà a trovare, con i loro gradi di libertà,

- la devianza totale,

- la devianza tra trattamenti,

- la devianza tra blocchi,

- la devianza d’errore,

e a individuare tutti i parametri da essi derivati, dalle varianze ai test F, alle probabilità P.

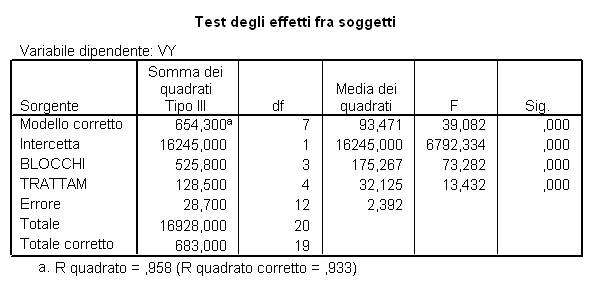
Ma in altri programmi informatici, a volte compresi nelle stesse librerie statistiche, la medesima analisi è fornita con l’output successivo.

Vi si riscontrano tutti i parametri precedenti dell’ANOVA.

Ma è semplice osservare che sono state inserite altre due voci, quelle appunto “inspiegabili” e che pertanto disorientano, nella lettura di un output sull’analisi della varianza:

- Intercetta = 16245,000 con df = 1

- Totale = 16928,000 con df = 20

che fanno pensare alla regressione lineare e quindi alla individuazione di una retta.

Ma non comprendendo dove la retta (non richiesta) sia collocata, all’utente iniziale non è evidente

- come sia calcolata la quantità attribuita all’intercetta, con un grado di libertà ,

- e conseguentemente che cosa si debba intendere per Devianza Totale con df = n.

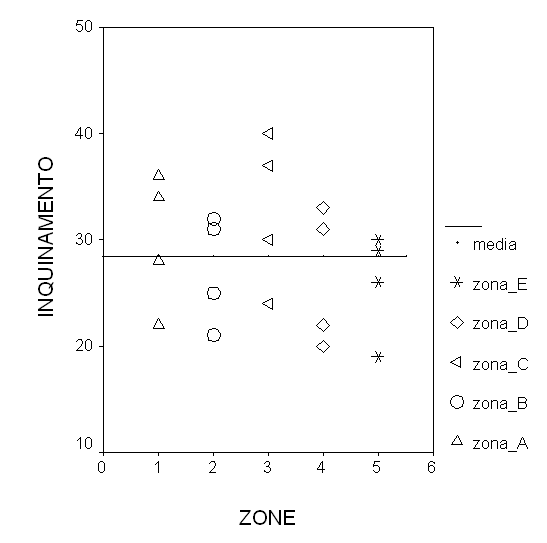
La figura riportata nella pagina successiva è la rappresentazione grafica dei valori riportati nella tabella iniziale dei dati, analizzati con questi due programmi informatici. Nella figura sono facilmente leggibili

- i quattro dati per ognuno dei 5 gruppi (A, B, C, D), rappresenti da 5 simboli differenti,

- la media generale di tutti i dati (28,5 sull’asse delle ordinate), rappresentata dalla retta a metà del grafico.

Con la lettura della tabella e l’aiuto fornito dalla figura è semplice comprendere che

1 - l’intercetta è semplicemente la media generale delle Y (= 28,5), che nella figura è la retta;

(In programmi di sola analisi della varianza, i dati sono quasi sempre indicati con X; se per la stessa analisi si usa la regressione lineare, dalla statistica univariata si passa a quella bivariata e la variabile analizzata diventa la variabile dipendente, da indicare quindi sempre con Y.)

2 - la devianza ad essa attribuita (16245,000) con df = 1 è il quadrato dello scarto della media dall’asse delle ordinate (quindi da Y = 0) calcolato per ogni valore di Y:

dove = 20 e = 28,5.

3 - la devianza totale (16928,000) con df = 20 pertanto è la somma

Totale = Intercetta + Totale corretto

Di conseguenza, la sovrapposizione dei risultati stampati nelle due tabelle è totale,

- se si ignorano i valori riferiti alla Intercetta e al Totale

- e si utilizzano solamente gli altri cinque.