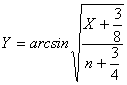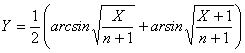trasformazionI dei dati;

test per normalita’ e PER OUTLIER

 

 

 

13.2.  ALCUNE TRASFORMAZIONI DEI DATI

 

 

Le trasformazioni riportate in letteratura e alle quali più frequentemente si ricorre sono:

-  la lineare,

-  la logaritmica,

-  le potenze, che comprendono le radici e soprattutto la radice quadrata e cubica, la reciproca e la quadratica,

-  le angolari,

-  i probit, i logit, i normit.

 

La trasformazione lineare consiste nel cambiamento di scala o dell’origine delle misure, per facilitare la loro comprensione delle caratteristiche dei dati o i calcoli da effetuare. Può essere moltiplicativa, additiva e una combinazione di queste due modalità. E’ il caso della trasformazione

-  della temperatura da gradi Celsius a Fahrenheit (trasformazione additiva e moltiplicativa),

-  di una lunghezza da pollici a centimetri m (trasformazione moltiplicativa),

- di una serie di dati che (ad es.) variano da 230 a 279 a valori da 1 a 49 (trasformazione additiva).

Questa ultima è la semplice sottrazione dello stesso valore a tutti i dati, che serve soprattutto per semplificare i calcoli.

In una trasformazione moltiplicativa, la variabile trasformata (X_T) è ottenuta con una semplice moltiplicazione della variabile originaria (X₀)

X_T = C×X₀

 dove C è la costante di conversione

(ad esempio, c = 2,54 per trasformare i pollici in cm e c = 0,394 nel capo opposto).

In questa trasformazione, seguono la stessa legge

- sia la media ()

- sia la deviazione standard e l’errore standard (indicati genericamente con S)

 

Non variando la forma della distribuzione né i rapporti tra media e varianza, la trasformazione lineare risulta inutile quando si intende modificare le caratteristiche fondamentali della distribuzione. A questo scopo, assumono importanza le trasformazioni non lineari, nelle quali a distanze uguali nella prima distribuzione non corrispondono distanze uguali anche in quella modificata.

Tutte le trasformazioni di seguito riportate, le più ricorrenti nelle applicazioni della statistica, non sono lineari.

 

 

La trasformazione in ranghi è una tecnica molto semplice, sempre più frequentemente raccomandata da autori di testi internazionali. Quando i dati sono abbastanza numerosi, utilizzare i ranghi al posto dei valori originari permette di ricostruire le condizioni di validità e di applicare tutti i test parametrici. Quando il campione è abbastanza numeroso (n > 30), i ranghi sono sempre distribuiti in modo normale; inoltre questa trasformazione elimina immediatamente l’effetto dei valori anomali.

E’ utile soprattutto nel caso di disegni sperimentali complessi, a tre o più fattori con eventuale interazione o analisi gerarchica, per i quali nella statistica non parametrica non esistono alternative ai test di statistica parametrica. Questo accorgimento permette anche di superare uno dei limiti fondamentali della statistica non parametrica, che offre test di significatività ma che raramente e con difficoltà è adattabile ai problemi, non meno importanti, di stima accurata dei parametri.

 

 

La trasformazione logaritmica

Y = log_a X

di solito avviene con base 10 o con base naturale (e), anche se non sono infrequenti quelli con base 2. Ha vari scopi.

Si applica quando la distribuzione ha simmetria positiva, per ottenere una distribuzione normale.

In variabili continue, è utile per rendere omogenee le varianze quando esse crescono all’aumentare della media.

Nel caso di effetti moltiplicativi tra variabili, come nell’interazione, per ritornare agli effetti additivi, richiesti dal modello statistico dell’ANOVA.

La tabella sottostante mostra come dati che possono variare da 2 a 20000 riducano il loro campo di variazione da 0,30 a 4,30 con logaritmi a base 10.

 

 

 

La scelta della base è secondaria.

Qualunque trasformazione logaritmica (ad esempio a base e oppure a base 2 oppure 10) determina effetti simili, anche se più o meno accentuati, poiché i dati trasformati differiscono solamente per una costante moltiplicativa.

 

Quando i coefficienti di variazione di gruppi a confronto sono approssimativamente costanti, le varianze aumentano in modo direttamente proporzionale alle medie; di conseguenza, confrontando i due gruppi A e B, tra i loro dati esiste la relazione

dove C è la costante della proporzione.

La trasformazione dei dati con i logaritmi

rende le varianze omogenee, poiché i dati avranno una media differente ma la stessa forma di distribuzione.

 

La trasformazione logaritmica può essere applicata solamente a valori positivi, in quanto non esistono i logaritmi di valori negativi.

Quando si hanno valori nulli, poiché log 0 = -(meno infinito), la trasformazione richiede l'accorgimento di aggiungere una costante (con C = 1 oppure C = 0,5) a tutti i dati (non solo a quelli nulli)

In varie situazioni, la trasformazione logaritmica ha effetti multipli: serve contemporaneamente a stabilizzare la varianza, a ridurre ad effetti additivi un effetto moltiplicativo, a normalizzare la distribuzione.

Si deve ricorrere alla trasformazione logaritmica quando si vuole ottenere una distribuzione normale da una distribuzione di dati caratterizzata da una forte asimmetria destra o positiva; si parla allora di distribuzione log-normale.

 

La trasformazione in radice quadrata

è uno dei casi più frequenti di trasformazioni mediante potenze, in cui c = 1/2.

E’ utile in particolare sia per normalizzare distribuzioni con asimmetria destra (ma meno accentuata rispetto alla trasformazione log) per omogeneizzare le varianze. Spesso è applicata a conteggi, quindi a valori sempre positivi o nulli, che seguono la distribuzione poissoniana.

In batteriologia, ematologia, fitosociologia è il caso di conteggi microbiologi oppure di animali o piante dispersi su una superficie. Poiché la varianza (npq) è proporzionale alla media (np), con i dati originali la condizione di omoschedasticità è spesso violata in partenza.

Quasi sempre i dati sono rappresentati da piccoli numeri, poiché all'aumentare della media la distribuzione poissoniana tende alla normale.

 

Quando si ha la  presenza di almeno uno zero è consigliabile (per tutti i dati)

 la trasformazione

che risulta appropriata per valori piccoli, con medie inferiori a 1, in cui la semplice trasformazione in radice quadrata determinerebbe un ampliamento delle distanze tra i valori minori.

Anche delle trasformazione in radice quadrata sono state proposte alcune varianti.

Per ridurre le relazioni tra varianza e media e quindi stabilizzare le varianze,

-  nel 1948 F. J. Ascombe (in The trasformation of Poisson, binomial and negative binomial data, pubblicato su Biometrika vol. 35, pp. 246-254) ha proposto

 

 

- nel 1950 M. F. Freeman e J. W. Tukey (in Transformations related to the angular and square root, pubblicato su Annals of Mathematical Statistics Vol. 21, pp. 607 - 611) hanno proposto

 

 particolarmente adatta quando X £ 2.

Ma, nonostante l’autorevolezza scientifica dei proponenti, nella pratica hanno avuto poca diffusione.

(Una  presentazione più ampia di questa trasformazione è riportata nel capitolo sulle condizioni di validità della  regressione e correlazione lineari).

 

La trasformazione in radice cubica

Y  = 

viene utilizzata per popolazioni che vivono in uno spazio tridimensionale. Come in ecologia per la distribuzione di animali sul terreno si usa la radice quadrata, in idrobiologia per conteggi di plancton che non risentano della crescita esponenziale di tali popolazioni si ricorre abitualmente alla trasformazione in radice cubica.

Nell’analisi di popolazioni che vivono in una spazio tridimensionale, si usa la trasformazione logaritmica quando ha la prevalenza la differenza stagionale, in specie che hanno esplosioni demografiche, per cui si possono avere campioni con poche unità ed altri con varie migliaia di individui; si usa quella in radice cubica se i dati presentano differenze minori e la distribuzione è asimmetrica.

 

La trasformazione reciproca

è particolarmente utile nell'analisi di tempi, come per confronti sulla sopravvivenza dopo somministrazione di un tossico ad elevata letalità o di reazione a stimoli. Di norma, la maggior parte delle reazioni cadono in un intervallo relativamente ristretto e con distribuzione approssimativamente normale; ma esistono anche individui che hanno tempi di reazione molto alti, con valori che alterano profondamente la distribuzione con una simmetria a destra.

Per tale asimmetria, sono quindi usate sia la trasformazione log sia quella in radice quadratica o cubica. La scelta tra esse dipende anche dalle caratteristiche della distribuzione dei dati.

La trasformazione reciproca serve per stabilizzare la varianza, quando essa aumenta in modo molto pronunciato rispetto alla media.

Quando uno o più individui non manifestano reazioni allo stimolo, il tempo diventa infinito: è impossibile fare la somma, calcolare la media e tutti le altre misure da essa derivate. La trasformazione reciproca, che attribuisce alla variabile Y = ¥  il valore zero, permette la stima di tutti parametri. Con essa, valori elevati di X corrispondono a valori di Y prossimi allo zero ed aumenti molto elevati in X producono effetti trascurabili in Y.

Per l'interpretazione sui risultati conviene ritornare alla scala originale, come per la media armonica.

Ad esempio, si supponga che i tempi di sopravvivenza in minuti di 5 insetti a una dose standard di DDT siano stati: 4, 5, 2, 10, ¥. Il quinto è sopravvissuto.

Quale è il tempo medio di sopravvivenza?

Dopo aver effettuato il reciproco ottenendo 0,25   0,20    0,50   0,10    0,0

 si ricava la media  1,05/5 = 0,21.

Si ritorna alla scala originale in minuti, attraverso la relazione 1/0,21 = 4,76.

 

La trasformazione quadratica

è utile in situazioni opposte a quelle fino ad ora presentate, cioè quando la varianza tende a decrescere all'aumentare della media e la distribuzione dei dati ha una forte asimmetria negativa.

Sono fenomeni rari nella ricerca ambientale e biologica. Pertanto, il suo uso è poco diffuso.

 

 

La trasformazione cubica

 si utilizza quando la asimmetria negativa è ancor più marcata. Ma i casi sono rarissimi.

 

La trasformazione angolare o in gradi mediante arcoseno

 quando p è la percentuale, altrimenti

quando p è la proporzione da 0 a 1

 oppure la  trasformazione seno inverso

Y = sen^-1  

 dove X è il numero di casi positivi su un campione di n dati.

Sono distribuzioni di tipo binomiale, che hanno un valore della varianza (pq) determinato da quella della media (p).

 

Per l’uso dei test parametrici, percentuali e frazioni presentano alcuni problemi, che richiedono analisi preliminari, poiché sono utilizzati per rendere le osservazioni indipendenti dalle dimensioni del campione. Per esempio, tra un primo esperimento che abbia fornito 3 risposte positive su 4 tentativi, un secondo che ne abbia dato 81 su 100 tentativi ed un terzo con 248 su 300 si può effettuare il confronto ricorrendo ai loro rapporti (rispettivamente 0,75 per il primo; 0,80 per il secondo; 0,83 per il terzo) oppure mediante percentuale (75%, 80% e 83%). Ma ognuno di questi dati ha una “attendibilità” diversa e un intervallo di confidenza differente; di conseguenza, non possono essere elaborati insieme.

Quando si dispone di percentuali e rapporti, occorre preliminarmente verificare su quali dimensioni del campione sono stati calcolati. L’analisi con test parametrici è accettabile solamente se le dimensioni sono relativamente simili: non è possibile elaborare insieme percentuali stimate su poche unità con altre stimate su un centinaio di individui od oltre. In statistica 3/4 non è uguale a 15/20, se con il primo si intendono 3 risposte positive su 4 individui ed con il secondo 15 risposte positive su 20.

Con questi dati è possibile solamente un test non parametrico, poiché la informazione reale fornita da una serie di tali valori è quella di rango.

 

Una volta che sia stato chiarito questo aspetto, occorre passare alla trasformazione angolare. Una proporzione con media p ha una varianza uguale a p(1-p): ha valori massimi per p prossimo a 0,5 e ha valori progressivamente minori per p che tende a 0 oppure a 1. La trasformazione angolare ha la caratteristica opposta: determina variazioni maggiori agli estremi che al centro della scala, riconducendo i rapporti tra le varianze a valori di omoschedasticità.

La proporzione p che varia da 0 a 1 (o la percentuale da 0 a 100% tradotta in proporzione) è espressa in gradi j che variano da 0 a 90, mediante la relazione già indicata. La tabella della pagina successiva permette di trasformare la proporzione direttamente in gradi.

 

Ad esempio,

- una proporzione p = 0,12 diventa j = 20,3

- una proporzione p = 0,75 diventa j = 60,0.

 

Questa trasformazione è poco precisa per valori di p prossimi a 0 oppure a 1. Per tali proporzioni sono proposte altre tabelle, anche se i computer e le semplici calcolatrici tascabili (utilizzando il simbolo sin^-1) spesso contengano questa trasformazione.

Nella tabella per valori estremi prossimi a 0, ad esempio,

- una proporzione p = 0,0012 (o 1,2 per mille)  diventa j = 1,99

- una proporzione p = 0,9958 (o 99,58%)  diventa j = 9,10.

Nella tabella per valori estremi prossimi a 1, ad esempio,

- una proporzione p = 0,95 (o 95%)  diventa j = 77,08

- una proporzione p = 0,025 (o 2,5%)  diventa j = 86,28.

 

TABELLA DI TRASFORMAZIONE DI PROPORZIONI (con p da 0,01 a 0,99)

IN GRADI j  (da 5,7 a  84,3)

j = arco seno

 

 

 

 

 

(Note)

Per ottenere valori più precisi, che considerino proporzioni alla terza cifra decimale, è sufficiente effettuare la stima mediante l’interpolazione lineare, ma solo per misure abbastanza grandi.

Per proporzioni piccole, utilizzare la relazione

 

Quando i valori di p sono simmetrici rispetto a 0,50 si ha che i valori in gradi sono simmetrici  rispetto a 45,0

Se la proporzione è grande, fare la trasformazione di p’ dopo il calcolo di p’ = 1-p.

 

TABELLA DI TRASFORMAZIONE DELLE PROPORZIONI PER VALORI ESTREMI:

DA  P = 0,0000   A   P = 0,0099   (PARTE SUPERIORE)

DA  P = 0,010   A   P = 0,100  (PARTE INFERIORE)

 

 

TABELLA DI TRASFORMAZIONE DELLE PROPORZIONI PER VALORI ESTREMI:

DA  P = 0,900   A   P = 0,989   (PARTE SUPERIORE)

DA  P = 0,9900   A   P = 1,0000   (PARTE INFERIORE)

 

 

La trasformazione delle proporzioni in arcoseno era già stata discussa da M. S. Bartlett nel 1947 (vedi l’articolo The use of transformations, su Biometrics, Vol. 3, pp.39-52) in cui per proporzioni p calcolate su campioni di n dati con X casi favorevoli, quindi p = X/n

 aveva proposto

 per proporzioni basse, vicine a 0,

 che diventa

 per il caso estremo di p = 0

 e dall’altra parte

 per proporzioni alte, vicine a 1,

 che diventa

 per il caso estremo di p = 1

 

Nel 1948, F. J. Anscombe, (nell’articolo The transformation of Poisson, binomial, and negative binomial data, pubblicato su Biometrika Vol. 35, pp. 246-254) come trasformazione migliore ha proposto la trasformazione in

 dove, con la simbologia precedente,

X è il numero di casi favorevoli in un campione di n dati.

Nel 1950, M. F. Freeman e J. W. Tukey (con l’articolo Transformations related to the angular and the square root, pubblicato su  Annals of Mathematical Statistics Vol. 21, pp. 607 - 611) hanno proposto un ulteriore raffinamento, quindi secondo alcuni preferibile,

 con

 

 che fornisce risultati molti vicini a quelli di Anscombe, eccetto per valori di p che siano estremi, molto vicini a 0 oppure a 1.

 

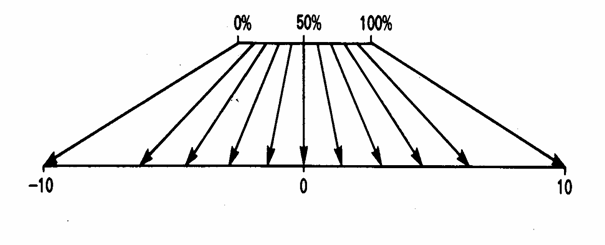
La trasformazione di percentuali o proporzioni con i differenti metodi presentati ha sempre l’effetto di ampliare le differenze verso gli estremi, come illustrato nella figura successiva

 

 

 

In essa a quella per omogeneizzare le varianze è stato aggiunta una trasformazione lineare, che non le modifica, ma fa in modo che il 50% diventi 0 e la distribuzione sia simmetrica intorno a esso.

E’ vantaggiosa a livello interpretativo quando il fenomeno atteso ha una  frequenza del 50%.

 

Le percentuali richiedono poi particolare attenzione nella interpretazione dei risultati.

Ad esempio, se un farmaco nuovo determina una riduzione del numero di decessi dal 3% a 1% e in una malattia diversa un altro farmaco determina una riduzione dei decessi dal 12% al 7% chi ha avuto il risultato migliore?

E’ vero che il primo ha abbassato la mortalità del 66% (2/3) e il secondo solo del 42% (5/12). Ma in termini di sopravvivenza, su 100 pazienti il primo ha determinato la sopravvivenza di due e l’altro di cinque persone. Ne consegue che è sempre importante presentare chiaramente il problema e lo scopo del confronto.

 

La trasformazione seno inverso iperbolico

Y =  sen h^-1

occupa una posizione intermedia tra la trasformazione logaritmica da applicare in variabili poissoniane altamente disturbate e la trasformazione in radice quadrata per variabili poissoniane standard.

 

La trasformazione tangente iperbolica inversa

Y = 1/2 log_e     =  tan h_r^-1

è analoga alla trasformazione logaritmica ed è applicata a variabili che variano da -1 a  +1.

E’ utile per normalizzare la distribuzione dei coefficienti di correlazione (r). Come vedremo, essi sono distribuiti normalmente solo per valori intorno allo zero, mentre diventano sempre più asimmetrici avvicinandosi ai valori estremi di  +1  e –1.

 

La trasformazione log-log

Y = log_e (-log_e p)

e la trasformazione log-log complementare

Y = log_e (-log_e (1-p))

si applicano a percentuali di sopravvivenza, nello studio dei tempi di eliminazione di un gruppo di cavie in dosaggi biologici.

 

La trasformazione probit

P  =    

(probits da probability units) è definita come la deviata normale equivalente, aumentata di 5.

Nello studio della relazione dose-risposta, la percentuale di individui che rispondono all'effetto causato della dose viene di solito rappresentato con una curva cumulata. Essa ha forma sigmoide, se la curva della distribuzione originaria è normale, con la conseguenza che a parità di errore nella dose l’errore nella risposta non è costante, ma varia secondo il punto in cui incontra perpendicolarmente la sigmoide. Per un errore costante nella risposta, occorre trasformarla in una retta.

 

La curva percentuale cumulata può essere linearizzata in vari modi. Uno dei più diffusi consiste appunto nei probits, ottenuti con due passaggi logici:

1- Sostituire ai valori di p dell'ordinata quelli corrispondenti all'ascissa della distribuzione normale standardizzata

 

 

A causa della simmetria della distribuzione normale, il 50% dei valori Y' è negativo e l'altro 50% è positivo. E' noto e può anche essere osservato sulla tabella della distribuzione normale che meno di 2 valori su 10.000 hanno un valore di inferiore a -3,5.

2 - Successivamente a tutti i valori trasformati in Y' aggiungere la quantità 5: si eliminano tutti i valori negativi.

Questi valori trasformati mediante la relazione

 sono i probits.

 

Nei suoi effetti, questa trasformazione è analoga a quella angolare, in quanto i valori verso gli estremi della distribuzione sono più dilatati di quelli collocati nella parte centrale. Il campo di variazione della scala probit tende all'infinito; la scala dei probit si distingue da quella angolare soprattutto nei valori prossimi a 0 e a 1. La trasformazione in probits, rendendo lineare la sigmoide di una cumulata tratta dalla distribuzione normale, permette di trattare la stima dei parametri della distribuzione normale (m e s) come quello dei parametri di una regressione lineare (intercetta a e coefficiente angolare b). Ma la stima corretta dei parametri della retta richiede che i punti sperimentali abbiano la stessa varianza; di conseguenza i valori dei probits dovrebbero essere ponderati.

L’effetto linearizzante della trasformazione probit è stato ampiamente utilizzato nelle carte di probabilità, usate per verificare in modo semplice e con un grafico se una distribuzione era normale. La diffusione dei calcolatori, che permettono stime rapide ed esatte dei valori di asimmetria e curtosi di una serie di dati campionari, ha reso superflui questi metodi grafici.

 

La trasformazione normit

è un’altra trasformazione di percentuali cumulative basate sull’integrale di probabilità della curva normale. Fornisce valori diversi dai probits.

 

La trasformazione logit viene anche essa applicata a osservazioni percentuali ed è ottenuta con

L'effetto di questa trasformazione logistica o logit è simile a quella probit e può determinare analisi del tutto uguali, in particolare nello studio del dosaggio con risposte quantali.

L'attuale diffusione dell'informatica, che ha superato le difficoltà derivanti dalla complessità dei calcoli e dal tempo richiesto nei calcoli manuali, ha annullato la necessità di linearizzare le distribuzioni. Di conseguenza, le trasformazioni probit e logit sono sempre meno usate.