trasformazionI dei dati;

test per normalita’ e PER OUTLIER

 

 

13.10.  IDENTIFICAZIONE DEGLI OUTLIER CON IL METODI GRAFICI: IL Box-and-Whiskers DI TUKEY.

 

 

Tra questi metodi grafici già riportati nel capitolo I sulla statistica descrittiva, quali gli stem-and-leaf plots e gli istogrammi, il più diffuso è il diagramma a scatola (box-plot), chiamato anche diagramma a scatola e baffi (Box-and-Whiskers), presentato in modo organico da John W. Tukey nel suo testo del 1977 Exploratory Data Analysis (pubblicato da Addison-Wesley, Reading, Mass.).

Serve per rappresentare visivamente le tre caratteristiche fondamentali di una distribuzione statistica:

- il grado di dispersione o variabilità dei dati, rispetto alla mediana e ai quartili;

- la simmetria;

- la presenza di valori anomali.

 

La preferenza attribuita a questo metodo rispetto agli altri metodi grafici deriva dal fatto che con gli altri metodi l’identificazione di una osservazione anomala è basata soltanto sul nostro occhio, mentre nel caso dei diagrammi a scatola le osservazioni anomale sono definite su base statistica: questo può aiutarci a beccare anche quelle che altrimenti l’avrebbero passata liscia. Dunque i diagrammi a scatola combinano la ricerca visiva degli anomali con un po’ di statistica (ancora Geoff R. Norman e David L. Streiner a pag. 203).

 

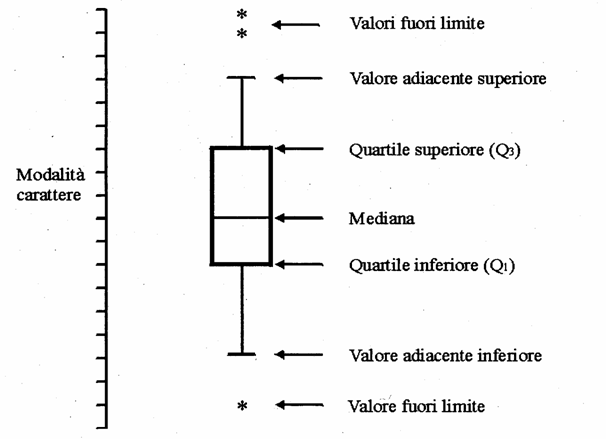
Anche se la serie di concetti implicati è lunga, partendo dal centro nella figura successiva è semplice osservare che

 

1 -  la linea interna alla scatola (box) rappresenta la mediana;

 

2 -  mentre le due linee orizzontali rappresentano i bordi della scatola e identificano

- il primo quartile (Q₁, nella parte inferiore o Q lower) e

- il terzo quartile (Q₃, nella parte superior o Q upper);

 di conseguenza, entro esse è compreso il 50 % delle osservazioni, quelle “più normali”, collocate nella parte centrale della distribuzione.

 

3 -  La distanza  tra i due quartili (), chiamata distanza interquartile, è assunta come misura di riferimento per valutare e testare la variabilità dei dati.

 

4 - A partire dai bordi della scatola, si allungano due linee verticali o baffi (whiskers) di lunghezza uguale (o minore) a 1,5 (chiamato step da Tukey) e che terminano con un tratto orizzontale:

- la linea che parte dal quartile inferiore Q₁ e si prolunga verso il basso è il Valore Adiacente Inferiore (in italiano VAI; in inglese lower fence);

- quella che parte dal quartile superiore Q₃ e si prolunga verso l’alto è il Valore Adiacente Superiore (in italiano VAS, in inglese upper fence).

 

 

 

5 - In particolare quando le osservazioni sono poche, i due valori limiti che distano dal quartile 1,5 (uno step), non coincidono con nessun dato; di conseguenza, come nel caso della figura riportata, al loro posto per ognuno dei due baffi è stato preso quello più vicino, che è compreso nella parte interna della distribuzione.

 

6 -  Il valore adiacente inferiore VAI è il più piccolo dei valori osservati che risultano maggiori o uguali al limite prima prefissato;

 

7 - mentre il valore adiacente superiore VAS è il più grande dei valori osservati che risultano minori o uguali al limite prima prefissato.

 

8 - Ne deriva che le due linee verticali, come nel grafico, quando sono calcolate su dati reali possono avere lunghezza inferiore a 1,5e diversa per i due baffi; essi individuano un confine detto cinta interna (inner fence).

 

9 - I dati esterni a questa cinta sono rappresentati individualmente (perché quasi sempre sono pochi) e negli output informatici di norma sono indicati con un asterisco (come nella figura riportata): sono gli outlier o valori anomali detti anche valori fuori limite.

 

10 – Seppure senza la presenza di alcun tratto grafico e quindi non visibile,

-   nel disegno è presente un ulteriore confine, più esterno,

-   detto cinta esterna  (outer fence) e che dista 2 step (3) dal quartile di riferimento:

 esso delimita un ultimo limite, oltre il quale gli outlier da anomali diventano estremamente anomali;

 

Molti pacchetti informatici che disegnano il box plot, distinguono queste due categorie di outlier utilizzando simboli differenti per i punti vicini e quelli lontani. Ad esempio, nelle versioni in commercio nell’anno 2000,

- SPSS/PC usa O per gli outlier vicini e E per gli outlier estremi,

- Minitab usa un * (asterisco) per gli outlier vicini e una O per gli outlier estremi.

 

Spesso il disegno è riportato in modo verticale, come nella figura precedente. I concetti sono del tutto identici quando la rappresentazione è orizzontale; ma a molti il primo modo appare di più facile lettura, in particolare quando si confrontano due distribuzioni.

 

 Da questa presentazione del box-whisker plot, si evidenzia che le due misure fondamentali che permettono di individuare singolarmente tutti gli outlier di una distribuzione di dati sono

-  la distanza interquartile ()

-  e la scelta della lunghezza dei due tratti, che come valore unitario ha 1,5.

Ma mentre il valore  è oggettivo e dipende dalla dispersione dei dati, il coefficiente 1,5 è soggettivo. Alla domanda perché avesse fissato una distanza di 1,5 e non un altro coefficiente, John Tukey rispose:” Perché 1 è  poco e 2 è troppo”.

Si ritorna quindi alla soggettività nei criteri di individuazione degli outlier, anche se fondati sulla esperienza e competenza di uno statistico come John Tukey (1915 - 2000), nato nel Massachusettes, fondatore del Dipartimento di Statistica di Princeton, con contributi fondamentali sulle time series, il concetto di robustezza di un test, l’analisi della varianza, i confronti multipli e inventore della exploratory data analysis, entro la quale è da collocare questo metodo grafico.

 

A questo grafico è imputato il limite di non essere fondato direttamente sulla stima di una probabilità precisa per ogni valore.

E’ tuttavia importante sottolinearne il concetto di base: se i dati sono distribuiti in modo normale, approssimativamente perché quasi sempre sono pochi,

-  oltre la cinta interna  cade complessivamente il 5% delle osservazioni,

- oltre la cinta esterna l’1% delle osservazioni più estreme.

 

 

ESEMPIO 1.  Si supponga di avere raccolto la seguente serie di 20 valori, in una scala di rapporti  o ad intervalli:

61,  69,  28,  51,  112,  80,  73,  103,  40,  47,  58,  58,  74,  56,  64,  68,  56,  54,  63,  59

Organizzare i valori in modo da costruire il box-plot e individuare gli eventuali outlier.

 

Risposta. Dopo aver ordinato le osservazioni per rango,

28,  40,  47,  51, 54,  56, 56,  58,  58,  60,  60,  63,  64,  68,  69,  73,  74,  80,  103,  112

 con 20 dati

-  la mediana è tra i valori di rango 10 (60) e di rango 11 (60): mediana = 60

-  il quartile inferiore cade tra i valori di rango 5 (54) e rango 6 (56): Q₁ = 55

-  il quartile superiore cade tra i valori di rango 15 (69) e rango 16 (73): Q₃ = 71

- la distanza interquartile è : = 71 – 55 = 16

-  il valore adiacente inferiore (VAI) è il più piccolo dei valori osservati che risultano maggiori o uguale al limite ottenuto con

 = 55 – (1,5 = 55 – 24 = 31

 ma poiché nessun valore è uguale a 31 e quello minore tra i maggiori di 31 è 40: VAI = 40

-  il valore adiacente superiore (VAS) è il più grande dei valori osservati che risultano minori o uguali al limite ottenuto con

 = 71 + (1,5 = 71 + 24 = 95

 ma poiché nessun valore è uguale a 31 e quello maggiore tra i minori di 95 è 80: VAS = 80

 

Da queste due ultime indicazioni si ricavano gli outlier:

-  nella parte inferiore è 28, in quanto inferiore a 40;

- nella parte superiore sono outlier 103 e 112, in quanto superiori a 80

 

Se si rappresentano graficamente questi dati, si ottiene una figura molto simile a quella riportata in precedenza.

Non esiste alcun outlier estremo. Infatti

-  per il valore minimo la cinta esterna è

 = 55 – (3 = 55 – 48 = 7

 uguale a 7, mentre il minimo del campione è 28

-  per il valore massimo la cinta esterna è

 = 71 + (3 = 71 + 48 = 119

uguale a 119, mentre il massimo del campione è 112.