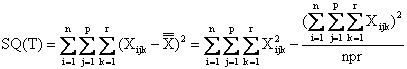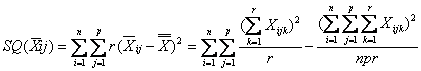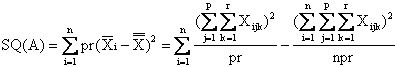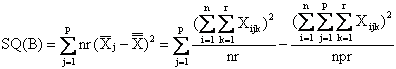analisi FATTORIALE E  disegni complessi

CON FATTORI INCROCIATI

 

 

 

12.2.   INTERAZIONE TRA DUE FATTORI A PIU’ LIVELLI

 

 

Per il rapido incremento della complessità dell’analisi all’aumentare del numero di fattori, lo studio dell’interazione è qui limitato ai casi più semplici. Come già avvenuto per vari altri argomenti e come sarà ripetuto anche in altri casi dei capitoli successivi, per analisi più complesse che superano le finalità di questo corso elementare si rinvia a trattazioni specifiche.

Con due fattori e con dati riportati in una tabella a due entrate, secondo le modalità già presentate nel caso di esperimenti a blocchi randomizzati, è possibile analizzare l’interazione solo quando si dispone di più osservazioni in ognuna delle celle poste all'incrocio tra righe e colonne.

 

Il modello additivo dell'ANOVA diventa

 

dove:

-   è la media generale che, riferita ai dati dell’esperimento, è stimata nel modo migliore mediante la media campionaria di tutti i dati

-   è l'effetto del trattamento i che, con i dati campionari, può essere calcolato come differenza della sua media dalla media generale:

 

-   è l'effetto del blocco j che, nell’esperimento, è determinato dalla differenza della sua media dalla media generale:

 

-  è l'interazione tra l'effetto  del trattamento i e l'effetto  del trattamento j; con dati sperimentali, può essere misurata come somma dei quadrati delle differenze tra la media osservata e quella attesa entro ogni casella

 

 dove

-  è la media attesa e può essere calcolata sommando alla media generale l'effetto-riga e l'effetto-colonna alla quale la casella appartiene:

 

-  è la differenza tra una singola osservazione e la sua media di casella:

 

La devianza totale, quella tra trattamenti e quella tra blocchi sono calcolate con le stesse modalità già spiegate nel capitolo precedente.

 

La devianza d’interazione  secondo la formula euristica è la somma dei quadrati degli scarti tra media osservata e media stimata in ogni casella

 

  = 

 

 mentre la devianza entro od errore  è la somma dei quadrati degli scarti di ogni replica dalla sua media di casella

 

Di conseguenza, nel modello ANOVA a due fattori con replicazioni, la devianza totale può essere suddivisa in 4 devianze:

- devianza del fattore  ;

- devianza del fattore  ;

- devianza dovuta all'effetto dell'interazione  ;

- devianza d'errore o residuo.

 

 

Esse ed i loro gdl godono della proprietà additiva

 

 

che permette di verificare i calcoli oppure di stimare una di esse a partire dalle altre quattro.

In questo modello, di norma i dati sono riportati in una tabella secondo lo schema generale successivo. In esso,

- i trattamenti sono indicati in colonna,

- i blocchi sono indicati nelle righe,

- le repliche sono riportate nelle caselle, all’incrocio tra trattamenti e righe:

 

 

 

 

 

 e dove

-    è il valore della k-esima osservazione nel livello i-esimo del fattore A (trattamento) e nel livello j-esimo del fattore B (blocco),

-   sono rispettivamente la somma e la media dei valori (repliche) della casella, collocata all'incrocio tra il trattamento i-esimo ed il blocco j-esimo,

 ed inoltre, con la simbologia consueta,

-   sono la somma e la media dei valori per la colonna i del fattore A (trattamenti),

-   sono la somma e la media dei valori per la riga j del fattore B (blocchi),

-   sono la somma  e la media generale.

 

Per valutare la significatività delle differenze tra i vari livelli del fattore A e del fattore B oltre a quella dell'interazione AB, il test F dell'analisi della varianza richiede il calcolo delle quantità riportate nella tabella sottostante, con i relativi gdl:

 

 

 

 

- dove,

- n è il numero di livelli del fattore A;

- p è il numero di livelli del fattore B;

- r è il numero di repliche entro ogni casella.

 

Come per la devianza totale,

la devianza tra le medie di casella o devianza di tutti i fattori non è utile al calcolo dei test F; essa ha solo il duplice scopo di

- essere didatticamente utile per comprendere più compiutamente il significato delle altre devianze e

- soprattutto di permettere calcoli più semplici per ottenere la devianza d'interazione, mediante una semplice differenza con le devianze già note dei fattori A e B analizzati in modo separato.

 

La devianza totale SQ(T), definita come la somma dei quadrati degli scarti di ogni dato rispetto alla media generale, con la formula abbreviata può essere calcolata come differenza tra la somma dei quadrati di ogni dato ed il quadrato della somma generale diviso il numero totale di dati (chiamato anche termine di correzione):

Il numero di gdl della devianza totale è uguale al numero totale di dati od osservazioni meno uno (npr-1).

 

La devianza tra le medie delle caselle o devianza dei fattori, indicata con , per definizione è la somma dei quadrati degli scarti di ogni media di casella dalla media generale, moltiplicata per il numero di dati entro ogni casella; per comprendere il significato della formula, è utile ricordare che, se esistesse solamente la variabilità tra le caselle, tutte le repliche entro ogni casella avrebbero lo stesso valore. Con la formula abbreviata, questa devianza può essere calcolata per differenza tra la somma dei quadrati delle somme dei dati entro ogni casella diviso il numero di repliche e tra il quadrato della somma generale diviso il numero totale di dati (termine di correzione):

 

Il numero di gdl della devianza tra le medie di ogni casella è uguale al numero di caselle meno uno, corrispondente a  (np-1).

 

La devianza tra trattamenti o del fattore A, indicata con SQ(A), è la somma dei quadrati degli scarti tra la media di ogni trattamento e la media generale, moltiplicata per il numero di dati del trattamento; infatti se la variabilità fosse determinata solamente dagli effetti del trattamento, tutti i dati dello stesso trattamento dovrebbero essere tra loro uguali. Con la formula abbreviata, la devianza tra trattamenti può essere calcolata per differenza tra la somma dei quadrati della somma di ogni trattamento, diviso il numero di dati del trattamento, e tra il quadrato della somma generale diviso il numero totale di dati (termine di correzione):

 

 

 

La devianza tra blocchi o del fattore B, indicata con SQ(B) è la somma dei quadrati degli scarti tra la media di ogni blocco e la media generale, moltiplicata per il numero di dati del blocco: se la variabilità tra le osservazioni fosse determinata solamente dall'effetto del blocco, tutti i dati dello stesso blocco dovrebbero avere lo stesso valore. Con la formula abbreviata, la devianza tra blocchi può essere calcolata per differenza tra la somma dei quadrati delle somme di ogni blocco, divisa per il numero di dati del blocco, e tra il quadrato della somma generale diviso il numero totale di dati (termine di correzione):

 

La devianza d'interazione tra i fattori A e B, indicata con SQ(AB), è la somma dei quadrati degli scarti di ogni media di casella rispetto al valore atteso dall'effetto trattamento e dall'effetto blocco ritenuti additivi

 

In modo molto più semplice e veloce, la devianza d'interazione e i suoi gdl sono misurati per sottrazione dalla devianza tra le medie delle devianze sia del fattore A che del fattore B:

 

 

La devianza d'errore o residuo, indicata con SQ(e), per definizione è la somma dei quadrati degli scarti di ogni valore rispetto alla media della sua casella:

 

 

Con r dati entro ogni casella, i suoi gdl sono    .

Più rapidamente, la devianza d'errore è ottenuta sottraendo dalla devianza totale la devianza tra le medie delle caselle:

 

Dividendo la devianza tra trattamenti, quella tra blocchi, quella d'interazione e quella d'errore per i rispettivi gdl si ottengono le varianze corrispondenti:

 

;           ;           ;         

 

Nel modello ANOVA a due fattori con repliche, si possono verificare 3 ipotesi distinte ed eseguire i tre test corrispondenti.

 

1 - Si verifica l'ipotesi nulla di nessuna differenza tra le medie del fattore A:

contro l'ipotesi alternativa:

 

mediante il test F, con gdl n-1 al numeratore e np(r-1) al denominatore,

 dove l'ipotesi nulla viene respinta se il rapporto supera il valore critico alla significatività a prescelta.

 

2 - Si verifica l'ipotesi nulla di nessuna differenza tra le medie del fattore B

contro l'ipotesi alternativa

H₁: non tutte le m sono tra loro uguali

mediante il test F con gdl p-1 al numeratore e np(r-1) al denominatore

dove l'ipotesi nulla viene respinta se il rapporto supera il valore critico alla significatività prescelta.

 

3 - Si verifica l'ipotesi nulla di nessuna interazione tra i fattori A e B ai vari livelli

 

H₀: AB_ij = 0 per ogni i e j

contro l'ipotesi alternativa

H₁: AB_ij ¹ 0 per almeno un  ij

mediante il ricorso ad un test F con gdl

-          (n-1)(p-1) al numeratore 

-            np(r-1) al denominatore

 e si respinge l'ipotesi nulla se il rapporto supera il valore critico alla probabilità a prefissata.

 

ESEMPIO.  Si vuole verificare se insetti adulti della stessa specie che vivono in 4 località differenti (A, B, C, D) hanno differenze significative nelle loro dimensioni, considerando pure che dalla primavera all'autunno continuano ad aumentare.

 

 

In altri termini, ci si chiede se la crescita è diversa nelle 4 località in rapporto alle stagioni (per semplificare al massimo i calcoli, sono state riportate solamente 2 misure per località e stagione).

 

Risposta. E’ un’analisi a due fattori con repliche, con analisi dell’interazione tra località e stagioni. Dapprima si devono stimare i totali e le medie, necessari per i calcoli successivi

 

 

- La devianza totale , con 23 gdl (per tutti e 24 i dati) è ottenuta con

 e corrisponde a :

 

- La devianza tra le medie delle caselle o dei vari livelli dei due fattori, con 11 gdl (le medie delle caselle all’incrocio località per stagione sono 12) è data da

 

e corrisponde a (con i totali delle 12 caselle)

 

- La devianza tra trattamenti o del fattore A, con 3 gdl è calcolata (per le 4 medie di colonna) da

 

ed è uguale a (con i totali dei 4 trattamenti):

 

- La devianza tra blocchi o del fattore B, con 2 gdl è ottenuta mediante

 

e corrisponde a (con i totali dei 3 blocchi)

 

- La devianza d'interazione AB viene stimata per differenza:

e nello stesso modo vengono calcolati i rispettivi gdl

 

- La devianza d'errore o residuo nei calcoli manuali viene quasi sempre stimata per differenza

e nello stesso modo sono calcolati i suoi gdl

I gdl della devianza d'errore possono essere calcolati anche in modo diretto: ognuna delle 12 caselle con 2 dati contribuisce alla devianza d'errore complessiva con 1 gdl, fornendo un totale di 12 gdl.

 

E' utile disporre le devianze e i gdl in tabella, con il calcolo delle 4 varianze utili ai 3 test F:

 

 

 

 

Per le differenze tra trattamenti o effetto del fattore A si calcola un test F con gdl 3 e 12

 il cui valore critico alla probabilità a = 0.05 è uguale a 3,49.

 

Per le differenze tra blocchi o effetto del fattore B si calcola un test F con gdl 2 e 12

 il valore critico del quale alla probabilità a =  0.05 è 3,89.

 

Per l'effetto dell'interazione AB si calcola un test F con gdl 6 e 12

 che fornisce un rapporto inferiore ad 1 e

 quindi non è significativo.

 

Con i risultati dell'esempio, si possono trarre le conclusioni relative ai tre test F:

1 - nelle 4 località, le dimensioni medie degli insetti sono significativamente differenti;

2 - tra primavera, estate ed autunno le dimensioni medie degli insetti variano significativamente;

3 - non esiste interazione: nelle 4 località le dimensioni medie degli insetti variano con intensità simile durante le stagioni.

 

Il disegno sperimentale dell’analisi della varianza a più criteri è la vera novità introdotta da Fisher; su di essa si fonda la statistica moderna. Con l'assunzione che la natura risponde solamente a domande semplici, si era diffuso tra i ricercatori un metodo d'indagine che imponeva la variazione di un solo fattore sperimentale alla volta. Fisher dimostrò il vantaggio del disegno sperimentale di tipo fattoriale: se si seguono contemporaneamente più fattori, si riesce ad evidenziare le loro interazioni e si ha una visione più corretta della complessità delle risposte. Si ottengono anche i vantaggi di poter utilizzare un numero minore di osservazioni e di ridurre sensibilmente la varianza d'errore.

 

Gli esperimenti fattoriali per l’analisi dell’interazione tra 2 fattori a vari livelli sono condotti in laboratorio altrettanto spesso che nelle ricerche di campagna. Per chi non ha esperienza, l’approccio metodologico utilizzato in laboratorio appare diverso da quello impiegato in campagna, poiché i risultati spesso sono presentati in tante colonne, quante sono le combinazioni dei livelli dei due fattori a confronto, come se si trattasse di un’analisi ad un criterio di classificazione.

 

Con il fattore A a tre livelli (a₁, a₂, a₃) ed il fattore B a due modalità (b₁ e b₂) si devono formare 6 gruppi, date dalle loro combinazioni, ognuno con lo stesso numero d’osservazioni. Di norma i risultati sono riportati in una tabella che solo apparentemente è ad una sola entrata.

 

 

 

 

E’ sufficiente una corretta impostazione tabellare come quella sottostante

 

 

per rendere evidente che si tratta di un esperimento a due fattori con repliche.

E’ quindi un esperimento fattoriale, con il quale è possibile analizzare contemporaneamente se esiste differenza tra le varie modalità entro ognuno dei due fattori e se l’interazione tra loro è significativa.

 

ESEMPIO.   Si vogliono verificare gli effetti di 3 mangimi industriali, contenenti ormoni sintetici, sulla crescita di animali: un aspetto fondamentale della ricerca è dimostrare se nei due sessi hanno un effetto di segno opposto.

A questo scopo, i 3 tipi di mangime (,,) sono stati somministrati 

- a tre gruppi di femmine (),  formati ognuno da 5 individui scelti per estrazione casuale da un grande gruppo di femmine, e

- a tre gruppi di maschi (), formati ognuno da 5 individui scelti per estrazione casuale da un grande gruppo di soli maschi.

 

Dopo un mese di dieta, è stato misurato l’accrescimento di ogni cavia.

Per ognuno dei  gruppi, i risultati sono riportati nella tabella sottostante:

 

 

Esiste interazione tra farmaci e sesso?

 

Risposta. Se non già fatto nella presentazione dei risultati, soprattutto per l’apprendimento dei metodi risulta utile impostare i dati secondo una tabella che evidenzi che si tratta di un’analisi a due fattori con repliche, non di un’ANOVA ad un solo criterio di classificazione:

 

 

Nel passaggio successivo, da essa è utile ricavare una nuova tabella con tutte le medie da analizzare:

 

 

Con questi dati riassuntivi, è più semplice formulare le tre ipotesi alle quali il test permette di rispondere.

1) La prima è relativa alle medie dei tre mangimi (a₁ , a₂ , a₃) con ipotesi nulla

H₀ :  m_a1 = m_a2 = m_a3

ed ipotesi alternativa H₁ che le m dei tre farmaci non sono tutte uguali.

 

2) La seconda ipotesi nulla è relativa alla media dei sessi (b₁ e b₂)

H₀ :  m_b1 = m_b2

con ipotesi alternativa bilaterale

H₁ :  m_a1 ¹ m_a2

 

3) La terza ipotesi riguarda la significatività dell’interazione tra il fattore A e il fattore B, con ipotesi nulla

H₀ :  ab = 0

che afferma che non esiste interazione

ed ipotesi alternativa

H₁:  ab ¹ 0

che afferma che l’interazione è significativa, pure senza specificarne la direzione.

 

Per rispondere a questi quesiti, si deve utilizzare lo stesso schema dell'analisi a due criteri di classificazione con misure ripetute; pertanto si devono calcolare:

 

1 - la devianza totale che è fondata sugli scarti di ogni valore dalla media generale (23,1); con 30 dati, i gdl sono 29;

 

2 - la devianza tra le medie di casella o delle combinazioni tra i due fattori, che è fondata sugli scarti di ognuna delle 6 medie (20,0;  24,6;  16,0;  31,4;  28,6;  18,4) dalla media generale; i gdl sono 5;

 

3 - la devianza dovuta al fattore A, tra le medie dei 3 tipi di mangime (25,7;  26,6;  17,2) con 2 gdl;

 

4 - la devianza dovuta al fattore B,  tra le medie dei 2 sessi (20,200;  26,133), con 1 gdl;

 

5 - la devianza d'interazione AB, mangime per sesso, ottenuta facilmente per sottrazione della devianza del fattore A più quella del fattore B dalla devianza tra le medie di casella; nello stesso modo si stimano i gdl; questa devianza stima se le sei medie di casella sono determinate dalla somma degli effetti di riga e di colonna o se risentono in modo significativo dell’interazione;

 

6 - la devianza d'errore o residuo, data dagli scarti di ognuna delle 30 osservazioni dalla loro media di gruppo; con 5 dati, ogni gruppo contribuisce con 4 gdl per un totale di 24 gdl (4 x 6); più rapidamente, la devianza d'errore ed i suoi gdl sono ottenuti per sottrazione della devianza tra le medie di casella dalla devianza totale.

 

Con le formule già presentate, si calcolano le devianze, i gdl e le varianze

 

 

 utili ai 3 test F.

Per il fattore A

 

 si ottiene un F con gdl 2 e 24 uguale a 30,74

 mentre il valore critico alla probabilità a = 0.05 è uguale a 3,40.

Per il fattore B,

 

 si ottiene un F con gdl 1 e 24 uguale a 30,17

 che deve essere confrontato con un valore critico alla probabilità a =  0.05 uguale a 4,26.

Per l'interazione A x B,

 

 il valore di F con gdl 2 e 24 è uguale a 6,57

 mentre il suo valore critico alla probabilità a = 0.05 è uguale a 3,40.

Dal confronto dei tre valori di F con i rispettivi valori critici, si possono trarre

 le conclusioni relative alle tre ipotesi nulle:

1 - i tre mangimi danno medie di accrescimento significativamente differenti;

2 - i due sessi hanno accrescimenti significativamente differenti;

3 - l'interazione tra i due fattori (mangime e sesso) è significativo, presumibilmente per la presenza di ormoni sintetici.