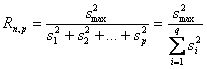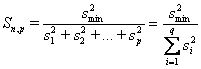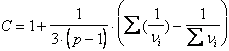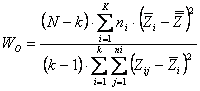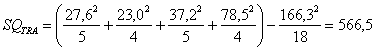10.3.   TEST per l'omogeneitA' dellA varianzA TRA PIu’ CAMPIONI:  TEST DI HARTLEY,  COCHRAN,  BARTLETT,  LEVENE E LEVENE MODIFICATO DI BROWN-FORSYTHE

 

 

Il confronto tra medie con l'analisi della varianza richiede che i diversi gruppi abbiano varianze uguali. Allontanarsi sensibilmente da questa condizione di validità influenza gravemente la varianza d’errore, quindi la significatività del test. Si utilizzerebbe una varianza d'errore media s², come stima della varianza vera s², che risulterebbe troppo grande per alcuni trattamenti e troppo piccola per altri.

Oltre alla verifica delle condizioni di validità per il confronto tra medie, spesso si ha anche un interesse esplicito a un confronto tra le varianze. Per esempio,

-  gruppi di animali o piante geneticamente identici dovrebbero avere varianze significativamente minori di gruppi geneticamente eterogenei;

-  gruppi di animali oppure di vegetali cresciuti in condizioni ambientali molto differenti dovrebbero avere una varianza maggiore di gruppi allevati in condizioni simili;

-  nelle analisi di laboratorio, uno strumento di misura più preciso od un reagente di qualità superiore dovrebbero fornire varianze minori rispetto a strumenti e reagenti di bassa qualità, in esperimenti ripetuti nelle stesse condizioni.

 

L'ipotesi di omoscedasticità, chiamata in alcuni testi in italiano anche omoscedalità oppure omogeneità delle varianze, nel caso di più gruppi richiede la verifica dell'ipotesi nulla

 

contro l'ipotesi alternativa

 

I termini sono derivati direttamente da homoscedasticity usato come sinonimo di omogeneità delle varianze e heteroscedasticity sinonimo di eterogeneità delle varianze, introdotte da Karl Pearson nel 1905.

I metodi proposti sono numerosi; tra i più diffusi, di norma utilizzati anche nei programmi informatici standard per calcolatori, sono da ricordare

A - il test F_max di Hartley,

B - il test della varianza massima o della varianza minima di Cochran,

C - il test di Bartlett,

D – il test di Levene.

 

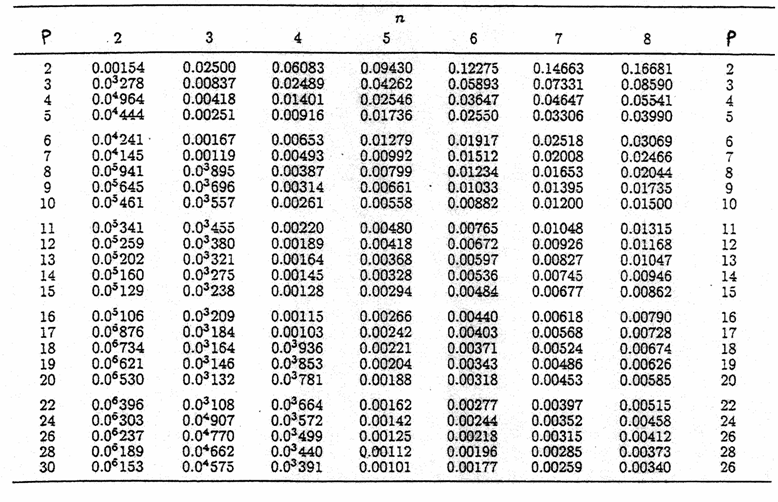
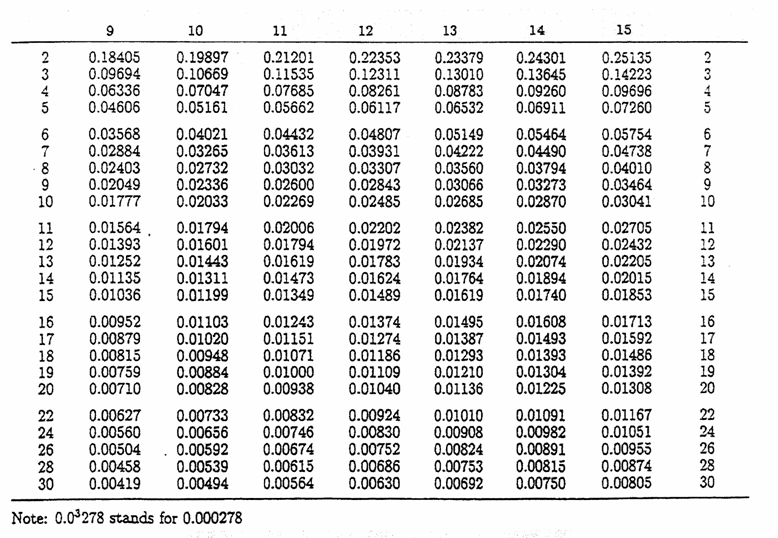
A) Il procedimento F_max di Hartley è quello più semplice e rapido, come generalizzazione del test per due campioni indipendenti. Le difficoltà alla sua utilizzazione derivano solo dalla scarsa reperibilità di testi ad ampia diffusione che riportino la tabella dei valori critici. Questa tabella (riportata nella pagina successiva) non è da confondere con quella di Fisher-Snedecor, presente in tutti i testi. Esse coincidono solo nel caso di due campioni indipendenti

Tale difficoltà a reperire le tabelle è ora superata in molti programmi informatici recenti, che insieme con il valore dell’indice di omoscedasticità riportano anche la sua probabilità P.

 

Secondo il test di Hartley, esiste una differenza significativa tra più varianze quando il rapporto tra la varianza maggiore s²_max     e la varianza minore s²_min

 

 

 supera il valore critico riportato nelle tabelle corrispondenti.

Gli indici dei valori di F_max  considerano il numero p di gruppi a confronto simultaneo ed il numero di gradi di libertà n-1 di ogni gruppo.

Il test richiede che i gruppi abbiano tutti lo stesso numero n di osservazioni.

 

E' un test semplice, ma non robusto: l'assunzione fondamentale è che i dati siano distribuiti normalmente. Se non è possibile supporre la normalità della distribuzione per ciascun gruppo, si dovrebbe ricorrere ad altri test, come quelli non parametrici.

Infatti

-  non esistono test parametrici adatti alla verifica della omogeneità della varianza,

-  quando le distribuzioni dei dati si discostano dalla normalità.

 

 

B) Anche il test proposto da Cochran nel 1967 può essere applicato solo ad esperimenti bilanciati. E' metodologicamente

-  semplice come il precedente e

-  permette una verifica rapida dell'ipotesi nulla di omoscedasticità dei vari trattamenti.

I metodi di Cochran sono due, tra loro alternativi:

-  il test della varianza massima,

-  il test della varianza minima

 

Valori critici per il test di Hartley

sull’omogeneità della varianza tra k gruppi

 

a = 0.05

 

Numero k di varianze a confronto

 

Df2	2	3	4	5	6	7	8	9	10	1l	12
2	39.0	87.5	142	202	266	333	403	475	550	626	704
3	15.4	27.8	39.2	60.7	62.0	72.9	83.5	93.9	104	114	124
4	9.60	15.5	20.6	26.2	29.5	33.6	37.5	41.1	44.6	48.0	51.4
5	7.15	10.3	13.7	16.3	18.7	20.8	22.9	24.7	26.5	28.2	29.9
6	5.82	8.38	10.4	12.1	13.7	15.0	16.3	17.5	18.6	19.7	20.7
7	4.99	6.94	8.44	9.70	10.8	11.8	12.7	13.5	14.3	15.1	15.8
8	4.43	6.00	7.18	8.12	9.03	9.78	10.5	11.1	11.7	12.2	12.7
9	4.03	5.34	6.31	7.11	7.80	8.41	8.95	9.45	9.91	10.3	10.7
10	3.72	4.85	5.67	6.34	6.92	7.42	7.87	8.28	8.66	9.01	9.34
12	3.28	4.16	4.79	5.30	5.72	6.09	6.42	6.72	7.00	7.25	7.48
15	2.86	3.54	4.01	4.37	4.68	4.95	5.19	5.40	5.59	5.77	5.93
20	2.46	2.95	3.29	3.54	3.76	3.94	4.10	4.24	4.37	4.49	4.59
30	2.07	2.40	2.61	2.78	2.91	3.02	3.12	3.21	3.29	3.36	3.39
60	1.67	1.85	1.96	2.04	2.11	2.17	2.22	2.26	2.30	2.33	2.36
¥	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00

 

 

a = 0.01

 

Numero k di varianze a confronto

 

Df2	2	3	4	5	6	7	8	9	10	11	12
2	199	448	729	1036	1362	1705	2063	2432	2813	3204	3605
3	47.5	85	120	151	184	216	249	281	310	337	361
4	23.2	37	49	59	69	79	89	97	106	113	120
5	14.9	22	28	33	38	42	46	50	54	57	60
6	11.1	15.5	19.1	22	25	27	30	32	34	36	37
7	8.89	12.1	14.5	16.5	18.4	20	22	23	24	26	27
8	7.50	9.9	11.7	13.2	14.5	15.8	16.9	17.9	18.9	19.8	21
9	6.54	8.5	9.9	11.1	12.1	13.1	13.9	14.7	15.3	16.0	16.6
10	5.85	7.4	8.6	9.6	10.4	11.1	11.8	12.4	12.9	13.4	13.9
12	4.91	6.1	6.9	7.6	8.2	8.7	9.1	9.5	9.9	10.2	10.6
15	4.07	4.9	5.5	6.0	6.4	6.7	7.1	7.3	7.5	7.8	8.0
20	3.32	3.8	4.3	4.6	4.9	5.1	5.3	5.5	5.6	5.8	5.9
30	2.63	3.0	3.3	3.4	3.6	3.7	3.8	3.9	4.0	4.1	4.2
60	1.96	2.2	2.3	2.4	2.4	2.5	2.5	2.6	2.6	2.7	2.7
¥	1.00	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0

 

 

Il test della varianza massima è quello originario proposto da Cochran.

E’ fondato sul rapporto tra la varianza massima e la somma di tutte le altre varianze.

Si calcola il valore del rapporto

 dove

-  la varianza campionaria maggiore,

-    sono le varianze dei p gruppi,

 con un numero n di repliche uguali in ogni gruppo.

 

Anche in questo caso, i limiti derivano dall’esigenza di un numero uguale di osservazioni in tutti i gruppi e dalla ridotta diffusione delle tabelle specifiche. Con un numero di osservazioni molto alto (infinito) il rapporto tende a 1/p.

 

Il test della varianza minima è data dal rapporto tra la varianza minima e la somma di tutte le altre varianze.

Si calcola il valore del rapporto

 dove

-  la varianza campionaria minore,

-    sono le varianze dei p gruppi,

 con un numero n di repliche uguali in ogni gruppo.

Validità e limiti sono del tutto identici al test della varianza massima.

 

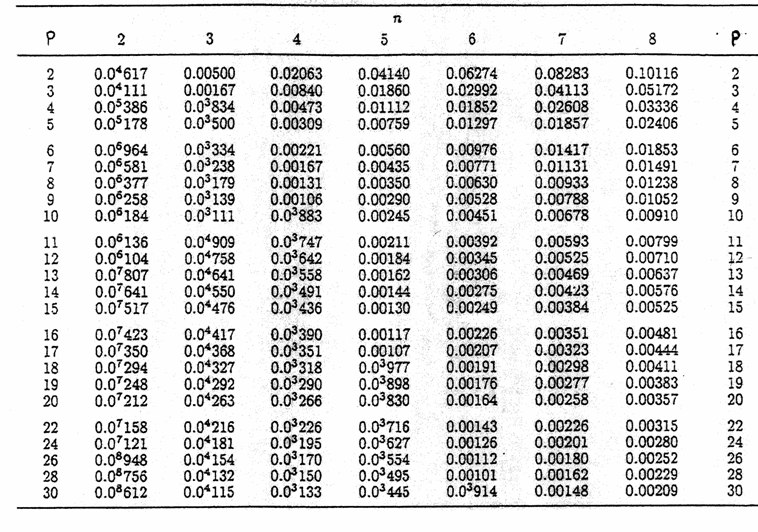
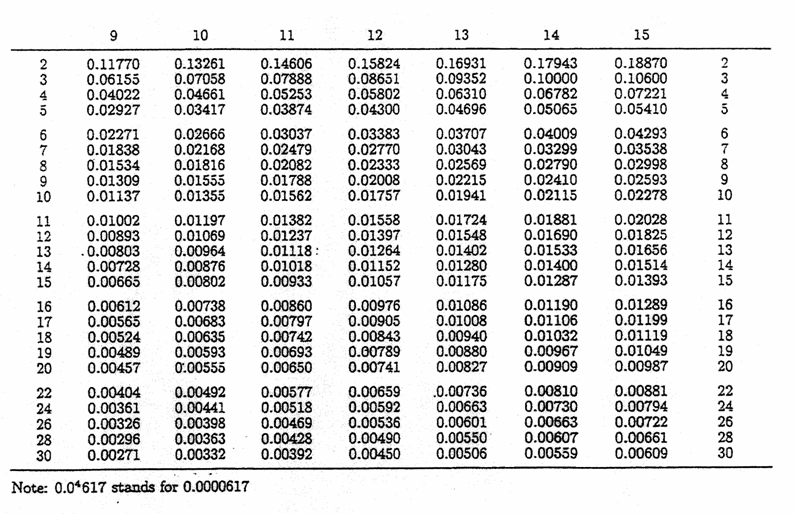
Ovviamente il primo test è da utilizzare quando si ipotizza che una varianza sia nettamente maggiore delle altre, mentre il secondo nella condizione sperimentale opposta.

Valori critici R_(n,p) di Cochran per il confronto simultaneo tra più varianze.

n = numero di osservazioni per gruppo, con campioni bilanciati.

p = numeri di gruppi o varianze a confronto simultaneo.

 

a = 0.05

NUMERO n DI OSSERVAZIONI PER GRUPPO

 

a = 0.01

NUMERO n DI OSSERVAZIONI PER GRUPPO

Valori critici per il test della Varianza minima con  = 0.01

 

 

 

 

Valori critici per il test della Varianza minima con  = 0.05

 

 

 

 

 

C)       Più complessa è la metodologia per il test di significatività approssimato di Bartlett.

Basato su un principio di J. Neyman e E. S. Pearson, figlio di Karl Pearson (vedi, del 1931: On the problem of k samples. Bull. Acad. Polon. Sci. Lett. Ser. A, 3: 460-481), è stato presentato da M. S. Bartlett nel 1937 in due articoli (vedi a: Some examples of statistical methods of research in agriculture and applied biology. Journal Royal Statist. Soc. Suppl. 4: 137-140; vedi b: Properties of sufficiency and statistical tests. Proc. Royal Statist. Soc. Ser. A, 160: 268-282).

 

Nella letteratura statistica è il più diffuso e offre due vantaggi rispetto ai due test precedenti:

- i trattamenti a confronto possono contenere un numero differente di repliche;

- per verificare la significatività tra p gruppi utilizza la distribuzione  con gradi di libertà p-1, più facilmente reperibile delle distribuzioni specifiche precedenti di Hartley e Cochran.

 

Con p misure di varianze campionarie s² che abbiano gradi di libertà n_i, eventualmente tra loro diversi, estratte casualmente da popolazioni distribuite in modo normale, il test approssimato di Bartlett segue una distribuzione c²_(p-1)

fondata sul rapporto

 dove

-  C è il fattore di correzione proposto successivamente per utilizzare la distribuzione  c²_(p-1).

 è uguale a

 e risulta un valore prossimo ad 1.

 

-  M è uguale a

 

 

 con  = media ponderata delle varianze,

 data da

 

Per il calcolo di M (in alcuni testi è indicato con B), in diversi autori propongono l’uso del logaritmo a base 10, preferibile alla logaritmo naturale a base e;

 quindi un altro modo per calcolare M è

 M =

 

Questo test per l’omoschedasticità nel passato era riconosciuta come molto potente, ma solo quando la distribuzione dei dati è normale.

Se la distribuzione dei dati è

-  platicurtica, il valore della probabilità  a calcolata è più alto di quello reale; (il test è conservativo, meno potente: diventa più difficile rifiutare l’ipotesi nulla e quindi è più facile commettere un errore di II Tipo)

-  leptocurtica, il valore della probabilità  a calcolata è più basso di quello reale, rovesciando i concetti  e la conclusione precedenti.

 

Il test può essere applicato su campioni non eccessivamente piccoli, per cui si richiede che ogni varianza sia calcolata su un campione con almeno 5-6 osservazioni.

 

 

D)   Il test di Levene è l’estensione a K gruppi del metodo già illustrato per due campioni indipendenti. E’ l’uso del test ANOVA

-  per valutare se esiste una differenza significativa tra le medie,

-  facendo uso non dei valori osservati, ma dei loro scarti rispetto alla media del gruppo.

Durante gli anni 1950-60, è vivo il dibattito su gli effetti che una distribuzione non normale e varianze non omogenee hanno sui risultati dell’ANOVA per il confronto simultaneo tra più medie. Questo test di Levene è ritenuto da vari statistici più robusto, rispetto alla non normalità della distribuzione, di quanto siano i test di rapporti tra varianze e del test di Bartlett e di tutti i test di confronto tra varianze basate sulla distribuzione F e sulla distribuzione c².

 

Il test di Levene deve la sua diffusione anche all’inserimento in alcuni pacchetti statistici, che lo impongono come verifica preliminare di validità al test t di Student e all’ANOVA.

Per apprendere questi concetti con il linguaggio tecnico adeguato, è utile leggere quanto  Morton B. Brown e Alan B. Forsythe scrivono nel loro articolo del 1974 Robust test for the equality of variances (pubblicato su Journal of the American Statistical Association Vol. 69, pp.: 364-367 a pag. 364): …  the common F-ratio and Bartlett’s test are very sensitive to the assumption that the underlying populations are from a Gaussian distribution. When the underlying distributions are nonnormal, these tests can have an actual size several times larger than their nominal level of significance.

 

Nel 1960 H. Levene con l’articolo Robust Test for Equality of Variances (pubblicato nel volume I. Olkin ed., Contributions to Probability and Statistics, Palo Alto, Calif.: Stanford University Press, pp.:178-292) ha proposto un metodo statistico che richiedeva campioni con un numero di osservazioni uguale.

Nel 1969, da N. R. Draper e W. G. Hunter con l’articolo Transformations: Some Examples Revisited (sulla rivista Technometrics Vol. 11, No. 1, pp.: 23-40) è generalizzato per campioni con  dimensioni differenti.

Del metodo di Levene esistono molte versioni, ma le più diffuse sono tre. La prima è la proposta originaria di Levene.

Le altre due, che ne rappresentano delle modifiche, sono attribuite a Morton B. Brown e Alan B. Forsythe per il loro articolo già citato del 1974 Robust test for the equality of variances (pubblicato su Journal of the American Statistical Association Vol. 69, pp.: 364-367). In esso, al posto della media indicata da Levene, suggeriscono di utilizzare la mediana oppure la media trimmed al dieci per cento (ten percent trimmed mean).

Da qui il nome di Brown-Forsythe test, per queste due varianti o modifiche del test di Levene.

 

La caratteristica distintiva fondamentale di questi test è la misura della tendenza centrale che utilizzano per calcolare gli scarti entro ogni gruppo:

1 -  la media (mean) del gruppo (), per cui entro ciascun gruppo al posto di ogni singolo dato () si usa la differenza () dalla sua media

d_i =

 

2 - la mediana (median) del gruppo (), per cui entro ciascun gruppo al posto di ogni singolo dato () si usa la differenza () dalla sua mediana

d_i =

 

3 - la media trimmed al dieci per cento (ten percent trimmed mean)  del gruppo (), per cui entro ciascun gruppo al posto di ogni singolo dato () si usa la differenza () dalla sua media trimmed

d_i =

 

In modo più specifico,  per la ten percent trimmed mean si intende la media del gruppo, ma dopo che da esso sono stati eliminati il 10% dei valori maggiori e il 10% dei valori minori.

La scelta del 10% oppure di un’altra qualsiasi percentuale è puramente arbitraria.

La scelta di una tra queste tre misure di tendenza centrale dipende dalla forma della distribuzione.

Si impiega

- la media aritmetica, quando la distribuzione dei dati è ritenuta di forma normale, almeno approssimativamente;

- la mediana, quando la distribuzione dei dati è ritenuta asimmetrica;

- la media trimmed quando nella distribuzione dei dati sono presenti valori ritenuti anomali.

Brown e Forsythe indicano come appropriata la media trimmed, quando i dati hanno una distribuzione vicina a quella di Cauchy, caratterizzata appunto da una fortissima asimmetria.

Inoltre sono state proposte numerose varianti di ognuna di queste.

 

Ad esempio, dopo aver calcolato lo scarto dalla media o dalla mediana, tra le varianti più diffuse possono essere ricordate le trasformazioni

     e     

 per rendere le distribuzioni degli scarti ancor più simili a quella normale. Ma, con la motivazione che per quanto riguarda la normalità, il test t di Student e il test ANOVA sono robusti, le trasformazioni effettuate su gli scarti abitualmente sono tralasciate.

 

Il Trimming data o semplicemente Trimming è

-  l’eliminazione di una percentuale prefissata di valori estremi.

Può essere fatta in entrambe le code o in una coda sola della distribuzione dei dati, sulla base delle caratteristiche del fenomeno. Anche la quota di estremi da eliminare è molto variabile, potendo essere

-  solo il valore più alto e quello più basso,

-  il primo e l’ultimo cinque per cento,

-  il primo e l’ultimo quartile (25%),

-  altre quote tra il minimo di un dato e il massimo di un quarto dei dati.

E’ relativamente frequente la scelta di prendere in considerazione solamente il 50% dei valori centrali, come appunto si ottiene eliminando il primo e l’ultimo quarto. La media di questa distribuzione è chiamata media interquartile e viene utilizzata quando la proporzione di outlier in entrambe le code è molto alta.

 

La Winsorization (la tecnica è chiamata winsorizing) non elimina i valori più estremi, ma li sostituisce con altri meno estremi.

E’ una tecnica semplice, che serve per attenuare l’effetto di possibili outlier, quando i dati raccolti servono per il calcolo delle statistiche del campione o per test successivi.

 

Ad esempio, si supponga di avere ottenuto la seguente serie di 13 valori, qui ordinata

 

 

 

  e la cui media è  = 49,5.

E semplice rilevare dalla lettura dei dati, quindi a posteriori, che sono presenti due valori molto differenti da tutti gli altri, in entrambi gli estremi (i valori 0 e 1 nella coda sinistra; 154 e 322 nella coda destra).

Può essere utile costruire una nuova distribuzione, sempre di  dati; quindi senza diminuire le dimensioni del campione. Questi estremi in entrambe le direzioni sono sostituiti dal terzo valore, quello a loro più vicino, ottenendo la seguente serie di dati

 

 

 

 

 la cui media è  = 18,7.

La mediana delle due distribuzioni dei 13 valori è 18. Si osservi come la seconda media (18,7) sia molto vicina alla mediana (18), che ovviamente è rimasta immutata, mantenendo  costante.

Questo metodo è da utilizzare soprattutto quando sono presenti valori indefiniti (come < 1  oppure > 100). Sono misure che si riscontrano quando la variabilità delle quantità presenti nei campioni è nettamente inferiore oppure superiore al campo di misura dello strumento, che è preciso solo per valori intermedi.

Il trimming può essere simmetrico, come in questo caso; ma può anche essere asimmetrico, quando l’operazione coinvolge un numero di dati differenti nelle due code della distribuzione.

 

Una volta definito quale misura di tendenza centrale utilizzare, si ricava che gli scarti rispetto al valore centrale sono sia positivi sia negativi. Per averle tutti positivi, eliminando i segni negativi,

- sono prese in valore assoluto

d_i =

 

Per confrontare la varianza di K gruppi (A , B, C),

 con ipotesi nulla

H₀: s²_A = s²_B = s²_C

 contro l’ipotesi alternativa

H₁: non tutte le s² sono uguali     oppure    H₁: almeno due s² sono diverse tra loro

 

 la proposta di Levene consiste

-  nell’applicare alla k serie di scarti (al quadrato o in valore assoluto) l’analisi della varianza a un criterio,

-  nell’assunzione che, se i valori medi degli scarti risultano significativamente diversi, le k varianze dei dati originali sono diverse.

 

Con un linguaggio più tecnico, se utilizzando gli scarti dalla media si rifiuta l’ipotesi nulla

H₀: m_A = m_B = m_C

 per accettare l’ipotesi alternativa

H₁: non tutte le m sono uguali   oppure  H₁: almeno due m sono diverse tra loro

implicitamente deriva che

 sui dati originali si rifiuta l’ipotesi nulla

H₀: s²_A = s²_B = s²_C

 per accettare l’ipotesi alternativa

H₁: non tutte le s² sono uguali       oppure      H₁: almeno due s² sono diverse tra loro

Come nell’analisi della varianza ad un criterio, i gruppi possono avere un numero differente di osservazioni.

In termini più formali, indicando

-  con  lo scarto in valore assoluto di ogni valore  dalla media  del suo gruppo

 

-  con  lo scarto in valore assoluto di ogni valore  dalla media  del suo gruppo

- con  la media di un gruppo di ,

- con  la media generale degli  ,

 si calcola il valore

 

Si rifiuta l’ipotesi nulla, quindi le varianze sono statisticamente differenti, quando

 vale a dire quando  è maggiore del valore critico della distribuzione  alla probabilità  prefissata e i gradi di libertà corrispondenti alla devianza tra e alla devianza d’errore.

 

Diversi autori sono molto critici sull’uso dei test per l’omogeneità della varianza. Infatti essi sono

- fortemente alterati dalla non normalità della distribuzione

-  e con pochi dati è impossibile verificare se le varie distribuzioni campionarie possano essere ritenute prossime alla normale.

Inoltre, le varianze campionarie s² devono evidenziare differenze molto grandi per risultare significative, poiché i test sono impostati per non rifiutare l’ipotesi nulla in condizioni d’incertezza. Può quindi essere frequente il caso in cui varianze s², anche se rilevanti sotto l’aspetto ecologico od ambientale, non risultano significative ai test per l’omogeneità.

 

ESEMPIO 1  (TEST DI HARTLEY, COCHRAN E BARTLETT CON GLI STESSI DAT).   Per verificare l'esistenza di differenze nella qualità dell'aria, in 4 zone di una città si è misurata la quantità di solventi aromatici in sospensione.

 

 

Con le osservazioni riportate nella tabella, si intende verificare se le varianze dei quattro gruppi possono essere ritenute omogenee.

 

Risposta.  Si calcolano dapprima le 4 varianze,

 

 

 

 ricordando che ognuna di esse ha 4 gdl.

L’ipotesi nulla è

H₀ :  s²_I = s²_II = s²_III = s²_IV

 mentre l’ipotesi alternativa H₁ è che almeno una di esse sia diversa.

 

A) Con il metodo di Hartley, si calcola il rapporto tra la varianza maggiore (335,7) e la varianza minore (63,2): si ottiene un F con indici 4 (numero di gruppi) e 4 (numero di osservazioni entro ogni gruppo meno 1)

 che risulta uguale a 5,30.

Per la significatività si confronta il valore calcolato (5,3) con il valore tabulato alla probabilità prefissata per il medesimo numero di gruppi (4) e di gdl entro gruppi (4): per a = 0.05 risulta 20,6.

 

B) Con il metodo di Cochran si stima  un rapporto R

 

 

 che per n uguale a 5 e p uguale a 4 risulta 0,57

Nelle tabelle, il valore critico

-  alla probabilità a = 0.01 risulta uguale a 0,7212

-  alla probabilità a = 0.05 risulta uguale a 0,6287.

Il valore calcolato (0,57) è inferiore a questo ultimo (0,6287), per cui non è dimostrata una differenza significativa tra le 4 varianze.

 

C) Con il metodo di Bartlett, si deve dapprima calcolare la varianza media

 

 

dividendo la somma delle 4 devianze per la somma dei gradi di libertà:

 

 =  = 147,1

 

Successivamente si stimano

- sia il valore di M

 che, con i dati dell’esempio,

M = =

= 16 x 4,991 - (4 x 4,146 + 4 x 4,573 + 4 x 4,529 + 4 x 5,816) =

= 79,856 - (16,584 + 18,292 + 18,116 + 23,264)  =  79,856 - 76,256 = 3,60

 

 risulta M = 3,60;

 

- sia il valore di C

 che risulta

C  =  1+   =   1+  =

= 1 + 0,111×(1 - 0,0625) = 1 + (0,111 x 0,9375) = 1 + 0,104 = 1,104

 

 uguale a 1,104 (non lontano da 1, come quasi sempre).

Il valore del  (chi quadrato con 3 gradi di libertà)

 =   =   = 3,26

è uguale a 3,26.

Nella tabella dei valori critici alla probabilità a = 0.05 il valore tabulato è 7,81.

Il valore calcolato (3,26) è inferiore: non si può rifiutare l’ipotesi nulla.

Secondo il risultato del test, i 4 gruppi a confronto hanno varianze non significativamente diverse.

 

Ma quale valore a un test sull'omogeneità della varianza?

Per accettare le conclusioni raggiunte mediante l’analisi, restano le perplessità già evidenziate sulla potenza di questi test e quelle che derivano dal numero ridotto di osservazioni per campione, come nel caso dell’esempio utilizzato.

 

D) Il test di Levene applica l’analisi della varianza ad un criterio e i gruppi possono avere un numero differente di osservazioni. A differenza dei tre test precedenti, può essere applicato solo disponendo dei dati originali, non delle loro varianze

 

 

ESEMPIO 2. (TEST DI LEVENE).  Riprendendo gli stessi dati dei tre test precedenti sulla omoscedaticità di k gruppi (dopo aver tolto due valori per costruire campioni non bilanciati)

 

 

 

verificare se le varianze dei 4 gruppi sono tra loro statisticamente differenti.

 

Risposta.

1 -  Si calcolano le medie dei 4 gruppi

 

 

2 - Utilizzando gli scarti in valore assoluto, dalla tabella

 

 

 

 e dai calcoli preliminari

= 2.696,5                 = 166,3

= 27,6         = 23,0             = 37,2          = 78,5

 

 si stimano le devianze

 

 

 

 

 e si completa la tabella dell’ANOVA

 

 

 

3 -  Essa conduce alla stima

 

  di F = 4,453 con gdl 3 e 14.

Il valore critico con gdl 3 e 14

-  alla probabilità a = 0.05 è uguale a 3,34

-  alla probabilità a = 0.025 è uguale a 4,24

-  alla probabilità a = 0.01 è uguale a 5,35

Le 4 varianze a confronto risultano significativamente differenti, con una probabilità inferiore al 2,5%

 

Se al posto della media viene utilizzata la mediana, la metodologia è del tutto analoga.

Vari autori e alcuni programmi informatici preferiscono l’uso della mediana. E’ chiamato in modi diversi e i più diffusi sono due:

-  Levene median test,

-  Modified-Levene Equal-Variance Test.

 

I quattro test proposti sono validi quando la distribuzione dei dati è normale; con l’allontanamento da essa, a causa di asimmetria e/o curtosi, tutti subiscono variazioni nella potenza e nella loro attendibilità, ma in modo diverso. Per ovviare a questi inconvenienti, spesso è raccomandato il ricorso ai test non parametrici, presentati nei capitoli relativi (vedi indice).

 

Su tutti questi risultati permane il dubbio filosofico che l’uguaglianza delle varianze non è mai dimostrato, quando l’ipotesi nulla non è rifiutata.