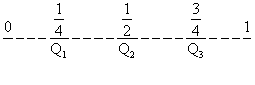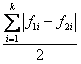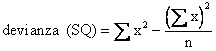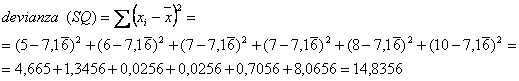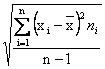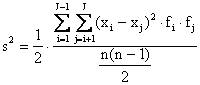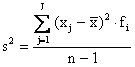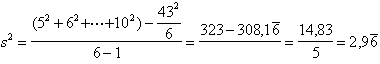elementi di statistica descrittiva

Per DISTRIBUZIONI UNIVARIATe

1.7. MISURE DI DISPERSIONE O VARIABILITA'

La dispersione o variabilità è la seconda importante caratteristica di una distribuzione di dati. Essa definisce la forma più o meno raccolta della distribuzione intorno al valore centrale e fornisce indicazioni sul tipo di test da applicare; nei capitoli successivi verrà dimostrato come per confrontare le medie di due o più campioni sia richiesta l’omogeneità della varianza.

1.7.1 La prima misura ad essere stata storicamente utilizzata per descrivere la dispersione o variabilità dei dati è il campo o intervallo di variazione, definito come la differenza tra il valore massimo e quello minimo.

Intervallo di variazione = Valore massimo - valore minimo

Ha il grande vantaggio di essere un metodo intuitivo e molto semplice, in particolare quando i dati sono ordinati.

Tra gli inconvenienti di questa misura sono da prendere in considerazione:

- l'incapacità di sapere come i dati sono distribuiti entro l'intervallo, in particolare di dedurre la presenza di valori anomali;

- la sua dipendenza dal numero di osservazioni. All’aumentare del numero dei dati, cresce anche la probabilità di trovare un valore minore del minimo precedente ed uno maggiore di quello massimo precedente.

L’intervallo di variazione è quindi una misura poco efficiente della dispersione dei dati: per un confronto omogeneo tra distribuzioni, sarebbe necessario avere campioni delle stesse dimensioni, una condizione operativa eccessivamente limitante per la ricerca e l’analisi dei dati.

1.7.2 La differenza interquartile (figura 18), la differenza tra il 3° (Q₃) ed il 1° (Q₁) quartile ha il vantaggio di eliminare i valori estremi, ovviamente collocati nelle code della distribuzione. Tuttavia le proprietà di questa semi-differenza, chiamata anche scarto interquartile, non sono sostanzialmente differenti da quelle del campo di variazione.

Figura 18. Differenza interquartile = 3°quartile (Q₃) - 1°quartile (Q₁)

Come misure di posizione non-centrale, ma con finalità esclusivamente descrittive, sono spesso usati i quantili, chiamati anche frattili, in quanto ogni sottogruppo contiene la stessa frazione di osservazioni. Quelli più comunemente usati sono i decili, che classificano i dati ordinati in decine, ed i percentili, che li suddividono in centesimi. Con i quantili, si possono individuare quali sono i valori che delimitano, nel margine inferiore o superiore della distribuzione, una percentuale o frazione stabilita di valori estremi. Per esempio, nello studio dell'inquinamento, come di qualunque altro fenomeno, può essere utile vedere quali sono le zone o i periodi che rientrano nell’1, nel 5 o nel 10 per cento dei valori massimi o minimi. A valori così rari, facilmente corrispondono cause anomale, che di norma è interessante analizzare in modo più dettagliato. Nello studio di qualunque fenomeno biologico od ecologico, le misure particolarmente piccole o eccezionalmente grandi rispetto ai valori normali quasi sempre evidenziano cause specifiche, meritevoli di attenzione.

Quando la forma della distribuzione è ignota o risulta fortemente asimmetrica, l'uso dei quantili fornisce indicazioni operative semplici e robuste per individuare i valori più frequenti, da ritenersi “normali” e quelli meno frequenti od “anomali”.

Gli scarti dalla media sono la misura più appropriata della variabilità di un insieme di dati. Ma poiché la loro somma è sempre nulla per definizione, in quanto la media è il baricentro della distribuzione, è necessaria una trasformazione che potrebbe essere attuata in due modi:

a) gli scarti assoluti dalla media;

b) i quadrati degli scarti dalla media.

1.7.3 Lo scarto medio assoluto dalla media per dati semplici

è dato da

e per raggruppamenti in classi è ottenuto con

dove

- x_i = valore dell’i-esimo dato in una distribuzione semplice,

- = valore centrale della classe in una distribuzione di frequenza,

- n = numero totale di dati,

- n_i = numero di dati della classe i in una distribuzione di frequenza.

Un indice analogo, usato nelle discipline sociali ed economiche per valutare la diversità tra due distribuzioni di frequenze relative, è

l’indice semplice di dissomiglianza (D)

D =

dove 1 e 2 sono i due gruppi e k sono le classi.

D è uguale a 0 quando le due distribuzioni di frequenza relativa sono identiche e uguale a 1 quando la prima distribuzione è tutta concentrata in una classe e l’altra distribuzione in una classe diversa.

1.7.4 In alcuni test di statistica non parametrica, come misura di dispersione è utilizzato lo scarto medio assoluto dalla mediana, che è la media degli scarti assoluti dei singoli dati dalla loro mediana; le formule sono uguali alle due precedenti, sostituendo la mediana alla media.

E’ proprietà specifica della mediana rendere minima la somma degli scarti assoluti. Di conseguenza, lo scarto medio assoluto dalla mediana è sempre inferiore allo scarto medio assoluto dalla media; i due valori sono uguali solamente quando la distribuzione è simmetrica e quindi media e mediana coincidono.

1.7.5 La Devianza o Somma dei Quadrati (SQ) degli scarti dalla media (SS = Sum of Squares, in inglese) è la base delle misure di dispersione dei dati, utilizzate in tutta la statistica parametrica. Tutta la statistica parametrica è fondata sulla devianza e sulle misure da essa derivate.

(1 )

L'equazione precedente è la formula di definizione od euristica. Spesso è poco pratica, in particolare quando la media è un valore frazionale, con vari decimali. Diviene allora conveniente ricorrere a un'altra formula, algebricamente equivalente, che permette di effettuare i calcoli manuali in tempi più brevi e con una sola approssimazione finale, chiamata formula empirica od abbreviata:

(2)

dove:

- = sommatoria dei valori dopo che ogni osservazione è stata elevata al quadrato,

- = sommatoria di tutti i dati, elevata al quadrato,

- n = numero di osservazioni sulle quali è stata calcolata la somma.

ESEMPIO. Calcolare con la formula euristica (1) e con quella abbreviata (2) la devianza (SQ) dei 6 numeri seguenti: 5, 6, 7, 7, 8, 10.

Risposta.

1. Con la formula euristica, si deve calcolare dapprima la media:

ed in seguito la devianza (SQ),

intesa come Somma dei Quadrati degli scarti di ogni valore dalla media:

2. Con la formula abbreviata, calcolare direttamente il valore della devianza (SQ), dopo aver fatto sia la somma dei dati precedentemente elevati al quadrato, sia il quadrato della somma dei dati, secondo l’annotazione algebrica seguente

I due valori della devianza spesso non risultano identici, in particolare quando stimati con più cifre decimali, a causa dell’approssimazione con la quale è calcolata la media, se non risulta un valore esatto. In questi casi, è da ritenersi corretta la stima fornita dalla formula abbreviata, che non richiede approssimazioni nei calcoli intermedi.

E’ utile ricordare che, per distribuzioni di dati raggruppati in classi, la formula euristica diventa

dove

- è il valore centrale di ogni classe e

- è la media generale della distribuzione.

Il valore della devianza dipende da 2 caratteristiche della distribuzione: gli scarti di ogni valore dalla media ed il numero di dati. La prima è una misura della dispersione o variabilità dei dati ed è l’effetto che si intende stimare; la seconda è un fattore limitante per l’uso della devianza, in quanto un confronto tra 2 o più devianze richiederebbe campioni con lo stesso numero di dati. Pertanto, per una misura di dispersione dei dati che sia indipendente dal numero di osservazioni, si ricorre alla varianza.

1.7.6 La varianza o Quadrato Medio (QM, in italiano; MS da Mean Square, in inglese) è una devianza media o devianza rapportata al numero di osservazioni.

La varianza di una popolazione (1), il cui simbolo è , è ottenuta dividendo la devianza per n, il numero di osservazioni.

(1)

La varianza di un campione (2), il cui simbolo è , è ottenuta dividendo la devianza per n-1, il numero di gradi di libertà.

(2)

Ovviamente, quando n è grande le differenze tra varianza della popolazione e varianza del campione sono minime; quando n è piccolo, le differenze sono sensibili.

E' importante ricordare che quando si parla di inferenza, cioè quando si utilizzano i dati di un campione per conoscere le caratteristiche della popolazione, si usa sempre la varianza campionaria.

Le giustificazioni logiche dell'uso di dividere la devianza per n-1, detta anche correzione di Student, sono lunghe e complesse: la più semplice si basa sul fatto che n-1 è il numero di osservazioni indipendenti, chiamato gradi di libertà, abbreviato abitualmente in gdl o df (da degree freedom). Poiché la somma degli scarti dalla media è uguale a 0, l'ultimo valore di una serie è conosciuto a priori, non è libero di assumere qualsiasi valore, quando siano già noti i precedenti n-1 valori.

Come concetto generale introduttivo, si può dire che il numero di gradi di libertà è uguale al numero di dati meno il numero di costanti che sono già state calcolate o di informazioni che siano già state estratte dai dati. Nel caso specifico della varianza, la costante utilizzata per calcolare gli scarti è la media: quindi i gradi di libertà sono n-1.

Mentre la media è un valore lineare, la varianza è un valore al quadrato; per stime associate alla media o per confronti con essa, è necessario ricondurla a un valore lineare.

1.7.7 Lo scarto quadratico medio o deviazione standard, il cui simbolo è  nel caso della popolazione ed s nel caso di un campione, è la radice quadrata della varianza. Il termine standard deviation e il suo simbolo s (la lettera greca sigma minuscola) sono attribuiti al grande statistico inglese Karl Pearson (1867 – 1936) che l’avrebbe coniato nel 1893; in precedenza era chiamato mean error. In alcuni testi di statistica è abbreviato anche con SD ed è chiamato root mean square deviation oppure root mean square,

E’ una misura di distanza dalla media e quindi ha sempre un valore positivo. E' una misura della dispersione della variabile casuale intorno alla media.

Nel caso di un campione, a partire da una serie di dati la deviazione standard, il cui simbolo è s, può essere calcolata come:

deviazione standard (s) =

dove

- x_i = valore del dato in una distribuzione semplice,

- = valore centrale della classe in una distribuzione di frequenza,

- n_i = numero di dati della classe i in una distribuzione di frequenza,

- n = numero totale di dati.

1.7.8 L’errore standard (standard error, in inglese) è indicato con es e misura la dispersione delle medie calcolate su n dati, come la deviazione standard serve per la dispersione dei dati.

L’errore standard es è

es =

ESERCIZIO. Calcolare media, devianza, varianza e deviazione st. e errore st. di : 9 6 7 9 8 8.

Risposta:

media = 7,833; devianza = 6,8333; varianza = 1,367; deviazione st. = 1,169; errore standard = 0,477

Per l’uso della varianza, che sarà fatto nei capitoli dedicati all’inferenza, è importante comprendere che la varianza tra una serie di dati rappresenta una misura di mutua variabilità tra di essi.

Essa può essere calcolata in tre modi:

1 - come la metà della media aritmetica del quadrato di tutti gli n(n-1)/2 scarti possibili tra coppie di osservazioni,

2 - mediante gli scarti tra i dati e la loro media,

3 - mediante la formula abbreviata.

1 - Il primo metodo utilizza gli scarti tra tutte le possibile coppie di dati; è una procedura molto lunga, che serve per comprendere il reale significato della varianza tra dati o tra medie:

2 - Il secondo metodo rappresenta la formula euristica, quella che definisce la varianza, come confronto con il valore medio:

3 - Il terzo metodo è una delle varie versioni della formula abbreviata, quella che serve per semplificare i calcoli manuali e ridurre i tempi per il calcolo

ESEMPIO. Calcolare la varianza di 6 dati (5, 6, 7, 7, 8, 10) mediante le 3 formule proposte, per dimostrare empiricamente la loro equivalenza (ricordando che, in questo esempio, f_i = 1).

Risposta:

1. Utilizzando gli scarti assoluti (j - i) tra tutte le possibili coppie di dati, riportati nella matrice triangolare sottostante:

j\i	5	6	7	7	8	10
5	0
6	1	0
7	2	1	0
7	2	1	0	0
8	3	2	1	1	0
10	5	4	3	3	2	0

si ottiene

2. Mediante gli scarti dalla media ()

si ottiene

3. Ricorrendo alla formula ridotta

si ottiene

1.7.9 Il coefficiente di variazione (coefficient of variation oppure coefficient of variability) è una misura relativa di dispersione, mentre le precedenti erano tutte misure assolute. E' quindi particolarmente utile ricorrere ad esso, quando si intende confrontare la variabilità di due o più gruppi con medie molto diverse oppure con dati espressi in scale diverse.

Consideriamo come esempio il confronto tra la variabilità di due specie animali con dimensioni medie sensibilmente diverse, come tra i cani e i cavalli. La varianza tra cavalli di razze diverse è superiore a quella esistente tra i cani, perché gli scarti assoluti dalla media della specie sono maggiori. Ma spesso il problema consiste nel fare un confronto relativo tra variabilità e dimensioni medie delle due specie; allora il rapporto tra il cane di dimensioni maggiori e quello di dimensioni minori risulta superiore a quello esistente nei cavalli.

Il Coefficiente di Variazione (CV oppure semplicemente con V in molti testi recenti) misura la dispersione percentuale in rapporto alla media.

Per una popolazione:

dove

= deviazione standard della popolazione

media della popolazione

Per un campione:

dove

- s = deviazione standard del campione

- = media del campione

Quando è calcolato su dati campionari, in particolare se il numero di osservazioni è limitato, il coefficiente di variazione CV deve essere corretto di una quantità 1/4N, dove N è il numero di osservazioni del campione. Di conseguenza,

il coefficiente di variazione corretto V’ diventa

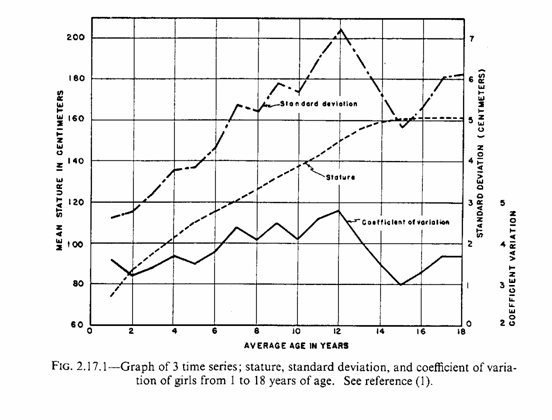
La figura successiva (tratta da pag. 16 di George W. Snedecor, William G. Cochran del 1974, Statistical Methods, Iowa University Press Ames, Iowa, U.S.A. sixth edition , seventh printing, pp. XIV + 593) è utile per spiegare i concetti già presentati:

- con la linea tratteggiata descrive l’altezza media di gruppi di ragazze da 1 a 18 anni d’età, che varia da circa 70 cm. ad oltre 170 cm.; la scala di riferimento è riportata sulla sinistra e varia da 60 a 200 centimetri;

- con la linea formata da tratti e punti alternati descrive la deviazione standard dell’altezza di ogni gruppo d’età; la scala è riportata sulla destra (parte superiore) e i valori variano da 0 a 7;

- con la linea continua descrive il coefficiente di variazione; la scala è riportata a destra nella parte inferiore più esterna ed i valori variano da 2 a 5.

E’ importante osservare come la media e la sua deviazione standard aumentino in modo quasi correlato, mentre il CV resta costante intorno al 4%:

In natura, il coefficiente di variazione tende ad essere costante per ogni fenomeno, con valori che abitualmente oscillano tra il 5% e il 15%. Valori esterni a questo intervallo possono fare sorgere il sospetto di essere in presenza di un errore di rilevazione o di calcolo; si tratta comunque di situazioni non usuali che occorrerebbe spiegare, individuandone la causa. Nell’esempio precedente, si tratta di individui della stessa età.

Se il materiale biologico in esame ha un CV troppo basso (2-3 %), si può sospettare l'esistenza di un fattore limitante che abbassa notevolmente od elimina la variabilità, come la presenza di omogeneità genetica congiunta ad una situazione ambientale uniforme; viceversa, un CV molto alto (50%) è indice della presenza di condizioni anomale o molto differenti contemporaneamente per più fattori.

Per l'uomo, il coefficiente di variazione dell’altezza è stato calcolato tra il 40% e il 45%, testimoniando l'esistenza nella specie di grandi differenze, dovute sia a cause genetiche che ambientali (alimentazione, condizioni sanitarie, ecc.).

Quando per misurare lo stesso fenomeno si utilizzano scale differenti, ad esempio l’altezza misurata in centimetri o in pollici, la media e la deviazione standard cambiano, ma il CV resta uguale.

Esso può essere calcolato anche per campioni; ma quando il numero di dati è limitato, la sua stima può indurre in errore.

In laboratorio per valutare la qualità dei reagenti, spesso si ricorre al C.V.: i reagenti che determinano il CV minore sono quelli di qualità superiore, poiché forniscono risposte meno variabili in rapporto ai valori medi.

1.7.10 La varianza in dati raggruppati: correzione di Sheppard

La varianza calcolata in una distribuzione di frequenza di misure continue è approssimata; la sua stima è fondata sull’ipotesi di distribuzione uniforme entro ogni classe e quindi si presume che il valore centrale di ogni classe corrisponda alla sua media. In realtà, la varianza calcolata sui dati reali e quella stimata a partire dal raggruppamento in classi non sono uguali.

Quando la distribuzione dei dati è normale, entro ogni classe i valori più vicini alla media generale sono sempre più numerosi di quelli più distanti, collocati verso gli estremi.

Come già evidenziato, per il calcolo della media, le approssimazioni nella parte sinistra del valore centrale compensano le approssimazioni fatte nella parte destra: la media calcolata direttamente dai dati e quella calcolata con il raggruppamento in classi hanno solo differenze casuali, di solito di entità ridotta.

Il coefficiente di variazione è un numero puro, svincolato da ogni scala di misura e dalla tendenza centrale del fenomeno studiato. Secondo molti, appunto perché un rapporto, avrebbe significato solamente se calcolato per variabili misurate con una scala di rapporti.

Per il calcolo della varianza, le approssimazioni di segno opposto nelle due parti della media sono elevate al quadrato: di conseguenza, non si compensano, ma si sommano. In una popolazione con un numero molto alto di dati, la varianza calcolata dal raggruppamento in classi è sistematicamente maggiore di quella reale, quella calcolata direttamente dai dati originari. Le differenze crescono all'aumentare della misura dell'intervallo di ogni classe, poiché aumenta l’imprecisione.

Pertanto si deve apportare una correzione, detta

correzione di Sheppard, proposta appunto da W. F. Sheppard nel 1898 sulla rivista Proceeding London Mathematical Society e riportata in vari testi, tra cui Statistical Methods di George W. Snedecor e William G. Cochran (1967, Iowa State University Press).

Consiste nel sottrarre alla varianza calcolata un valore pari a

per cui

dove

- h è l'ampiezza delle classi e

- 12 è una costante.

ESEMPIO. In una distribuzione di frequenza, in cui le classi hanno ampiezza costante con intervallo h = 10, è stata calcolata una varianza s² = 50; la varianza corretta, quella che si sarebbe ottenuta utilizzando i singoli valori, secondo Sheppard dovrebbe essere

uguale a 41,66 come risulta dal calcolo mostrato.

Questa relazione è ritenuta valida per le popolazioni.

Con campioni formati da pochi dati, non è facile, spesso non è possibile, verificare se la distribuzione sperimentale utilizzata rispetti le tre condizioni fissate da Sheppard per applicare la correzione:

- essere continua;

- avere un intervallo di ampiezza finito;

- tendere a zero in modo graduale nelle due code della distribuzione.

Quando si dispone solo di piccoli campioni, la correzione potrebbe essere non adeguata alla forma della distribuzione e determinare un errore maggiore.

Di conseguenza, per piccoli campioni come quelli usati nella ricerca ambientale, la quasi totalità dei ricercatori preferisce non applicare questa correzione, ma usare direttamente la varianza calcolata dalla distribuzione di frequenza, in qualunque modo sia stato fatto il raggruppamento in classi.