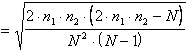7.3.   IL Test delle successioni per un campione

 

 

Quando si dispone di un solo campione, i quesiti di inferenza statistica che ricorrono con maggior frequenza riguardano la verifica di un accordo della distribuzione osservata con una distribuzione teorica od attesa. E’ quanto già discusso nel capitolo III, in cui la distribuzione attesa può essere stimata sulla base di qualsiasi legge matematica, statistica o biologica.

Un secondo gruppo importante di inferenze applicate ad un campione riguarda la verifica della tendenza centrale in una distribuzione simmetrica, sia intorno allo zero che a qualsiasi altro valore. Come già presentato nei capitoli precedenti di statistica parametrica, sono utilizzati il test Z o il test t, in rapporto al fatto che si conosca la varianza della popolazione o che si debba ricorrere a quella campionaria come sua stima migliore.

Quando la distribuzione non è normale o il tipo di scala è ordinale, si può ricorrere ai test presentati nei capitoli successivi. Prima di essi è tuttavia importante discutere il test delle successioni, in quanto non ha l’equivalente in statistica parametrica ed è utile in varie circostanze.

 

Il test delle successioni per un campione o per risposte alternative (Run test with two attributes), già illustrato da J. V. Bradley nel suo testo di Statistica non parametrica del 1968 (intitolato Distribution-free Statistical Test, edito da Englewood Cliffs, NJ: Prentice Hall), è utilizzato nel caso di osservazioni raccolte in una successione temporale o in una successione geografica, a partire da un punto origine. Permette di saggiare se, in riferimento all'ordine, alla sequenza, alla successione (run) o serie (termini sinonimi), i dati del campione sono casuali.

E' un quesito che nella ricerca sperimentale si pone spesso, sia in laboratorio che in natura: verificare se i risultati positivi e negativi, i valori alti e bassi di una serie temporale di osservazioni oppure due categorie di eventi alternativi si succedono nel tempo o nello spazio con casualità. Infatti essi potrebbero non essere casuali, ma aggregarsi o alternarsi con regolarità prevedibile, come può avvenire nei fenomeni ciclici.

L'importanza del test per l’analisi delle successioni deriva anche dall’essere privo di alternative: non esistono test analoghi nella statistica parametrica.

Il test può essere applicato per dati binari, tipici di un processo binomiale. Può anche essere esteso a dati continui, misurati con scale d'intervalli o di rapporti, ma solo dopo trasformazione in risposte binarie. Ad esempio, con misure continue si ottiene una distribuzione binomiale (valori alti e valori bassi), mediante il confronto di ogni singola misura con un valore stimato o prefissato, come la mediana o un qualsiasi valore soglia.

 

Per chiarire più compiutamente i concetti relativi alla successione di eventi casuali e ai casi in cui questo test può essere applicato, è utile un esempio.

 

Si supponga di lanciare una moneta 15 volte e che si ottenga 8 volte testa (T) e 7 volte croce (C), con la seguente serie temporale

 

T  C  T  C  T  C  T  C  T  C  T  C  T  C  T

 

E' evidente la sua non casualità, che si riferisce non al numero di T e di C, la cui probabilità può essere calcolata con il test binomiale, ma al regolare alternarsi degli eventi. Parimenti non casuale sarebbe stata una serie, identica come numero di dati alternativi T (8) e C (7), ma in sequenza differente,

T   T   T   T   T   T   T   T   C   C   C   C   C   C   C

 che concentra nella prima parte tutti gli eventi di un tipo e nella seconda quelli dell'altro tipo.

 

La verifica degli effetti sistematici o periodici è fondata sul conteggio delle successioni, definite come il numero di simboli identici preceduti o seguiti da simboli differenti o da nessun simbolo.

Nel primo caso dell’esempio, il numero delle successioni è

 

 

 15, come il numero di osservazioni che ne rappresenta il valore massimo;

 nel secondo caso è

 

 solamente 2, come il numero di eventi alternativi e che rappresenta il numero minimo.

E' intuitivo che la successione dei 15 lanci della moneta non può essere ritenuta casuale, in nessuno dei due casi teorici presentati. E’ evidente una legge dell’alternanza nel primo caso e di concentrazione nel secondo, che permettono di indovinare con facilità il risultato di eventuali lanci successivi.

Essi rappresentano i due casi estremi di tutti i modi, in cui è possibile disporre gli elementi dei due gruppi.

In un gruppo di N oggetti di cui n₁ di tipo 1 e n₂ di tipo 2 si hanno

 

 possibili differenti ordini differenti.

Nell’esempio precedente con N = 15, n₁ = 8  e  n₂ = 7  sono

 

 6435 ordini differenti.

Ognuno di essi è caratterizzato da un numero specifico di successioni, che in totale hanno una distribuzione approssimativamente o asintoticamente normale, per campioni sufficientemente grandi.

 

Un campione può ragionevolmente essere ritenuto casuale solamente quando il numero delle successioni non è né troppo grande né troppo piccolo. Per essere casuale, il numero di successioni deve tendere ad una frequenza media (), che dipende dal numero dei due eventi alternativi; essa può essere calcolata con la formula

 

 dove

-           è la media aritmetica attesa delle successioni,

-          n₁  è il numero di eventi di un tipo,

-          n₂  è il numero di eventi dell'altro tipo,

-          N  è il numero totale di dati od osservazioni.

Applicata sempre allo stesso esempio teorico, con   N = 15,  n₁ = 8 e n₂ = 7, la media stimata o attesa (m_r) del numero di successioni (runs), nell’ipotesi che H₀  (distribuzione casuale di T e C) sia vera

 

m_r  =    =  8,4

 è uguale a 8,4.

In questo modo, il quesito sulla casualità delle successioni è trasformato nel problema di verificare se il numero di successioni contato nella serie sperimentale di dati (15 o 2) sia significativamente differente dal valore medio atteso (8,4).

Nella condizione che l'ipotesi nulla H₀ sia vera (totale casualità degli eventi nella loro successione temporale), la differenza tra il numero di successioni osservate e il numero atteso segue una distribuzione approssimativamente normale, quando le dimensioni dei due campioni sono grandi. La probabilità relativa può essere calcolata mediante

 

 dove

-          R  è il numero di successioni (Runs) osservate,

-           è la media attesa di successioni, nella condizione che l'ipotesi nulla H₀ sia vera,

-           è la deviazione standard della media e può essere calcolata da

 

s_r

 sulla base

-          del numero di dati n₁ e n₂ dei due eventi alternativi e

-          del numero totale N di osservazioni.

 

Nell’uso di questo test, l’ipotesi che ricorre con frequenza maggiore riguarda un numero troppo ridotto di successioni. Nella ricerca etologica può essere, in animali a struttura sociale di tipo gerarchico, la modalità d’accesso al cibo d’individui appartenenti a due livelli sociali diversi o la precedenza degli anziani rispetto ai giovani. Nella ricerca ambientale, è il caso della successione di depositi geologici in una sezione, della quale si intenda verificare la non casualità dei differenti strati risalenti a due tipologie diverse.

 

Per piccoli campioni (n₁ e n₂ < 20), la distribuzione delle probabilità è distorta rispetto a quella normale. In tali condizioni, la significatività deve essere fornita da tabelle che riportano le frequenze critiche minime e massime. Nelle due pagine precedenti sono state riportate quattro tabelle: le prime due per test bilaterali,  le altre due per test unilaterali.

 

tavola  dei  valori  critici  nel  test  delle  successioni

ALLA  PROBABILITA’  0.05  PER  TEST  A  DUE  CODE

La tabella superiore riporta i valori minimi e quella inferiore i valori massimi significativi.

n₂

 

n₂

tavola  dei  valori  critici  nel  test  delle  successioni

ALLA  PROBABILITA’  0.05  e  0.01  PER  TEST  A  UNA  CODA

Le tabelle riportano i valori minimi significativi.

E’ significativo ogni numero di successioni minore od uguale a quello riportato nella tabella.

 

a = 0.05

n₂

 

a = 0.01

n₂

 

Le prime due tabelle forniscono i valori critici del numero di successioni minimo e massimo alla probabilità a = 0.05; le due tabelle sono simmetriche, per cui è indifferente l’identificazione in n₁ o n₂ del numero di osservazioni di uno qualsiasi dei due gruppi.

Nella tabella superiore, è riportato il valore minimo significativo: permette di rifiutare l’ipotesi nulla, con qualsiasi valore uguale o minore di quello riportato. Qualunque valore osservato (R) che sia uguale o minore a quello riportato ha una probabilità £ 0.025 di verificarsi, nell'ipotesi che H₀ sia vera.

Nella tabella inferiore, è riportato il valore massimo significativo: permette di rifiutare l’ipotesi nulla, con qualsiasi valore uguale o superiore a quello riportato. Qualunque valore osservato (R) che sia eguale o maggiore di quello riportato corrisponde a una probabilità £ 0.025 di essere casuale.

Con i dati dell’esempio (n₁ = 8  e  n₂ = 7),

-          il valore minimo, riportato nella tabella superiore, è 4;

-          il valore massimo, riportato nella tabella inferiore, è 13.

In un test bilaterale, sarebbero quindi significativi i valori uguali od inferiori a 4 e uguali o superiori a 13: i due valori (2 e 15) del numero di successioni osservate nell’esempio con il lancio delle monete permettono di rifiutare l’ipotesi nulla.

Quando il numero di successioni è compreso nell'intervallo fra la frequenza minima e quella massima riportate della tabella, con esclusione dei valori riportati, non si è nelle condizioni di rifiutare l'ipotesi nulla H₀: la sequenza dei due eventi può essere ritenuta casuale.

 

Le altre due tabelle forniscono i valori critici per test ad una coda, al fine di verificare se il numero di successioni osservato sia minore di quello casuale, atteso nella condizione che H₀ sia vera (_r ).

La tabella superiore riporta i valori critici alla probabilità a = 0.05 e

la tabella inferiore i valori critici alla probabilità a = 0.01.

A differenza delle due precedenti, queste due tabelle non sono simmetriche:

-          n₁ è il numero di osservazioni del campione maggiore ed

-          n₂ identifica il numero di osservazioni del campione minore.

 

Per grandi campioni (n₁ o n₂ > 20) non eccessivamente sbilanciati, la distribuzione delle successioni tende ad essere asintoticamente normale. I valori critici sono pertanto forniti dalla tabella della distribuzione normale standardizzata.

I valori critici alla probabilità a = 0.05 sono rispettivamente

-          1,96 per un test bilaterale (= 0.025 nelle due code della distribuzione) e

-          1,645 per un test unilaterale (= 0.05 in una sola coda della distribuzione).

Alla probabilità a = 0.01 sono rispettivamente

-          2,576 per un test bilaterale (a = 0.005 nelle due code della distribuzione) e

-          2,33 per un test unilaterale (a = 0.01 in una sola coda della distribuzione).

 

ESEMPIO 1.  In laboratorio di analisi delle sostanze inquinanti oleose, si ha il timore che lo strumento di analisi non sia corretto; si teme che, sporcandosi con una concentrazione alta, influenzi quella successiva. Sono stati misurati in successione 16 campioni d’acqua contenenti una sostanza oleosa e sono stati ottenuti i seguenti valori di concentrazione, espressi in mg per litro:

 

 

 

Sulla base dei dati raccolti, si può affermare alla probabilità a = 0.05 che lo strumento non sia corretto?

 

Risposta.  Occorre dapprima classificare i valori in due categorie: bassi (-) e alti (+). E’ una trasformazione possibile mediante il confronto con la mediana (uguale a 51 nella serie dei dati raccolti), per cui i due gruppi avranno un numero uguale di osservazioni basse e alte (8-  e 8+).

La sequenza delle risposte, tradotte in valori bassi (-) e alti (+), diventa

 

 

 

 e risulta formata da 4 successioni.

 

Sulla base dell'ipotesi formulata, è un test ad una coda: si tratta infatti di verificare se esiste trascinamento dell’informazione e quindi se il numero di successioni sia significativamente inferiore al valore atteso, nell’ipotesi di totale casualità degli eventi come dovrebbe succedere con uno strumento corretto.

Secondo l'ipotesi nulla

 

 il numero medio di successioni osservate (R) non si discosta in modo significativo da quello atteso,

 mentre secondo l’ipotesi alternativa unilaterale

 essa è significativamente minore.

 

Con n₁ = 8  e  n₂ = 8,  tale media attesa m_r

 

 risulta uguale a 9.

 

Per verificare l'ipotesi sulla casualità della sequenza delle analisi, occorre quindi risolvere il problema statistico di conoscere la probabilità di trovare 4 successioni o un valore inferiore, quando la media attesa è 9.

La tavola dei valori critici inferiori per un test ad una coda, per n₁ = 8  e  n₂ = 8  alla probabilità a = 0.05 riporta la frequenza di 5, che è maggiore del valore di R (4) osservato.

E’ un valore significativo alla probabilità a = 0.05.

Di conseguenza, con una probabilità di errare minore di 0.05, si rifiuta l'ipotesi nulla di una casualità del numero di successioni osservate e si accetta l'ipotesi alternativa: lo strumento non è preciso, ma risente del valore di concentrazione dell’ultimo campione.

 

ESEMPIO 2.  Si vuole verificare se in un gruppo d’animali l’accesso al cibo avvenga in modo casuale oppure sia possibile ipotizzare un ordine differente: un alternarsi quasi regolare tra maschi e femmine secondo lo stato sociale delle coppie oppure a gruppi dello stesso sesso.

Un gruppo di 30 (N) animali in cattività con un’organizzazione sociale a struttura gerarchica, composto da 17 (n₁) femmine e 13 (n₂) maschi adulti, deve percorrere uno stretto corridoio per accedere al cibo. L'ordine osservato d’accesso al cibo, classificato per sesso,

è stato:

MFFMFFFMMMFMFMFFFFFMMMFMMMFFFF

 

L’ordine può essere definito casuale?

 

Risposta.  Dopo aver contato il numero di successioni (R)

(già definite come il numero di simboli identici preceduti o seguiti da simboli differenti o da nessun simbolo)

 

 

 

 

 e che risulta uguale a 14,

 aver definito N (30), n₁ (17) e n₂ (13),

 si deve calcolare la media attesa, nella condizione che H₀ sia vera.

Dalla formula generale

 si stima una media attesa

 uguale a 15,73.

L’ipotesi nulla è

 ossia che il numero medio di successioni osservate (R = 14) non si discosti in modo significativo da quello atteso (15,73), mentre l’ipotesi alternativa bilaterale

 è che esso differisca in modo non casuale.

 

Il numero osservato di successioni (R = 14) è inferiore alla media attesa (). Vi è quindi una tendenza a spostarsi in gruppi dello stesso sesso. Si tratta di valutare se tale differenza tra numero osservato e media attesa sia significativa.

Il test è bilaterale, in quanto a priori non si intendeva verificare una teoria precisa, ma solo evidenziare il comportamento degli individui esaminati.

Per 2 gruppi, di 17 e 13 dati rispettivamente, alla probabilità a = 0.05 nelle due tabelle sinottiche il valore critico inferiore è 10 ed il valore critico superiore è 22. Il numero di successioni osservato (R = 14)  è compreso in questo intervallo: si accetta l'ipotesi nulla.

In riferimento al sesso, l'accesso al cibo è avvenuto in ordine casuale.

 

Il numero di osservazioni (17 e 13) è abbastanza alto e relativamente bilanciato, tale da permettere il ricorso alla distribuzione normale, al fine di stimare una probabilità più precisa di quella fornita dalla tabella attraverso i valori critici.

Dopo aver calcolato il numero di successioni osservato (R = 14) e la media attesa (15,73) nell’ipotesi che H₀ sia vera, attraverso la formula generale

si stima la deviazione standard

 che, con i dati dell’esempio,

 =  =  = 2,64

risulta uguale a 2,64.

Attraverso R (14), m_R (15,73) e s_R (2,64)

 si stima il valore di Z

che

 = 0,6553

fornisce un valore approssimato di 0,66.

Nella tavola della distribuzione normale standardizzata, esso è associato a una probabilità (P) uguale a 0.5092 per un test bilaterale. E’ una probabilità molto alta (50,92%), indicativa di una elevata casualità del numero di successioni osservato nell’esperimento. Si accetta l’ipotesi nulla: anzi, con una probabilità P così alta, si può affermare che l’ipotesi nulla è dimostrata (anche se in teoria l’ipotesi nulla è solo rifiutata o non rifiutata, mai dimostrata).

 

ESEMPIO 3.  Si ritiene importante verificare se aumenti e diminuzioni nel tasso medio d’inquinamento giornaliero avvengono casualmente (H₀) oppure se esistono periodi di più giorni con una serie continua di valori con la stessa tendenza (H₁).

Per un periodo di 50 giorni continuativi, è stata fatta una rilevazione media del tasso d’inquinamento atmosferico. Si è anche annotato costantemente se il valore era aumentato o diminuito, rispetto al giorno precedente.

Si è osservato che in 34 casi era aumentato (+) ed in 16 era diminuito (-), con la sequenza riportata nella tabella sottostante:

 

 

Quali indicazioni è possibile dedurre?

 

Risposta.  E' un test ad una coda: si chiede di verificare se le successioni osservate (R = 16) sono in numero significativamente minore dell’atteso, se fosse vera l’ipotesi di pura casualità dei valori d’inquinamento.

Il numero di osservazioni è sufficientemente alto (N = 50;  n₁ = 16;  n₂ = 34) da permettere il ricorso alla distribuzione normale standardizzata.

Secondo l'ipotesi nulla, il numero medio atteso (m_r) è

 

 uguale a 22,76 e

 la deviazione standard (s_r) è

 uguale a 3,036.

La probabilità di trovare per caso differenze uguali o superiori a quella riscontrata tra numero di successioni osservate (R = 16) ed attese (m_r = 22,76) è fornita dalla distribuzione normale standardizzata (Z)

 il cui valore è uguale a -2,226.

Nell’area di coda unilaterale, a tale valore (arrotondato a 2,23) è associata una probabilità uguale a 0.01287 o 1,287%.

La probabilità che il numero di successioni osservate sia casuale è molto piccola, nettamente inferiore a 0.05 scelta abitualmente come probabilità critica.

Si rifiuta l'ipotesi nulla e si accetta l'ipotesi alternativa: i giorni di aumento e di diminuzione dei valori d’inquinamento atmosferico non si alternano casualmente, ma tendono a concentrarsi in serie temporali di più giorni.