|
METODI NON PARAMETRICI PER UN CAMPIONE
7.15. IL METODO DI KOLMOGOROV-SMIRNOV PER UN CAMPIONE, CON DATI ORDINALI DISCRETI E CON DATI CONTINUI
Come ripetutamente
evidenziato nel capitolo sul
c2 parlando delle condizioni di
validità, quando il numero totale di osservazioni è ridotto, convenzionalmente
inferiore a 30, e/o le frequenze attese di almeno due gruppi sono inferiori a
5, non è possibile utilizzare il test
E’ tuttavia ugualmente possibile verificare la concordanza tra fatto ed ipotesi, cioè tra una distribuzione osservata e la corrispondente attesa, ricorrendo al test per un campione di Kolmogorov-Smirnov, due matematici russi quasi coetanei, Andrei Nikolaevich Kolmogorov (1903-1987) e Nikolai Vasil’evich Smirnov (1900-1966).
Soprattutto, come
verrà evidenziato ulteriormente con una dimostrazione sperimentale semplice, il
test è più potente di quello del
Proposto da A. Kolmogorov nel 1933 per il confronto tra un campione ed una distribuzione teorica (con l’articolo in italiano Sulla determinazione empirica di una legge di distribuzione, sulla rivista Giornale dell’Istituto Italiano degli Attuari Vol. 4 pp. 1-11) di solito rettangolare o uniforme, è stato sviluppato e poi esteso al caso di due campioni indipendenti nel 1939 da N. V. Smirnov con due articoli (il primo in francese, Sur les écarts de la courbe de distribution empirique, pubblicato su Recueil Mathématiques N. S. 6:, pp. 3-26; il secondo in russo ma divulgato successivamente in inglese, On the estimation of the discrepancy between empirical curves of distribution for two independent samples, pubblicato su Bull. Moscow Univ. Intern. Ser. (Math) Vol. 2, pp.3-16).
Nel 1948 Smirnov ha fornito una tabella dei valori critici (con l’articolo in inglese Table for estimating the goodness of fit of empirical distribution, pubblicato su Ann. Math Stat. vol. 19, pp. 279-281). Successivamente, anche in tempi recenti, sono state proposte diverse altre tabelle; tra esse si distinguono per completezza dei parametri considerati quelle di A. N. Pettitt e M. A. Stephens del 1977 per dati raggruppati (The Kolmogorov-Smirnov goodness-of-fit statistic with discrete and grouped data. Technometrics Vol 19, pp. 205–210) e le proposte di H. J. Khamis del 1990 per dati continui (The d corrected Kolmogorov-Smirnov test for goodnes of fit, pubblicato su Journal Statist. Plan. Infer. Vol. 24, pp. 317- 335). Tuttavia, su vari testi di statistica applicata spesso sono utilizzate quelle proposte inizialmente. Sono più semplici anche se più approssimate.
In queste dispense sono riportate quelle proposte da L. H. Miller nel 1956 (con l’articolo Table of pencentage points of Kolmogorov statistics, pubblicato su Journal of the American Statistical Association Vol. 51, pp. 111 – 121). Proposte per una scala continua, sono utilizzate in vari testi di statistica applicata anche per dati raggruppati, a motivo della buona approssimazione che esse forniscono.
Il test di Kolmogorov-Smirnov per la bontà dell’adattamento (Kolmogorov-Smirnov goodness of fit test), per la sua ampia utilizzazione è proposto su molti testi di statistica applicata. Esso può essere utilizzato - sia per dati misurati su una scala ordinale discreta o dati continui raggruppati in classi, - sia per dati continui, che possono essere misurati con una scala di rapporti oppure a intervalli oppure ordinale.
PER DATI DISCRETI O RAGGRUPPATI Tra i testi internazionali, questo metodo è riportato in - Siegel Sidney e N. John jr. Castellan del 1988 (Nonparametric Statistics for the Behavioral Sciences, (McGraw-Hill, London), tradotto in italiano nel 1992 Statistica non parametrica 2° ed., McGraw-Hill Libri Italia, Milano, 472 pp.) - Zar Jerrold H. del 1999 (Biostatistical Analysis, fourth ed., Prentice Hall, Englewood Cliffs, New Jersey, USA, pp.663 + 203 app.) A essi si rinvia per ulteriori approfondimenti e per l’uso di tabelle dei valori critici che sono più estese di quelle riportate in queste dispense.
In questo test, si richiede una condizione aggiuntiva, rispetto al test chi quadrato: i gruppi non possono essere qualitativi, ma devono essere ordinati secondo una scala di tipo almeno ordinale. L’ipotesi nulla è ancora H0: la distribuzione osservata e quella attesa sono uguali
contro l’ipotesi alternativa H1: le due distribuzioni divergono, senza per questa indicare quale possa essere la distribuzione teorica più vicina alla distribuzione osservata.
Il confronto viene realizzato mediante il valore di massima divergenza tra le due distribuzioni cumulate. Successivamente, la tabella dei valori critici indica la probabilità di trovare una divergenza pari o superiore a quella calcolata, qualora fosse vera l’ipotesi nulla. Il test si fonda sulla logica che, se un campione fosse estratto da una determinata distribuzione teorica o attesa, la sommatoria della distribuzione osservata dovrebbe discostarsi dalla sommatoria della distribuzione attesa solo per fattori casuali, di piccola entità.
Indicando con - O(Xi) ogni valore della sommatoria dei dati osservati e con - A(Xi) ogni valore della sommatoria dei dati attesi, la deviazione massima D’ è D’ = max | O(Xi) - A(Xi)|
Per l’uso delle tabelle, come la prossima riportata, alcuni testi propongono di rendere D’ indipendente dal numero di osservazioni mediante la trasformazione D = D’ / N benché la sua significatività dipenda dalla dimensione (N) del campione.
La tavola presenta i valori critici per un test a 2 code e a 1 coda, in rapporto alla dimensione (N) del campione e al livello di significatività a prefissata.
Ad esempio, per apprenderne l’uso, alla probabilità a = 0.05 bilaterale - con 5 dati (N = 5) è significativa una differenza uguale o superiore (D ³ ) a 0,563 - con 6 dati è significativa una differenza di 0,519 - con 7 dati una differenza di 0,483, ecc. Alla probabilità a = 0.01 per un test unilaterale sono rispettivamente significativi valori di D uguali o superiori - a 0,627 (per N = 5) - a 0,577 (per N = 6) - a 0,538 (per N = 7).
La tavola riporta i valori critici fino ad N uguale a 40. Con N maggiore di 40, per test bilaterali sono significativi - alla probabilità a = 0.05 valori di
D
³ 1,36
/
- alla probabilità a = 0.01 valori di
D
³ 1,63
/
Con N maggiore di 40, per test unilaterali sono significativi - alla probabilità a = 0.05 valori di
D
³ 1,22
/
- alla probabilità a = 0.01 valori di
D
³ 1,52
/
Il ricorso al test di Kolmogorov-Smirnov permette di formare un numero molto alto di gruppi, ognuno con poche osservazioni attese, mentre il test chi-quadrato impone un loro raggruppamento, per non avere frequenze attese inferiori a 5.
Il test di Kolmogorov-Smirnov è più potente del test c2( g. d. l. ), in particolare quando il campione non è grande. Quando la numerosità del campione è grande, i due test hanno potenza simile e forniscono probabilità simili.
Per illustrane l’applicazione in modo semplice, è utile seguire un esempio in tutti i suoi passaggi logici, dalla presentazione del problema scientifico alla risposta conclusiva.
1) Si assuma che in dieci ore di osservazione, dalle ore 7 alle 17, un ricercatore di etologia abbia avvistato 15 uccelli della stessa specie dal suo luogo di appostamento, con la seguente cadenza oraria:
Egli intende verificare se - si tratta di una distribuzione approssimativamente uniforme, cioè se le differenze osservate rispetto a tale ipotesi possono essere considerate entro i limiti delle variazioni accidentali (H0), - oppure se sia più attendibile pensare ad una incidenza effettiva dell’ora sul numero di avvistamenti (H1) e quindi se le frequenze nelle diverse fasce orarie seguono una legge diversa (non nota, ma differente da quella di uniformità).
2 – La prima operazione da effettuare è la stima della distribuzione attesa, nella condizione che l’ipotesi nulla sia vera. Se l’ora non incidesse sulla frequenza di volo degli uccelli, il ricercatore avrebbe dovuto avvistarne un numero costante per ogni intervallo unitario di tempo; con 15 uccelli osservati in 5 intervalli di tempo, il ricercatore avrebbe dovuto osservarne 3 ogni 2 ore, con la seguente cadenza
Il confronto a coppie tra le due distribuzioni cumulate permette di calcolare le differenze tra coppie di frequenze e di trovare facilmente la differenza assoluta massima:
Valori critici di Dmax nel test di Kolmogorov-Smirnov per la bontà dell’adattamento con dati continui e raggruppamenti in classi Test unilaterali e test bilaterali con N da 5 a 24 (Proposti da Miller, 1956)
Valori critici di Dmax nel test di Kolmogorov-Smirnov per la bontà dell’adattamento con dati continui e raggruppamenti in classi Test unilaterali e test bilaterali con N da 25 a 40 e approssimazione per N > 40 (Proposti da Miller, 1956)
La differenza assoluta massima è 7.
3 - E’ intuitivo pensare che essa possa essere tanto più grande quanto maggiore è lo scarto tra osservato ed atteso. Ma questo valore dipende anche dal numero totale di osservazioni: la differenza massima tende ad aumentare in valore assoluto al crescere delle dimensioni del campione. Anche se la sua significatività è strettamente legata ad esso, è possibile rendere lo scarto massimo assoluto indipendente dal numero totale di osservazioni, mediante il rapporto
che, nel caso dell’esempio,
è Dmax = 0,466.
4 - Sulla tabella dei valori critici di D nel test di Kolmogorov-Smirnov per un campione in un test bilaterale, - con un’ampiezza del campione (N) pari a 15 osservazioni, - il valore critico della deviazione massima D è - 0,338 per la probabilità a = 0.05 e - 0,404 per la probabilità a = 0.01. Il valore calcolato nell’esempio (uguale a 0,466) risulta maggiore di quelli tabulati sia alla probabilità a = 0.05 che, soprattutto, a quella a = 0.01.
5 - Di conseguenza, si rifiuta l’ipotesi nulla H0, secondo la quale le variazioni sono solamente accidentali. Pertanto, implicitamente, si accetta l’ipotesi alternativa H1, secondo la quale le differenze tra distribuzione osservata e distribuzione attesa sono troppo grandi per poter essere, ragionevolmente, ritenuti casuali. Traducendo il risultato dell’analisi statistica in termini biologici, si può affermare che la specie di uccelli oggetto dell’osservazione si alzi in volo in modo preferenziale durante alcune ore del giorno.
L'analisi statistica condotta permette di evidenziare alcune caratteristiche del test.
Se nell’esperimento
durante le 12 ore d’osservazione si fossero rilevati 30 individui, il campione
sarebbe stato sufficientemente grande per ricorrere all’uso del test
Tuttavia, per rispettare anche la condizione di avere in ogni casella un valore minimo di osservazioni non inferiore a 5, sarebbe stato necessario raggruppare le osservazioni di classi adiacenti. E’ un’operazione che - da una parte permette di rispettare le condizioni di validità; - ma dall'altra determina una perdita d’informazione sulle differenze tra le varie ore.
Il test di Kolmogorov-Smirnov permette di suddividere il tempo in un numero molto più grande di gruppi: con un’analisi più dettagliata, evidenzia differenze che con il raggruppamento tendono a scomparire. Inoltre, il raggruppamento in classi, per ridurre il numero di gruppi, può contenere una dose elevata di soggettività, determinando differenze tra le due cumulate che variano in rapporto al numero e al tipo di classi formate.
Un altro problema importante è distinguere se il test è a una coda oppure a due code. Quello espresso in precedenza, nella quale non veniva indicata la direzione della differenza per un’ora o un gruppo di ore specifiche, era un test bilaterale. Se l’ipotesi alternativa all’ipotesi di uniformità fosse stata che al mattino il numero di avvistamenti è minore di quello pomeridiano, l’ipotesi sarebbe stata unilaterale. In questa scelta, occorre porre estrema attenzione al fatto che l’ipotesi non può essere formulata osservando i dati, ma deve essere esplicitata a priori.
Come già citato, nel 1977 A. N. Pettitt e M. A. Stephens hanno proposto tabelle di valori critici che dipendono anche dal numero di gruppi e dal numero di dati. Per dimostrare il loro uso e presentare un ulteriore esempio di applicazione di questo test per risposte ordinali raggruppate, si assuma di voler valutare il livello di gradimento di un cibo o un farmaco, sulla base della quantità crescente di una sua componente, come un dolcificante o un semplice eccipiente.
A questo scopo, a 35 pazienti sono state fatte assaggiare 5 confezioni, indicate con colori. Essi dovevano indicare solamente la confezione più gradita. Riordinati i dati sulla base della quantità della sostanza contenuta nelle confezioni sottoposte a giudizio, dalla quantità minore (indicata nella tabella con 1) a quella maggiore (indicata con 5) il numero di preferenze dei 35 pazienti è stata (riga 2)
1 – Per valutare se la distribuzione si allontana dalla casualità, che in questo caso richiede una distribuzione uniforme o rettangolare, prima si stima la frequenza attesa nella condizione che l’ipotesi nulla di uniformità (H0) sia vera: con 35 casi, sono 7 per ogni confezione (riga 3)
2 – Successivamente si calcola la distribuzione cumulata di quella osservata (riga 4) e la distribuzione cumulata di quella attesa (riga 5), determinando la differenza assoluta per ogni gruppo (riga 6).
3 – La differenza
massima ( Con k = 5 e N = 35, alla probabilità a = 0.05 bilaterale esso risulta 7, come quello trovato. Ne consegue che, se fosse vera l’ipotesi nulla, la probabilità P di trovare per caso tale differenza massima è inferiore 0.05 (P < 0.05). E’ una probabilità che permette di rifiutare l’ipotesi nulla: la distribuzione delle frequenze dei gradimenti è significativamente differente da una distribuzione rettangolare.
La lettura delle ultime tabelle evidenzia come molte probabilità a abbiano la stessa differenza massima, ovviamente a parità di numero di classi (k) e di numero di dati (N). La causa è che, con pochi dati, la distribuzione è discreta. Per la significatività deve essere scelta la probabilità a minore.
Valori critici di dmax nel test di Kolmogorov-Smirnov per la bontà dell’adattamento con dati discreti o raggruppati proposti da Pettitt e Stephens (1977) in test bilaterali in frequenze attese uguali o moderatamente differenti
Valori critici di dmax nel test di Kolmogorov-Smirnov per la bontà dell’adattamento con dati discreti o raggruppati proposti da Pettitt e Stephens (1977) in test bilaterali in frequenze attese uguali o moderatamente differenti
Valori critici di dmax nel test di Kolmogorov-Smirnov per la bontà dell’adattamento con dati discreti o raggruppati proposti da Pettitt e Stephens (1977) in test bilaterali in frequenze attese uguali o moderatamente differenti
Valori critici di dmax nel test di Kolmogorov-Smirnov per la bontà dell’adattamento con dati discreti o raggruppati proposti da Pettitt e Stephens (1977) in test bilaterali in frequenze attese uguali o moderatamente differenti
Valori critici di dmax nel test di Kolmogorov-Smirnov per la bontà dell’adattamento con dati discreti o raggruppati proposti da Pettitt e Stephens (1977) in test bilaterali in frequenze attese uguali o moderatamente differenti
Valori critici di dmax nel test di Kolmogorov-Smirnov per la bontà dell’adattamento con dati discreti o raggruppati proposti da Pettitt e Stephens (1977) in test bilaterali in frequenze attese uguali o moderatamente differenti
Sebbene i gruppi siano di tipo ordinale e non qualitativi, con gli stessi dati è possibile stimare il valore del c2.
Con la formula
applicata alle frequenze riportate in tabella
si ottiene c2 = 9,143 totale, con gdl = 4. Nella tavola dei valori critici del c2 con gdl = 4 - alla probabilità a = 0.10 il valore critico è 7,779 - alla probabilità a = 0.05 il valore critico è 9,488 Il valore calcolato è minore di quello critico per la probabilità a = 0.05; quindi non è possibile rifiutare l’ipotesi nulla, contrariamente a quanto concluso in precedenza. E’ una dimostrazione molto semplice della diversa potenza e della necessità di utilizzare sempre il test più potente, ovviamente nel rispetto delle condizioni di validità. Tuttavia le probabilità P non è molto differente. All’aumentare di N, le due stime convergono.
PER DATI CONTINUITra i testi internazionali, è riportato in quelli di - Hollander Myles, Wolfe Douglas A., 1999, Nonparametric Statistical Methods, 2nd ed. John Wiley & Sons, New York, 787 pp. - Sprent P., 1993, Applied nonparametric statistical methods, 2nd Edition, Chapman & Hall, London. - Zar Jerrold H. del 1999 Biostatistical Analysis, fourth ed., Prentice Hall, Englewood Cliffs, New Jersey, USA, pp.663 + 203app. A essi si rinvia per ulteriori approfondimenti e tabelle dei valori critici più estese.
Il test è utile in studi sulla sopravvivenza dopo un’operazione, in tossicologia dopo la somministrazione di un principio attivo, in etologia quando si valuta il tempo di comparsa di una reazione a uno stimolo, quando il tempo è valutato in modo continuo, senza quindi la comparsa di ties. Un numero molto limitato di ties è tuttavia accettabile. Anche in questo caso, il metodo è illustrato l’applicazione a un esempio.
Si assuma che a 20 cavie sia stato somministrato un principio attivo e che esse siano state poste sotto osservazione continua per sei giorni, misurando il tempo di comparsa del sintomo in ore, tradotte con approssimazione in decimi di giorno. Si vuole valutare se la probabilità di comparsa è costante o uniforme nel tempo.
1- La prima
elaborazione dei dati osservati
2 – La seconda operazione da effettuare è la trasformazione dei dati rilevati in valori relativi (vedi colonna 3). Poiché il tempo dell’esperimento è 6 giorni - il primo individuo che ha avuto la comparsa dopo giorni 0,6 ha un valore relativo di 0,10 (0,6/6) - il secondo con 0,8 giorni ha un valore relativo di 0,13 (0,8/6).
3 – La stessa operazione deve essere fatta per le frequenze attese. Con 20 osservazioni in 6 giorni, se la distribuzione fosse stata uniforme nel tempo (H0 vera), si sarebbe osservato un nuovo caso ogni ventesimo del tempo totale, cioè 0,05. Nella colonna 4 sono riportati i valori cumulati. Il ties comporta maggiore attenzione in questo calcolo semplice
4 – Per ogni coppia di frequenze cumulate (Osservata – Attesa) si calcola la differenza, come riporta in colonna 5.
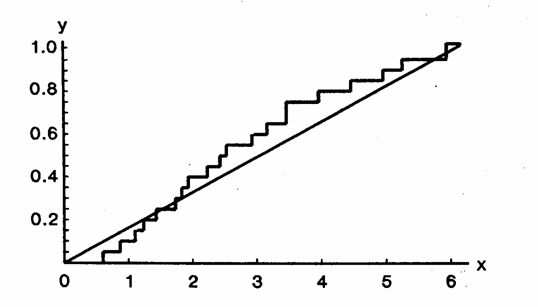
La rappresentazione grafica, nella quale in ascissa è riportato la cumulata dei valori osservati (X) e in ordinata la frequenza cumulata attesa (Y), evidenzia la differenza tra le due distribuzioni.
5 – La differenza
massima relativa D è 0,18 corrispondente alla osservazione
Sulla tabella dei valori critici di Miller, per un test bilaterale con N = 20 alla probabilità a = 0.05 il valore riportato è 0,294. Il valore calcolato è minore, quindi non sui può rifiutare l’ipotesi nulla in quanto P > 0.05.
Il test poteva anche essere impostato con ipotesi alternativa unilaterale. Ad esempio, si poteva supporre che nei primi giorni, dato il tempo richiesto dalla prima comparsa dei sintomi, le frequenze osservate fossero minori di quelle attese, rispetto a una ipotesi di distribuzione rettangolare o uniforme. Il grafico mostra che i dati osservati sono in accordo con questa attesa teorica; ma lo scarto massimo di quella zona (+0,05) è nettamente inferiore al valore critico per un test unilaterale. Infatti nella tavola dei valori critici di Miller, per un test unilaterale con N = 20 alla probabilità a = 0.05 il valore riportato è 0,265. Non è dimostrata una differenza unilaterale dall’atteso.
Il test di Kolmogorov-Smirnov può essere utilizzato per verificare l’accordo di una distribuzione sperimentale con qualsiasi distribuzione, compresa la distribuzione normale. La metodologia è leggermente modificata e i valori critici sono differenti. Per questa specifica applicazione, è utile il test proposto da H. W. Lilliefors nel 1967, modificando il test di Kolmogorov-Smirnov come dichiara appunto il titolo del suo articolo (On the Kolmogorov – Smirnov test for normality with mean and variance unknown, pubblicato su Journal of the American Statistical Association Vol. 62, pp.399 – 402).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||