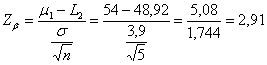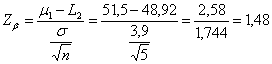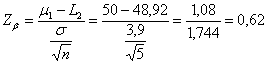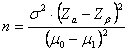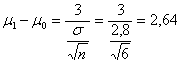VERIFICA DELLE IPOTESITEST PER UN CAMPIONE SULLA TENDENZA CENTRALE CON VARIANZA NOTAE TEST SULLA VARIANZA CON INTERVALLI DI CONFIDENZA
4.5. CALCOLO DELLA POTENZA, DEL NUMERO MINIMO DI DATI E DELLA DIFFERENZA MINIMA IN TEST PER UN CAMPIONE, CON LA DISTRIBUZIONE Z
I concetti illustrati nel paragrafo precedente, 1 - sulla potenza del test (1 - b), 2 - sul numero
minimo di dati ( 3 - sulla differenza
minima teorica (d) tra una media campionaria ( in riferimento a un campione e con l’uso della distribuzione normale (Z), quindi con varianza (s2) nota, possono essere quantificati con precisione. Un modo didatticamente semplice e che ne favorisce le applicazioni a casi reali è la dimostrazione con una serie di esempi, sviluppati in tutti i passaggi logici e metodologici. Con essi saranno illustrati gli elementi più importanti di questi tre argomenti.
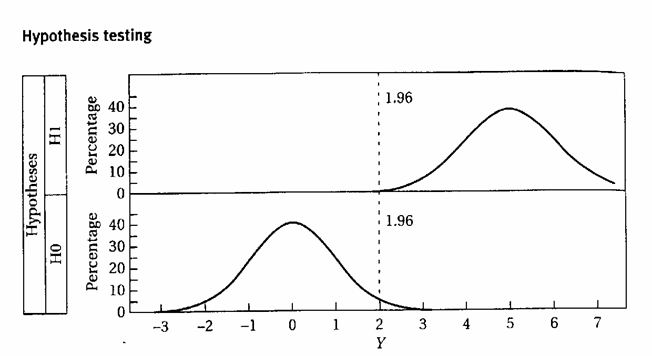
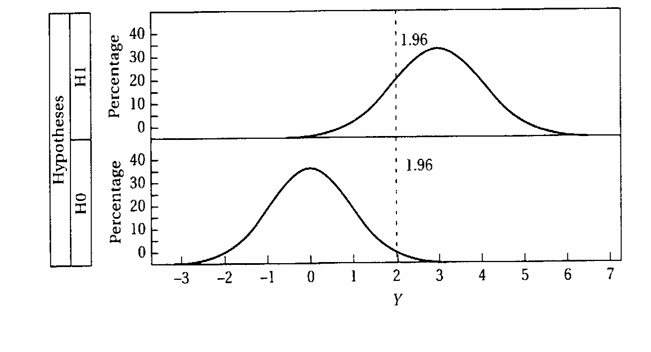
ESEMPIO 1. (CALCOLO DI b CON LA NORMALE) I concetti relativi ai fattori che determinano la potenza (1-b) di un test possono essere meglio spiegati con l’illustrazione grafica sottostante.
Per facilitarne la comprensione, è utile scomporre i diversi passaggi logici in tre parti.
I Parte - Dapprima si supponga che la quantità di principio attivo immesso in un farmaco sia m0 = 100, come dichiarato dall’azienda. (Nella parte inferiore della figura precedente è riportato 0, sia per semplificazione, sia per indicare che la differenza tra valore reale e valore dichiarato è 0). E’ ovvio che, a motivo delle variazioni non controllate nella produzione (quali differenze di temperatura ambientale, densità del farmaco, ecc.), non tutte le fiale prodotte saranno identiche e quindi non sempre la quantità immessa sarà uguale al valore 100 dichiarato. Di conseguenza,
neppure le medie In accordo con
l’ipotesi H0, la distribuzione delle medie campionarie Di essa è possibile calcolare i limiti dell’intervallo di confidenza.
Supponendo che - la deviazione standard delle fiale prodotte sia s = 2,8 - da questa
popolazione sia stato estratto un campione di dimensione - la probabilità prefissata sia a = 0.05 l’intervallo di confidenza o intervallo fiduciale bilaterale risulta
Con probabilità
pari a 0.95 ( - il limite inferiore -2,24 e - il limite superiore +2,24 intorno a m0 = 100. Si può anche
dedurre che un campione di Quindi statisticamente non è differente da essa, in un test bilaterale.
II Parte - Ora si assuma invece che, benché la ditta dichiari come prima m0 = 100, la quantità reale di principio attivo immesso, nota solo alla ditta, sia m1 = 103. Il ricercatore deve scoprire con un’analisi se la quantità immessa - è effettivamente quella dichiarata (H0 vera e quindi m0 = 100) - oppure probabilmente è differente (H1 vera e quindi una quantità m ¹ m0), - utilizzando un test bilaterale, poiché, in questo esempio, si ignora se la quantità effettiva immessa sia maggiore o minore di quella dichiarata. Anche in questo caso, non tutte le fiale saranno identiche e non tutte le medie estratte da questa popolazione saranno uguali a m1 = 103. (Questa nuova distribuzione delle medie campionarie è descritta nella parte superiore della stessa figura, intorno a 3).
Se questa distribuzione ha gli stessi parametri della precedente, quindi - la deviazione standard delle fiale prodotte è s = 2,8 - da questa
popolazione è stato estratto un campione di dimensione - la probabilità prefissata è a = 0.05 l’intervallo di confidenza o intervallo fiduciale bilaterale risulta
Le medie
campionarie
III Parte. Estraendo da
questa seconda popolazione (con m1 = 103) una confezione di
6 fiale, per solo effetto delle variazioni casuali la media campionaria Infatti, - se la media campionaria estratta dalla popolazione è più vicina a 100 di 102,24 - che rappresenta il limite superiore della distribuzione normale con media m = 100, - dovremmo concludere che potrebbe essere una sua variazione casuale, con probabilità 1 - a. Quindi, accetteremmo l’ipotesi nulla (H0: m = 100) e non saremmo in grado di affermare che proviene da una popolazione con m diversa.
Commetteremmo un errore di II Tipo. Questo rischio è b. Il suo valore è dato da Zb =
si ottiene Zb = il risultato di Zb uguale a –0,67. In una tavola normale unilaterale a Zb = 0,67 corrisponde una probabilità b = 0,251. Si deve concludere che la potenza (1-b) di questo test è uguale a 0,749 (1 - 0,251). Spesso è espresso in percentuale: 74,9%.
Come già
evidenziato, l’errore è commesso solo da una parte, poiché si ha errore
solo quando il valore medio Ritornando ai concetti illustrati all’inizio del paragrafo, ora con i passaggi logici illustrati è semplice capire che - scegliendo una probabilità a maggiore, - diminuendo s, - aumentando - accrescendo d, diminuisce la probabilità b e quindi aumenta la potenza (1-b) del test.
ESEMPIO 2. (CON UNA DIFFERENZA d MAGGIORE) Se a parità di tutti gli altri fattori considerati, come nella figura successiva in cui la distribuzione normale superiore è simmetrica intorno a 5, la m reale dell’ipotesi alternativa H1 fosse stata uguale a m = 105, il valore di Zb sarebbe risultato Zb = uguale a 2,40.
Quindi dalla tabella dei valori critici unilaterali si sarebbe ricavata una probabilità b = 0.008 (0,8%) e una potenza (1-b) pari a 0,992 (99,2%).
ESEMPIO 3. (Tratto,
con modifiche, da p. 166 del testo di R. Sokal e J. Rohlf del
1995 Biometry (3rd ed. W. H. Freeman and
Company, New York, XIX + 887 p.). Calcolare il rischio b dei vari test di
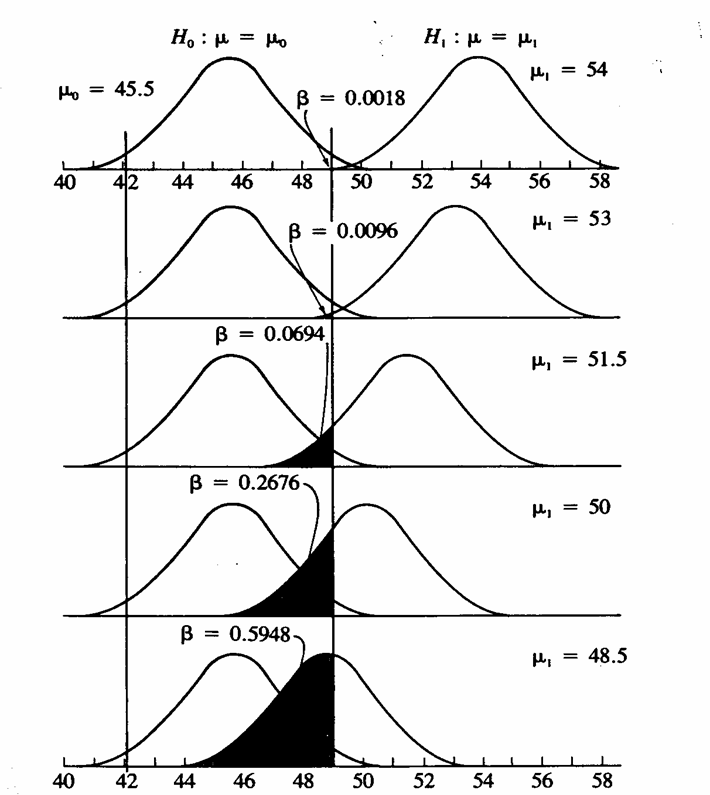
confronto tra Risposta. Per calcolare i 5 valori di b riportati nel grafico,
1 - dapprima si
devono quantificare i valori rappresentati dalle due rette parallele,
che delimitano l'intervallo di confidenza dell'ipotesi nulla H0
con media
2 - Per mediante
si ottengono il limite
inferiore
3 –
Successivamente, considerato che il valore di Con
si ottiene Nella distribuzione normale unilaterale a essa corrisponde la probabilità P = 0,0018. E' il valore di
4 - Con i valori la figura con
si ottiene Nella distribuzione
normale unilaterale a essa corrisponde la probabilità P = 0,0694 come
il valore di
Valori di
5 - Per la figura
con
si ottiene Nella distribuzione
normale unilaterale a essa corrisponde la probabilità P = 0,0694 come il
valore di
6 - Nell’ultima
figura con Con la procedura utilizzata fino a ora, si deve calcolare la quota aggiuntiva a 0,5. Con la solita impostazione
si ottiene Nella distribuzione normale unilaterale - a - a Tale probabilità è da aggiungere a 0,5 ottenendo P = 0,5948 come riportato nell’ultima figura.
Avvicinando sempre
più la media I calcoli devono
essere fatti non più rispetto a
Il valore 1 - b è chiamato potenza
a posteriori. Di norma, quando il test non risulta significativo, serve
per valutare quale poteva essere la probabilità di rifiutare l’ipotesi nulla,
sulla base dei parametri (
Spesso, quando si
programma un esperimento, a partire dai quattro parametri ( E’ la dimensione minima di un campione, per la stima della quale si deve prefissare - uno specifico
livello di significatività a, da cui dipende - la direzione
dell’ipotesi da verificare, da cui dipende ancora - un errore
campionario, cioè - la differenza d che si vuole dimostrare significativa, determinata dalla differenza tra m0 e m1. Tale quantità minima è ricavata dalla relazione
ESEMPIO 4.
(CALCOLO DEL NUMERO MINIMO) Stimare quanti dati ( - con un esperimento in cui s2 = 80 - effettuando un test bilaterale a un livello di significatività a = 0.05 (Za = 1,96) - e con una potenza dell'80% (b = 0.20 e quindi Zb = 0,84 in una distribuzione unilaterale).
Risposta. Con la formula
si ottiene
una stima
Dalle varie formule utilizzate, si ricava sempre che entrano in gioco 5 fattori, legati da rapporti precisi: a, b, d, s, Conoscendone 4, si stima il quinto.
Per stimare l’errore b di un test e quindi derivare la sua potenza (1-b), sono stati proposti anche metodi grafici che rendono la stima molto semplice e rapida, anche se hanno il difetto di nascondere quali sono i fattori implicati. Le curve riportate nel grafico successivo sono specifiche per test unilaterali o bilaterali alla sola probabilità a = 0.05, effettuati su un solo campione.
La procedura è fondata su alcuni nozioni, che possono essere schematizzate in 7 punti: 1 - la media
sottesa nell’ipotesi nulla H0 (m0) è indicata con 2 - la media
indicata nell’ipotesi alternativa H1 (m1) deve essere
individuata sull’asse delle ascisse, a destra di 3 - la distanza
tra le due medie (m1 - m0) è misurata in errori standard ( 4 - se il test è bilaterale si sale perpendicolarmente fino a incontrare la linea continua, indicata con A; 5 - se il test è unilaterale destro, si sale perpendicolarmente fino a incontrare la curva tratteggiata B; 6 - se il test è unilaterale sinistro, si sale perpendicolarmente fino a incontrare la curva tratteggiata C; 7 - la proiezione di questo punto sull’asse verticale indica il valore di b.
ESEMPIO 5. (STIMA DI b CON GRAFICO E DATI DELL’ESEMPIO 1, IPOTESI BILATERALE). La distanza tra m1 = 103 e m0 = 100 misurata in
deviazioni standard ( è
Riportato sull’asse
delle ascisse del grafico a destra di - il valore 2,64 se proiettato verticalmente incontra la curva continua A in un punto - che, trasferito orizzontalmente sull’asse delle ordinate, indica b = 0,25. E’, approssimativamente, uguale al valore calcolato nell’esempio 3.
ESEMPIO 6. (STIMA DI b CON GRAFICO E DATI DELL’ESEMPIO 1, IPOTESI UNILATERALE). La distanza tra m1 = 103 e m0 = 100 misurata in
deviazioni standard è
Riportato sull’asse
delle ascisse del grafico a destra di - il valore 2,64 se proiettato verticalmente incontra la curva tratteggiata B in un punto - che, trasferito orizzontalmente sull’asse delle ordinate, indica b = 0,17.
Tradotti in
termini di potenza ( - è pari al 75% in un test bilaterale, - è pari al 83% in un test unilaterale. Per risolvere lo stesso problema può essere utilizzata anche il grafico successivo, che riporta curve di potenza valide per test o intervalli di confidenza bilaterali.
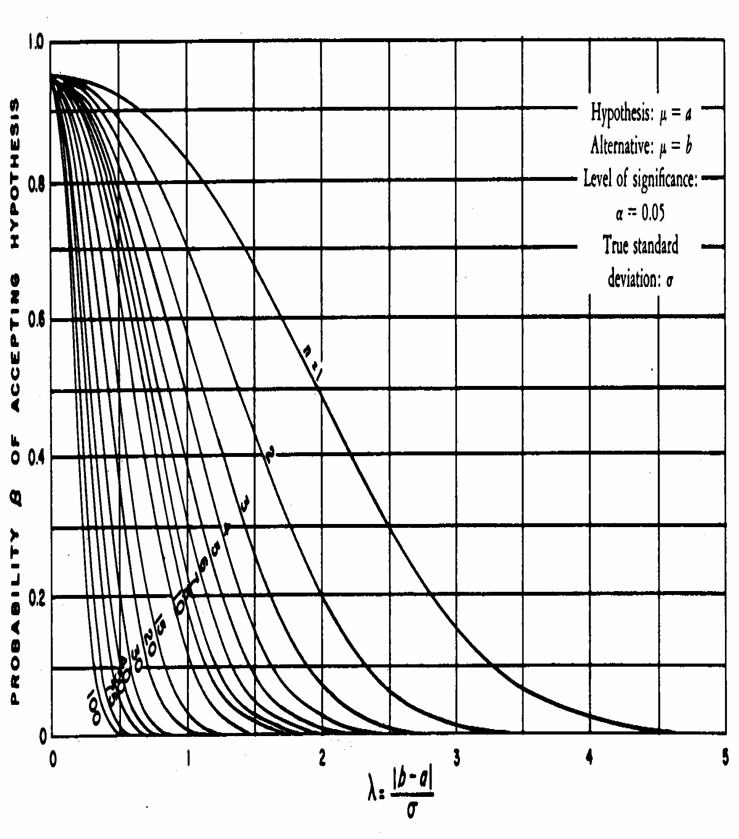
Proposta nel 1946 da C. D. Ferris, F. E. Grubbs e L. C. Weaver con l’articolo Operating Characteristics for the Common Statistical Tests of Significance (pubblicato su Annals of Mathematical Statistics Vol. 17, p. 190), la figura successiva 1 - è di uso ugualmente semplice per stimare la probabilità b, 2 – ma permette
anche di stimare
Per stimare b, nel grafico sono necessari due dati: 1) deve essere
noto 2) deve essere calcolato il parametro l attraverso la relazione
dove - - -
L’indice l è del tutto analogo all’indice f = d / s, già presentato e che sarà utilizzato in altre curve di potenza. - trasferito orizzontalmente sull’asse delle ordinate, indica il rischio b.
ESEMPIO 7 (STIMA DI b CON STESSI DATI DELL’ESEMPIO 5, MA IPOTESI BILATERALE) Con l’indice l
Individuato sull’asse delle ascisse, il valore l = 1,07 - proiettato
verticalmente incontra la curva teorica per - che, trasferito orizzontalmente sull’asse delle ordinate, indica b = 0,25.
Un valore del tutto identico, seppure sempre approssimato nella lettura grafica, a quello individuato con il grafico precedente.
Questo ultimo
grafico, come nell’esempio successivo, è utile anche per stimare le
dimensioni minime ( - attraverso il valore di l, - dopo aver prefissato il valore di b, - in un test bilaterale (per un test unilaterale serve un grafico differente, qui non riportato)
ESEMPIO 8. (CON I
DATI DELL’ESEMPIO 4, PER LA STIMA DI Stimare quanti dati
( - la differenza d = 5 è significativa, - con un esperimento in cui s2 = 80 - effettuando un test bilaterale a un livello di significatività a = 0.05 - e con una potenza dell'80% (b = 0.20).
Risposta. Da s = 8,94 con la formula
Individuato sull’asse delle ascisse, il valore l = 0,56 - incontra il valore b = 0,2 - in un punto che,
approssimativamente, è collocato a meta tra la curva per E’ un valore approssimato ma vicino a
Nel calcolo del numero minimo di dati da raccogliere, illustrato in precedenza, con l’uso della formula
in cui d = 5 si era ottenuto
per il numero
di dati da raccogliere una stima
E’ molto importante evidenziare che - per una differenza dimezzata - il numero minimo di osservazioni è moltiplicato per 4:
e quindi che - per una differenza ridotta a un quarto (d = 2,5 ), il numero minimo di osservazioni è moltiplicato per 16.
La differenza reale d (m1 - m0) è il terzo parametro che è possibile discutere - nella fase di programmazione dell’esperimento, - in quello di valutazione del risultato del test.
In un test per un campione, dopo la raccolta dei dati, d risulta significativa alla probabilità a quando d > Za - è maggiore del valore di Za - moltiplicato per l’errore standard
Ma, prima della raccolta dei dati, è necessario prendere in considerazione anche b, poiché i dati raccolti casualmente possono essere minori o maggiori della media reale. Per ottenere un test con potenza maggiore di 1-b, il valore della differenza d deve essere d ³ Zb maggiore del prodotto di Zb per l’errore
standard Da questi due concetti, per rispettare entrambe le condizioni, si deriva Za per cui il valore della differenza d d ³ (Za + Zb)
Da queste relazioni
si deducono i rapporti tra d e gli altri 4 parametri; a, b, s, In realtà, al momento di effettuare il test, il valore di d che si vuole risulti significativo deve essere scelto sulla base di conoscenze differenti dalla statistica. Esse devono essere cercate entro la disciplina nella quale si effettua la prova sperimentale e il test. Il valore d deve avere una rilevanza disciplinare, deve essere significativo per gli effetti biologici, ambientali o farmacologici che determina.
Un valore d che sia troppo piccolo - richiede un numero di dati troppo alto, - molto raramente permette un test significativo, - fornisce una risposta banale nella disciplina, in quanto irrilevante nei suoi effetti biologici, medici, farmacologi o ambientali. E solo virtuosismo statistico
I concetti generali illustrati in questo paragrafo, dell'effetto sulla potenza del test (1 - b) 1- del livello di a, 2 - delle dimensioni
del campione ( 3 - della differenza (d) che si vuole dimostrare significativa, 4 - della varianza varianza (s2), possono essere rappresentati graficamente per meglio evidenziare le loro relazioni. Le 4 figure successive, sono tratte dal testo di James E. De Muth del 1999 Basic Statistics and Pharmaceutical Statistical Applications (edito da Marcel Dekker, Inc. New York, XXI + 596 da pag. 162 a pag. 164). In un test per un campione con
è stimata la
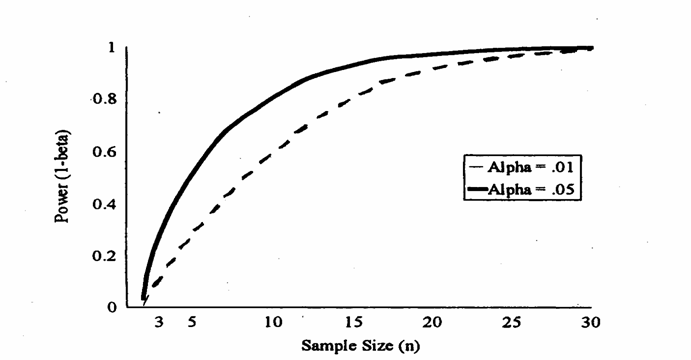
potenza Figura A. Variazioni della potenza (1-b) del test per a = 0.01 (linea inferiore tratteggiata) e a = 0.05 (linea superiore continua), all'aumentare delle dimensioni n del campione) sempre con d = 10 e s2 = 64.
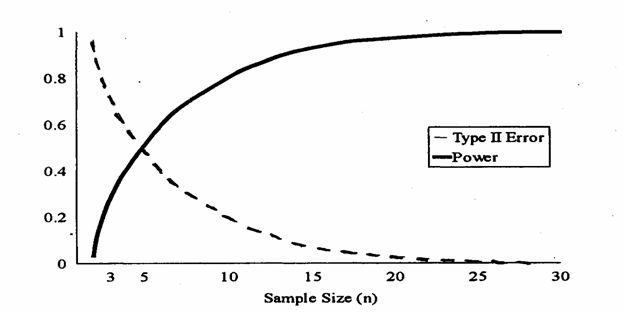
Figura B. Relazione tra la potenza 1-b (linea superiore continua) e errore di II Tipo (linea inferiore tratteggiata) all'aumentare delle dimensioni (n) del campione, sempre con a = 0.05, d = 10 e s2 = 64.
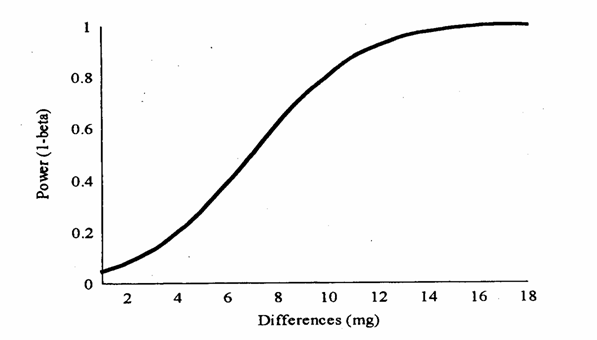
Figura C. Effetti della variazione della differenza d sulla potenza (1- b) del test, sempre con a = 0.05, n = 10 e s2 = 64
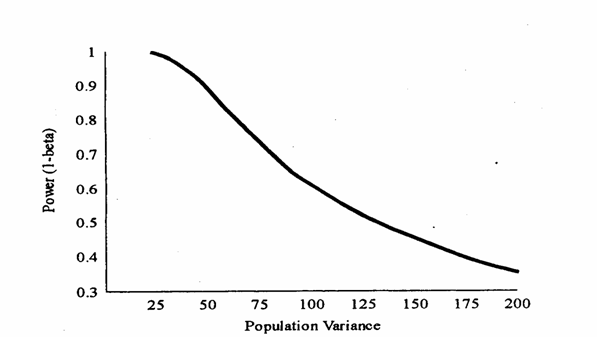
Figura D. Effetti dei cambiamenti della varianza s2 sulla potenza (1- b) del test, sempre con a = 0.05, n = 10 e d = 10.
1) Nella figura
A, sono evidenziati gli effetti sulla potenza del cambiamento delle
dimensioni 2) Nella figura
B, il concetto è più banale: all'aumentare di 3) Nella figura
C, si fa risaltare l'aumento della potenza (in ordinata) al crescere
della differenza 4) Nella figura
D, è mostrata la diminuzione della potenza all'aumentare della varianza,
diversificando
| ||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |
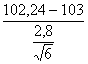 = -0,67
= -0,67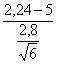 = -2,40
= -2,40