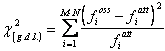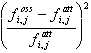CAP III - ANALISI DELLE FREQUENZE

 

 

3.9.   LE TABELLE  2 x N  CON LA FORMULA GENERALE E QUELLA DI BRANDT-SNEDECOR.  LE TABELLE  M x N

 

 

Il metodo del  per tabelle 2 x 2, con 1 grado di libertà, può essere esteso al caso generale di tabelle a due entrate, ognuna con classificazioni multiple anziché dicotomiche, con più gradi di libertà. Con l’applicazione dei medesimi concetti ed il ricorso a formule analoghe, è possibile il confronto tra M popolazioni indipendenti, per verificare l’ipotesi nulla che tutte le N percentuali o proporzioni a confronto siano uguali.

Sono le tabelle M x N in cui l’ipotesi nulla è

 

e l’ipotesi alternativa è

 = almeno una delle p è diversa dalle altre.

 

Il caso più semplice di tabelle M x N è la tabella di contingenza , per risposte dicotomiche di N gruppi a confronto. Essa ha N - 1 gradi di libertà, derivati dalla formula generale

(N-1)  (2-1)

Anche in queste tabelle, è bene evitare di avere caselle con frequenze teoriche od attese inferiori a 5, per non avere una eccessiva perdita di potenza del test. Tuttavia, la tolleranza in merito a queste condizioni di validità diviene maggiore: si accettano frequenze attese di 1 o 2, oppure un numero più alto di frequenze uguali a 4-5, poiché le variazioni casuali tendono a compensarsi.

Il c² con parecchi gradi di libertà è meno sensibile agli errori determinati da frequenze attese piccole.

 

ESEMPIO. Si vuole confrontare l’effetto di 5 pesticidi, dispersi in 5 aree diverse, sulla sopravvivenza di una stessa specie animale. I risultati ottenuti sono riportati nella tabella sottostante.

 

DISTRIBUZIONE OSSERVATA

 

 

Esiste una differenza significativa tra le percentuali (o le proporzioni) di animali morti con i vari pesticidi sperimentati?

 

Risposta.  L’ipotesi nulla è che tutti 5 i pesticidi a confronto determinino la stessa frequenza  percentuale p di  animali morti

L’ipotesi alternativa H₁ è che almeno 1 di esse sia significativamente differente dalle altre.

Dopo la formulazione delle ipotesi, il primo passo è il calcolo delle frequenze attese, nella condizione che l’ipotesi nulla sia vera.

 

Dopo aver riportato i totali marginali e quello generale, è possibile calcolare la distribuzione attesa in ogni casella, con il prodotto 

 

totale colonna x totale riga / totale generale.

ottenendo la tabella seguente

 

DISTRIBUZIONE ATTESA O TEORICA SECONDO L’IPOTESI NULLA

 

 

Nel calcolo della distribuzione attesa, risulta evidente che il numero di g. d. l. è (5-1) x (2-1) = 4, poiché, dopo che sono stati fissati i totali, solo 4 valori sono liberi di assumere qualsiasi valore.

Successivamente, mediante la formula generale

 

 

si calcola il valore del ₍₄₎, estendendo la sommatoria a tutte 10 le caselle

 

 

Il valore del  calcolato (3,926) è inferiore al valore critico (9,49) riportato nella tabella alla probabilità 0.05 e per 4 gradi di libertà.

Di conseguenza, non si può rifiutare l’ipotesi nulla: le differenze riscontrate tra valori osservati e valori attesi sono imputabili solo a variazioni casuali di campionamento.

In termini biologici, si afferma che la letalità dei 5 pesticidi a confronto non è significativamente diversa.

 

Anche per il calcolo del c²  in tabelle 2 x N sono stati proposti procedimenti abbreviati. Una formula frequentemente proposta nei testi di statistica applicata è quella di Brandt e Snedecor

 con C uguale a

 

 e dove

-          k = numeri di gruppi a confronto,

-          p_i = frequenza percentuale del carattere in esame nel gruppo i,

-          n_i = frequenza assoluta del carattere in esame nel gruppo o campione i,

-          N = numero totale di osservazioni,

-            = frequenza percentuale media di tutti i gruppi per il carattere in esame.

 

Applicata ai dati dell’esempio, è indispensabile calcolare dapprima le percentuali di ogni gruppo e la percentuale media totale, in riferimento ai morti oppure ai sopravvissuti. Nell’esempio, in analogia all’interpretazione precedente, è stata utilizzata la prima riga che riporta le frequenze degli animali morti

 

 

 e in riferimento a questi dati sono calcolati i parametri richiesti dalla formula

 

      

        ;   N = 120

      

      C = 2176,5 - 2085 = 91,5

 

Da essi si stima un valore del   

 

 che risulta uguale a 3,765

 

Si può osservare come, con la formula di Brandt e Snedecor, si ottenga un risultato (3,765) simile a quello della formula generale (3,9266), a meno delle approssimazioni necessarie nei calcoli.

La formula abbreviata semplifica i calcoli e riduce i tempi richiesti; ma per l’interpretazione del risultato è sempre utile disporre anche della distribuzione attesa, poiché i confronti tra le caselle con le frequenze assolute osservate e quelle corrispondenti con le frequenze, permettono di individuare le cause della significatività complessiva.

 

Nel caso più generale di una tabella di contingenza , il  è più frequentemente utilizzato come test per l’indipendenza tra i caratteri riportati in riga madre (di norma, i Trattamenti) e quelli riportati nella prima colonna (le Categorie). L’ipotesi nulla è che vi sia indipendenza tra tali variabili, mentre l’ipotesi alternativa bilaterale è che esista associazione. 

Anche in questo caso, in molti test di statistica applicata è sconsigliato avere caselle con frequenze attese inferiori a 5. In altri testi, si sostiene che la maggiore robustezza del chi quadrato con più gradi di libertà permette risultati attendibili anche quando si dispone di frequenze minori. Tuttavia, qualora si avessero alcune frequenze molto basse, è bene riunire questi gruppi in un numero inferiore di categorie, aggregando ovviamente in modo logico le variabili che sono tra loro più simili.

 

In una tabella di contingenza M x N, i gradi di libertà sono

x 

dove M è il numero di colonne e N è il numero di righe

Il valore del chi quadrato può essere ottenuto con la formula generale, fondata sullo scarto tra frequenze osservate e frequenze attese.

 

Anche per le tabelle  sono state proposte formule rapide, come il metodo di Skory. In realtà, sono metodi più complessi di quelli già illustrati e non presentano vantaggi apprezzabili nel tempo richiesto e nelle approssimazioni dei calcoli, rispetto alla formula generale. Inoltre, nell’interpretazione dei risultati hanno lo svantaggio di evidenziare la differenza complessiva, ma non ogni singola differenza tra la distribuzione attesa e quella osservata.

Quando si analizzano e si interpretano i risultati in tabelle M x N dopo il calcolo del c², se si è rifiutata l’ipotesi nulla non è semplice individuare con precisione a quali caselle, a quali associazioni positive o negative, sia imputabile in prevalenza il risultato complessivo. A questo scopo esistono due metodi.

Il più semplice consiste nel riportare in una tabella M x N il contributo al valore del chi quadrato fornito da ogni casella; ma è utile solo per la descrizione. Il secondo si fonda sulla scomposizione e sull’analisi dei singoli gradi di libertà, come verrà di seguito schematicamente illustrata nei suoi concetti fondamentali.

 

Il contributo al valore totale dato da ogni casella è evidenziato riportando per ognuna di essa, in una tabella M x N, il valore del rapporto

 

ESEMPIO. Si vuole verificare se esiste associazione tra tipo di coltivazione del terreno e presenza di alcune specie d’insetti. In 4 diversi appezzamenti di terreno, con coltivazioni differenti, è stata contata la presenza di 5 specie differenti di insetti, secondo le frequenze riportate nella tabella sottostante.

 

DISTRIBUZIONE OSSERVATA

 

 

 

Con questi dati raccolti in natura, si può sostenere che esiste associazione tra specie d’insetti e tipo di coltivazione del terreno?

 

Risposta.  L’ipotesi nulla afferma che il tipo di coltivazione del terreno non influisce sulla presenza delle specie d’insetti. L’ipotesi alternativa sostiene che esiste associazione tra tipo di coltivazione e presenza d’insetti, ricordando che può  esistere associazione sia quando il tipo di coltivazione aumenta la frequenza di alcune specie sia quando la riduce significativamente.

E’ un test bilaterale (i test in tabelle M x N possono essere solo bilaterali).

Se non esistesse associazione e la distribuzione delle 5 specie d’insetti nella 4 zone con coltivazioni differenti fosse uniforme, si avrebbe la seguente distribuzione attesa che ha 12 g.d.l (4 x 3).

 

DISTRIBUZIONE ATTESA O TEORICA, SECONDO L’IPOTESI NULLA

 

 

Con la formula generale, considerando le frequenze osservate e quelle attese nelle 20 caselle si ottiene un valore del chi quadrato con 12 g.d.l.  uguale a 32,251

 

 

Sia per ottenere il risultato complessivo che per la successiva interpretazione, è utile calcolare il contributo di ogni casella al valore del chi quadrato totale, utilizzando la sua proprietà additiva, come evidenzia la tabella successiva

 (OSSERVATO - ATTESO)² / ATTESO

 

 

 

Alla probabilità a = 0.05 con 12 g.d.l., la tabella del  dà un valore critico uguale a 21.03.

Il valore del  calcolato (32,251) è significativo. Si rifiuta l’ipotesi nulla ed implicitamente si accetta l’ipotesi alternativa: esistono specie che hanno una frequenza maggiore ed altre una  frequenza minore in rapporto al tipo di coltivazione.

 

Per entrare nella interpretazione più fine di questa significatività complessiva, la tabella che riporta il contributo di ogni casella al valore complessivo del chi quadrato mostra in quali associazioni tra righe e colonne si trovano gli scarti relativi maggiori tra osservati ed attesi.

Nell’esempio, una sola casella fornisce quasi la metà del valore totale: è la specie C nella coltivazione I, con un contributo di 14,315 al valore totale di 32,251. Il confronto tra valori osservati ed attesi mostra che la significatività è imputabile ad una presenza maggiore dell’atteso di individui della specie C nella coltivazione I.

La specie C e la coltivazione I formano un’associazione positiva.

Contribuisce sensibilmente al valore del chi quadrato anche una presenza più ridotta della specie D nella coltivazione I; è un’associazione negativa, che contribuisce al chi quadrato complessivo con un valore di 6,048.

 

La scomposizione dei gradi di libertà di queste tabelle complesse è un altro modo che permette di avere informazioni più dettagliate, sugli effetti di ogni particolare gruppo di dati.

La proprietà additiva del  e dei relativi gradi di libertà consente la scomposizione di una tabella  in tanti test , ognuno con 1 g.d.l., quanti sono i gradi di libertà totali della matrice.

Quando si è interessati ad individuare la causa di una significativa deviazione dall’ipotesi nulla, è possibile costruire i test che ne spiegano le quote maggiori.

 

Prendendo come schema di riferimento una teorica tabella   con la relativa simbologia

 

 

con  9 dati si ottiene un  che ha 4 gradi di libertà. Se risulta significativo, è utile scomporre questa valutazione globale, per conoscere quali confronti singoli  siano la causa di questa differenza tra frequenze osservate e frequenze attese.

Con 4 gradi di libertà è possibile fare solamente 4 confronti. Se impostati correttamente, la somma dei valori di questi 4 ₍₁₎ con 1 grado di libertà deve essere uguale al valore complessivo del con 4 g.d.l. calcolato su tutti i dati.

La ripartizione deve essere eseguita in modo gerarchico: stabilita una prima suddivisione, le ripartizioni successive devono essere attuate sempre all’interno della precedente. E’ il modo per rendere i confronti ortogonali: la conclusione precedente non deve dare informazioni sul test successivo.

Con la tabella 3 x 3 presentata, una possibile partizione dei 4 gradi di libertà è quella di seguito riportata:

 

 

 

Anche dalla semplice osservazione risulta evidente che esistono molte possibilità differenti di suddivisione della medesima tabella.

La scelta dipende dal ricercatore, che è totalmente libero di scegliere i raggruppamenti di caselle che gli sembrano più logici ed utili per spiegare la significatività ottenuta; ma tale scelta deve essere fatta “a priori” non  “a posteriori”, per non alterare la probabilità di scegliere una distribuzione casualmente significativa. Scelta a priori significa che essa deve essere fatta in modo totalmente indipendente dai dati rilevati; non è corretto individuare quali gruppi hanno le frequenze maggiori e quali le frequenze minori e successivamente pianificare la suddivisione, sulla base delle differenze osservate, scegliendo quelle che danno valori del chi quadrato maggiori.

L’argomento è complesso e l’applicazione richiede altre conoscenze, oltre a questi concetti fondamentali, adeguati al livello di conoscenze del presente manuale.

Per la scomposizione dei gradi di libertà del c² in tabelle M x N, non molto frequente nella letteratura attuale, si rinvia a testi specifici.