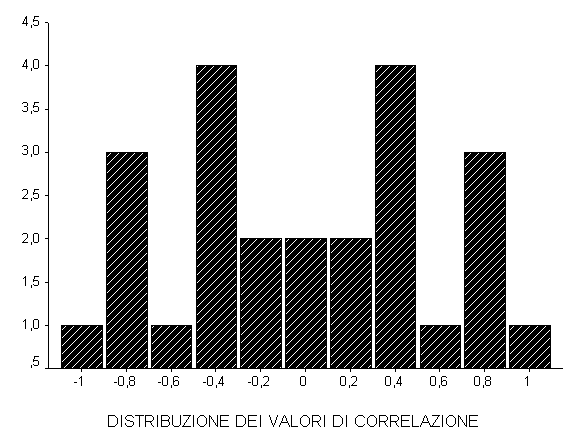TEST NON PARAMETRICI

PER CORRELAZIONE, CONCORDANZA,

REGRESSIONE MONOTONICA E REGRESSIONE LINEARE

 

 

21.4.  ALTRI METODI PER LA CORRELAZIONE NON PARAMETRICA: TEST DI PITMAN CON LE PERMUTAZIONI; TEST DELLA MEDIANA DI BLOMQVIST.

 

 

Per l’analisi della correlazione non parametrica, sono stati proposti altri metodi molto meno noti poiché riportati raramente sia nei testi di statistica applicata sia nelle librerie informatiche a grande diffusione internazionale. Di norma, sono test meno potenti del r e del t, in quanto fondati su condizioni di validità più generali; altri, in situazioni contingenti, offrono alcuni vantaggi pratici.

Nella ricerca applicata è quindi utile la conoscenza di alcuni di questi metodi.

 

Tra essi, riportati nell’ultima versione nel testo di P Sprent e N. C. Smeeton del 2001 dal titolo Applied Nonparametric Statistical Methods (Chapman & Hall/CRC, London, 461 p.) possono essere ricordati:

-  il test di Pitman, quando si dispone di un numero di dati particolarmente ridotto;

-  il test della mediana di Blomqvist, quando le due serie di misure sono approssimate o contengono valori con attendibilità differente, con tutti i vantaggi e gli svantaggi propri dei test della mediana già presentati.

 

 

 

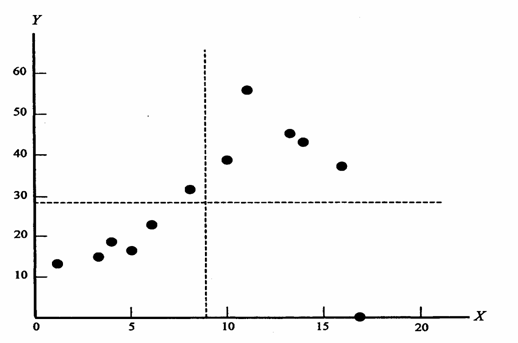
Si supponga che questo diagramma di dispersione, tratto dal testo di Sprent e Smeeton citato, sia la rappresentazione grafica del numero di errori commessi da 12 allievi impegnati prima in un compito di matematica (M) e successivamente in uno di lingua straniera (L):

 

 

 

Che tipo di relazione esiste tra le due serie di dati? Può essere vera la teoria che afferma che gli studenti migliori in matematica sono i migliori anche nell’apprendimento delle lingue?

L’interpretazione, sempre necessaria dal punto di vista disciplinare seppure non richiesta dall’analisi statistica, potrebbe essere che i migliori in matematica sono tali perché più diligenti, logici e studiosi; quindi, con poche eccezioni, anche i migliori in tutte le altre discipline, tra cui lo studio della lingua.

 

Ma può essere ugualmente convincente anche la teoria opposta.

Chi è portato alla logica matematica ha poca attitudine per l’apprendimento alle lingue; inoltre la conoscenza delle lingue straniere richiedono attività e impegni, come i viaggi, i soggiorni all’estero e i contatti con le persone, che male si conciliano con lo studio e la riflessione richiesti dalla matematica.

 

I risultati della tabella e la loro rappresentazione nel diagramma di dispersione sembrano complessivamente (all’impressione visiva che tuttavia deve essere tradotta nel calcolo delle probabilità con un test) deporre a favore della prima teoria; ma il punto anomalo, l’allievo che ha commesso più errori in matematica e nessuno in lingua, forse per condizioni familiari particolari, è un dato importante a favore della seconda teoria.

Come tutti i valori anomali, questo dato da solo sembra in grado di contraddire l’analisi fondata su tutti gli altri, almeno di annullarne le conclusioni. I metodo parametrici, che ricorrono al quadrato degli scarti, danno un peso rilevante a questi dati anomali; ma la loro presenza evidenzia una condizione di non validità di tale analisi.

 

Per quanto attiene la verifica statistica di queste teorie mediante l’analisi della regressione, i dati riportati, costruiti ad arte ma verosimili nella ricerca applicata come affermano i due autori, rappresentano un esempio didattico che bene evidenzia quattro caratteristiche dei dati, da discutere sempre nella scelta del test più adatto per analisi con la correlazione:

-  il tipo di scala,

-  la normalità della distribuzione,

-  l’omogeneità della varianza,

-  la presenza di un valore anomalo.

 

Anche questa breve introduzione evidenzia quanto sia utile avere un quadro ampio delle opportunità offerte dai test, per scegliere sempre quello con la potenza maggiore, in rapporto alle caratteristiche dei dati e nel pieno rispetto dei presupposti di validità.

 

Nel 1937, E. J. G. Pitman ha proposto un test di correlazione non parametrica (vedi l’articolo Significance tests that may applied to samples fron any population, II: The correlation coefficient test, pubblicato su Journal of the Royal Statistical Society, Suppl. 4, pp. 225-232), che utilizza il calcolo combinatorio già illustrato nei test di casualizzazione per due campioni dipendenti e per due campioni indipendenti.

Per verificare l’ipotesi nulla sulla correlazione (H₀: r = 0) contro un’ipotesi alternativa sia bilaterale (H₁: r ¹ 0), che può essere anche unilaterale in una delle due direzioni (H₁: r < 0   oppure   H₁: r > 0), propone un test esatto, fondato sulle permutazioni.

 

Sviluppando un esempio didattico con soli 4 coppie di dati,

-  dopo aver ordinato i valori della variabile X in modo crescente, come nei metodi di Spearman e di Kendall,

 

-  prende in considerazione la variabile Y, stimandone tutte le possibili permutazioni, che con n dati sono n!

Con n = 4 esse sono 4! = 24 come nella tabella successiva, nella quale sono organizzate in modo logico e con valori di r tendenzialmente decrescente.

 

 

 

Tale distribuzione può essere riassunta in una tabella, qui organizzata in modo crescente per il valore di r

 

 

 

 

(Le frequenze relative sono arrotondate alla terza cifra, affinché il totale sia 1,00)

 

 

Con la distribuzione di frequenza di tutte le permutazioni, si rifiuta l’ipotesi nulla H₀ quando la serie osservata degli Y campionari è collocata agli estremi della distribuzione, nella zona di rifiuto

Nel caso dell’esempio, se l’ipotesi alternativa fosse stata H₁: r > 0 si sarebbe potuto rifiutare l’ipotesi nulla solo se la distribuzione campionaria fosse stata quella estrema, riportata per ultima nella tabella con l'ordine crescente dei valori, cioè quella con i ranghi 1, 2, 3, 4 in ordine naturale.

 

Infatti la probabilità di trovarla per caso, nella condizione che H₀ sia vera, è P < 0.05 (esattamente P = 0.042, avendo frequenza 1/24).

La diffusione dei computer e di programmi informatici appropriati permette l’uso di questo metodo.

Con pochi dati, come con 4 ranghi, la distribuzione delle probabilità ha forma simmetrica ma non normale, evidenziata visivamente dalla figura precedente. Per un numero più alto di osservazioni, la distribuzione delle probabilità tende alla normale, ricordando che il numero delle permutazioni cresce rapidamente all’aumentare di n!

Ad esempio con 8! è già 40320 e con  10! è addirittura 3628800.

 

Nel caso qui presentato, il metodo delle permutazioni è stato applicato ai ranghi per semplicità didattica. In realtà questo test di permutazione dovrebbe essere applicato ai valori osservati, richiedendo le stesse condizioni di validità di tutti i test di permutazione, cioè la distribuzione normale dei dati. In tale condizione il valore di correlazione varia da –1 a +1 e la sua efficienza asintotica relativa o efficienza di Pitman è stimata uguale a 1. Ovviamente offre gli stessi vantaggi dei test di permutazione, con campioni piccoli:

-  la possibilità di calcolare direttamente la significatività, con un numero minimo di dati;

-  la stima delle probabilità esatte.

Per grandi campioni è inapplicabile, anche limitando l’analisi ai valori collocati nella zona di rifiuto, per il numero rapidamente crescente delle permutazioni.

 

 

Il test della mediana per la correlazione, analogo al test della mediana per due campioni, in realtà è un test di associazione; nell’articolo di presentazione, dall’autore (Blomqvist) è stato chiamato test di dipendenza tra due variabili casuali.

Il metodo è stato proposto nel 1950 da N. Blomqvist con l’articolo On a mesure of dependence between two random variables (pubblicato su The Annals of Mathematical Statistics, Vol. 21, pp. 593-600); nel 1951 è stato ripreso sulla stessa rivista in un elenco di test analoghi, nell’articolo Some tests based on dichotomization (The Annals of Mathematical Statistics, Vol. 22, pp. 362-371).

Questo test è utile in particolare quando la distribuzione dei dati si allontana dalla normalità, come nell’esempio riportato in precedenza.

 

I dati rappresentati nel diagramma di dispersione possono essere riportati in un tabella di contingenza 2 x 2, considerando

-  la collocazione dei punti sopra o sotto la mediana,

-  congiuntamente per la variabile X e la variabile Y

-  in modo da rispettare la loro collocazione grafica.

I punti del diagramma di dispersione, nel quale le due rette perpendicolari rappresentano la mediana di X e la mediana di Y, permettono di costruire la tabella 2 x 2 con facilità:

 

Dal grafico

 

 

 è semplice ricavare la tabella di contingenza 2 x 2:

 

 

 

 

Se l’ipotesi nulla H₀ fosse vera, nel grafico e nella tabella da esso ricavata, i valori della variabile X e della variabile Y dovrebbero essere distribuiti in modo indipendente; perciò avere frequenze simili nei quattro quadranti e quindi nelle quattro caselle.

La casualità della distribuzione osservata può essere verificata con il metodo esatto di Fisher.

Esso permette anche di stimare la probabilità esatta in un test unilaterale. L’uso dei computer ha esteso con facilità il calcolo a grandi campioni.

 

Riprendendo i concetti fondamentali di tale metodo applicati a questo caso, per verificare l’ipotesi

H₀: r £ 0     contro     H₁: r > 0

- dapprima si calcola la probabilità di ottenere la risposta osservata (dove il valore minimo in una casella è 1)

 

- successivamente quella delle risposte più estreme nella stessa direzione, che in questo caso è solamente una:

 

 

 

-   Infine, per semplice somma, si ricava la probabilità di avere la risposta osservata e tutte quelle più estreme nella stessa direzione (in questo caso solo una), nella condizione che H₀ sia vera

 

Con i dati dell’esempio, si ricava una probabilità totale inferiore al 5%, che indica di rifiutare l’ipotesi nulla e quindi implicitamente di accettare quella alternativa.

Se il test fosse stato bilaterale, tale probabilità dovrebbe essere raddoppiata.

 

Per le indicazioni che ne derivano sulla scelta del test più appropriato, è interessante confrontare questo risultato con quello ottenuto applicando il test r di Pearson, r di Sperman e t di Kendall agli stessi dati del grafico, cioè alla serie bivariata: 

 

 

 

Utilizzando un programma informatico a grande diffusione, sono stati ottenuti i risultati dei tre test.

 

A)  Con il test r di Pearson il valore di correlazione è risultato r = 0,373. 

In un test unilaterale, ad esso corrisponde una probabilità P = 0.116.

Non solo non permette di rifiutare l’ipotesi nulla, ma indurrebbe a ritenere che l’ipotesi nulla sia vera, dato il valore elevato della probabilità P stimata.

 

B) Con il test r di Spearman si è ottenuto un valore di correlazione  r = 0, 434.

In un test unilaterale, ad esso corrisponde una probabilità P = 0.080 che non permette di rifiutare l’ipotesi nulla.

 

C) Con il test t di Kendall si è ottenuto un valore di correlazione  t = 0, 424; più esattamente il programma riporta t_b = 0, 424.

In un test unilaterale, ad esso corrisponde una probabilità P = 0.027 che permette di rifiutare l’ipotesi nulla.

 

Questo confronto tra i tre metodi che analizzano la correlazione con gli stessi dati evidenzia la forte differenza, attesa a causa del tipo di distribuzione, tra i due test non parametrici e quello parametrico. Ma evidenzia anche una marcata differenza, inattesa anche se nota ed effetto della forte anomalia della distribuzione, tra r e t.

Purtroppo non è stato ancora proposto un metodo per raccordare logicamente due probabilità così differenti e trarne una decisione finale condivisa.

 

In conclusione, con i dati dell’esempio, il test più semplice, fondato sui segni (P = 0.04) e quindi con condizioni di validità più generali e rispettate anche in questo caso, si dimostra il più potente e il più corretto.

 

Per una esatta comprensione dei metodi e una dizione corretta delle conclusioni, è importante ricordare ancora  che i tre tipi di test verificano l’esistenza di rapporti differenti tra le due variabili. Se un test risulta significativo,

-   nella correlazione parametrica dimostra l’esistenza di una relazione lineare,

-  mentre nella correlazione non parametrica dimostra l’esistenza di una relazione monotonica;

-  con il test della mediana dimostra solamente che esiste associazione (se positiva o negativa dipende dal segno) tra valori alti e bassi delle due variabili.