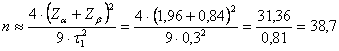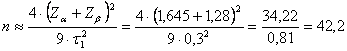TEST NON PARAMETRICI

PER CORRELAZIONE, CONCORDANZA,

REGRESSIONE MONOTONICA E REGRESSIONE LINEARE

 

 

21.3.   CONFRONTO TRA  r E t; POTENZA DEL TEST E NUMERO DI OSSERVAZIONI NECESSARIE PER LA SIGNIFICATIVITA’.

 

 

I coefficienti di correlazione non parametrica   di Spearman e  di Kendall richiedono variabili almeno di tipo ordinale. Se i valori sono misurati su una scala ad intervalli o di rapporti, le osservazioni devono essere trasformate nei loro ranghi. Anche con ranghi, è possibile calcolare il coefficiente di correlazione r di Pearson, utilizzandoli appunto al posto dei valori rilevati. E’ interessante osservare che il risultato della correlazione non parametrica r di Spearman coincide con quello ottenuto mediante il metodo r di Pearson, quando sono utilizzati i ranghi. E’ una convergenza tra test parametrico e non parametrico corrispondente, già evidenziata per altri test:

-   per l’ANOVA con la varianza non parametrica di Kruskall-Wallis,

-   per il test t di Student con il test U di Mann-Whitney.

 

Nonostante questa coincidenza dei risultati, è importante comprendere che la correlazione parametrica e quella non parametrica analizzano caratteristiche differenti della relazione esistente tra le due variabili. Mentre

-   la correlazione parametrica di Pearson valuta la significatività di una correlazione di tipo lineare,

-  la correlazione non parametrica di Spearman e di Kendall valutano l’esistenza della monotonicità; è una condizione più generale, realizzata sempre quando esiste regressione lineare.

 

In altri termini, la correlazione non parametrica

-   risulta + 1 quando all'aumentare della prima variabile aumenta anche la seconda,

-   risulta – 1 quando all’aumentare della prima la seconda diminuisce,

 ma senza richiedere che tali incrementi siano costanti, come per la retta.

 

Con termini più tecnici, il concetto è che

-  se due variabili hanno una regressione monotonica,

-  i loro ranghi hanno una relazione lineare.

 

Il testo di W. J. Conover del 1999 (Practical nonparametric statistics, 3^rd ed. John Wiley & Soons, New York, 584) mostra il diagramma di dispersione e il tipo di relazione tra le due variabili nella seguente serie di valori

 

Curva di regressione monotonica con i dati osservati

 

 

Nella tabella e nel grafico,

-  in 17 contenitori e con una osservazione della durata di 30 giorni,

-  X è la quantità di zucchero aggiunta al mosto d’uva,

-  Y è il numero di giorni dopo i quali ha avuto inizio la fermentazione.

Nelle tre quantità minori, (cioè con X uguale a 0 poi  0,5 e 1,0) la fermentazione non aveva ancora avuto inizio dopo 30 giorni di osservazione (> 30).

 

Con i dati originali, riportati nella tabella e nel grafico, per utilizzare la correlazione r di Pearson

-  un primo problema è rappresentato dalla presenza di dati stimati con approssimazione, addirittura troncati “censored” come >30, per cui non è possibile il calcolo né delle medie né della codevianza e delle devianze;

-  il secondo problema è una linearità dei dati molto approssimata, come la rappresentazione grafica evidenzia visivamente.

 

Quando al posto dei valori si utilizzano i ranghi relativi (nella tabella successiva i valori precedenti sono stati trasformati in ranghi)

 

 

 la rappresentazione grafica evidenzia la differente distribuzione lineare dei punti

 

DISPOSIZIONE DEI PUNTI E RETTA DI REGRESSIONE OTTENUTA CON LA TRASFORMAZIONE DEI DATI IN RANGHI

 

Questi concetti, come calcolare i punti della curva segmentata della figura precedente e come calcolare la retta con in ranghi in quella sovrastane sono sviluppati nel paragrafo dedicato alla regressione monotonica di Iman-Conover.

 

Per quanto attiene la potenza dei due test, il  di Spearman e il  di  Kendall hanno la stessa potenza nel rifiutare l'ipotesi nulla, anche se i valori di  e  sono numericamente differenti per lo stesso campione di dati.

Stime dell’efficienza asintotica relativa di Pitman per il test t di Kendall, ovviamente rispetto al test parametrico r di Pearson e nel caso che l’ipotesi nulla sia vera, riportano che;

-  quando la distribuzione dei dati è Normale, la potenza del t è uguale a 0,912 (3/p)²;

-  quando la distribuzione dei dati è Rettangolare, la potenza del t è uguale a 1;

-  quando la distribuzione dei dati è Esponenziale Doppia, la potenza del t è uguale a 1,266 (81/64).

 

Quando l'ipotesi nulla H₀ è vera, le probabilità a fornite dai due metodi sono molto simili; per grandi campioni distribuiti normalmente, esse tendono ad essere molto simili.

Ma quando l'ipotesi nulla H₀ è falsa, quindi si accetta come vera l'ipotesi alternativa H₁, i due differenti indici sono diversamente sensibili alle distorsioni determinate dal diverso campo di variazione (questi concetti sono sviluppati nel capito della correlazione parametrica e dell’intervallo di confidenza di r); di conseguenza, i risultati tendono a differire maggiormente.

 

Con i dati dell’esempio utilizzato nel paragrafo precedente, per un test unilaterale

-    con il   di Spearman  è stato ottenuto un valore di Z = 2,62 corrispondente alla probabilità a = 0.0044

-   con il   di Kendall  è stato ottenuto un valore di  Z = 2,93  che corrisponde a una probabilità a = 0.0017.

La differenza tra le probabilità stimate con i due diversi indici è in assoluto inferiore al 3/1000 e quindi oggettivamente molto limitata; ma è elevata (2,59 a 1), se considerata in rapporto alle piccole probabilità stimate. E’ uno dei problemi che si pone nella valutazione dei risultati: se è più corretto fornire una stima in termini assoluti oppure in termini relativi.

Per il confronto tra r e t, al momento non è noto quale indice in generale dia il valore più corretto.

 

Quanti dati è necessario raccogliere perché una regressione non parametrica sia significativa?

 

Secondo la proposta di G. E. Noether del 1987 (vedi articolo Sample size determination for some common nonprametric tests, su Journal of the American Statistical Association Vol. 82, pp. 68-79),  riportata nel testo di P. Sprent e N. C. Smeeton del 2001 (Applied nonparametric statistical methods, 3^rd ed. Chapman & Hall/CRC, 461 p.) e in quello di M. Hollander e D. A. Wolfe del 1999 (Nonparametric Statistical Methods, 2^nd ed., New York, , John Wiley & Sons) una stima approssimata del numero (n) di dati necessari affinché un valore t₁ di correlazione non parametrica sia significativo alla probabilità a e con rischio b

 è data dalla relazione

 dove

-  t₁ è il valore di t che si vuole risulti significativo rispetto all’ipotesi nulla H₀: t = 0

-  a è la probabilità o rischio di I Tipo, scelta per il test, la cui ipotesi alternativa può essere bilaterale oppure unilaterale

-  b è la probabilità o rischio di II tipo di non trovare una differenza che in realtà esiste,

-  ricordando che, per prassi  e in accordo con l’indicazione di Cohen, la probabilità b è scelta con un rapporto di circa 5 a 1 rispetto a a.

 

 

ESEMPIO  (CON TEST BILATERALE). Una analisi preliminare di una serie di rilevazioni ha permesso di stimare un valore di correlazione non parametrica t = 0,3.

Quanti dati (n) occorre raccogliere perché tale valore risulti significativamente differente da 0, in un test bilaterale alla probabilità a = 0.05 e con un rischio b = 0.20 (quindi con una potenza 1 - b = 0.80)?

 

Risposta. Dalla tabella della distribuzione normale, si ricava

-  per a = 0.05 bilaterale, Z_a = 1,96

-  per b = 0,20 (sempre unilaterale), Z_b = 0,84

 

Da essi risulta che

 

 

 che il numero di dati necessario è almeno 39.

Per rifiutare l’ipotesi nulla H₀: t = 0 ed accettare implicitamente l’ipotesi alternativa bilaterale H₁: t ¹ 0 alla probabilità a = 0.05 e con una potenza 1-b = 0.20, con t₁ = 0,3 servono almeno 39 osservazioni.

 

 

ESEMPIO  (CON TEST UNILATERALE). Nell’esempio precedente, quanti dati è necessario raccogliere se il test che si vuole utilizzare è unilaterale?

 

Risposta.   Dalla tabella della distribuzione normale, si ricava

-  per a = 0.05 unilaterale, Z_a = 1,645

-  per b = 0,20 (sempre unilaterale), Z_b = 0,84

 

Da essi risulta che

 

 

 che il numero di dati necessario è almeno 31.

 

Se la potenza (1 - b) è 0.90, quindi con b = 0.10 il cui valore di Z_b = 1,28  il numero minimo di dati necessari

 

 diventa n ³ 43.