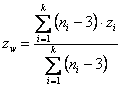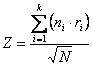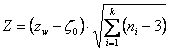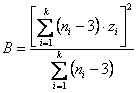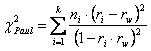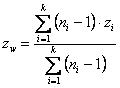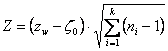CORRELAZIONE  E  COVARIANZA

 

 

18.8.   TEST PER LA DIFFERENZA TRA PIU’ COEFFICIENTI DI CORRELAZIONE  COEFFICIENTE DI CORRELAZIONE COMUNE  r_w E SUA SIGNIFICATIVITA’

 

 

Per il confronto simultaneo tra più coefficienti di correlazione indipendenti r₁, r₂, …, r_k, cioè per verificare l’ipotesi nulla

H₀: r₁ = r₂ =     = r_k

(seguendo le indicazioni di Jerrold H. Zar nel suo test del 1999 Biostatistical Analysis, fourth ed. Prentice Hall, New Jersey, pp. 390-394)

 si stima un valore  con gdl k-1

dove

-   k è il numero di coefficienti di correlazione campionari r a confronto simultaneo

-   n_i è il numero di dati campionari di ogni r_i

-   z_i è il valore di ogni r_i trasformato nel corrispondente valore z_i con la formula

 

 

 

Se il test non risulta significativo, si può concludere che i diversi valori r_i sono stime campionarie dello stesso valore reale r; di conseguenza, come sua stima migliore, è utile calcolare il coefficiente di correlazione comune o medio ponderato r_w (common r or weighted mean of r)

con

 

Successivamente, per un confronto con gli r₁, r₂, …, r_k originali, z_w può essere ritrasformato nella scala r (ricordando ancora che, in valore assoluto, r varia da 0 a 1, mentre z varia da 0 a ¥)

attraverso

 dove

-  e è la costante neperiana (approssimata con 2,718).

 

A questo valore comune r_w , con un test molto più potente rispetto a quelli di ogni singolo r_i , poiché ha il vantaggio di essere calcolato su tutte le N coppie di dati,

 in quanto

 

 può essere applicato

-   sia il test per la verifica dell’ipotesi nulla

H₀: r = 0

 che r_w non sia significativamente differente da zero

 mediante la formula proposta da J. Neyman nel 1959 (vedi capitolo: Optimal asymptotic test of composite hypothesis, pp. 213-234. Nel libro di U. Grenander (ed.) Probability and Statistics: The Harald Cramér Volume, John Wiley, New York) e ripresa da S. R. Paul nel 1988

 

 

-   sia il test per la verifica dell’ipotesi nulla

H₀: r = r₀

 che r_w non sia significativamente differente da un valore prefissato r₀

 mediante la formula proposta da S. R. Paul nel 1988 (vedi, anche per la citazione precedente, l’articolo: Estimation of and testing significance for a common correlation coefficient. sulla rivista  Communic. Statist. - Theor. Meth. 17: 39-53, nel quale fa una presentazione e una disamina generale di questi metodi)

 

 dove

-    è il valore r_w dopo trasformazione di Fisher,

-    è il valore atteso o di confronto r₀ dopo trasformazione di Fisher.

 

In questi due test sul coefficiente comune r_w , le ipotesi alternative H₁ possono essere bilaterali oppure unilaterali. L’unica differenza consiste nella stima della probabilità a: se in una distribuzione normale bilaterale oppure unilaterale.

 

Se i k campioni a confronto sono dipendenti, quali ad esempio i valori r_i di correlazione della variabile X_A con le variabili X_B, X_C, X_D calcolati sugli stessi prelievi, questa tecnica non è corretta. Si dovrà ricorrere alla statistica multivariata, con la correlazione multipla.

 

 

ESEMPIO 1.   In una ricerca sulla correlazione lineare semplice tra le quantità di due conservanti X_A e X_B contenuti in campioni di alimenti, con tre verifiche indipendenti sono stati ottenuti i seguenti risultati:

1 - r₁ = 0,48    con    n₁ = 120

2 - r₂ = 0,31    con    n₂ = 100

3 - r₃ = 0,48    con    n₃ = 150

Con questi dati,

a)   verificare se tra questi r_i esiste una differenza significativa;

b)   in caso di non rifiuto della ipotesi nulla, calcolare il coefficiente comune r_w;

c)   verificare se il coefficiente di correlazione comune r_w è significativamente maggiore di  zero;

d)   verificare se r_w si discosta significativamente dal valore r₀ = 0,32 indicato come valore reale in una pubblicazione presa a riferimento.

 

Risposte.

A)   Dopo aver trasformato i valori di r_i nei corrispondenti valori z_i

 

 

 

 

 ottenendo: z₁ = 0,523;    z₂ = 0,320;    z₃ = 0,389

 si calcola un valore del c² con  gdl= 2

 applicando

Scindendo per comodità di calcolo

 dove

 e

 

 con i dati dell’esempio

 

 risultano A = 64,149

 e

 B = 61,843

 determinando

 un valore di c²₂ = 2,306.

Poiché il valore critico alla probabilità  a = 0.05 con df = 2 è uguale a 5,991 non si può rifiutare l’ipotesi nulla. Una lettura più attenta della tabella dei valori critici evidenzia che il valore calcolato (2,306) è inferiore anche a quello riportato per la probabilità  a = 0.25 che risulta uguale a 2,773.

Si può quindi concludere che i tre coefficienti di correlazione r₁, r₂ e r₃ sono statisticamente uguali.

 

B)   Con questi risultati dell’analisi sulla significatività della differenza tra i k valori campionari, è utile calcolare il coefficiente di correlazione comune r_w, come stima migliore del valore r della popolazione.

Con z₁ = 0,523;    z₂ = 0,320;    z₃ = 0,389   e   n₁ = 120,    n₂ = 100,    n₃ = 150

 il valore di z_w comune

 risulta uguale a 0,414.

Ritrasformato in r_w

 risulta uguale a 0,392.

 

C)   Per la verifica dell’ipotesi nulla H₀: r = 0

 con ipotesi alternativa unilaterale H₁: r > 0

  si utilizzano le varie osservazioni campionarie, per cui

 da r₁ = 0,48;    r₂ = 0,31;    r₃ = 0,37   e   n₁ = 120,    n₂ = 100,    n₃ = 150

 si ottiene

 

 un valore di Z uguale a 7,49.

Poiché nella distribuzione normale unilaterale il valore ottenuto è così grande da non essere nemmeno riportato nella tabella, ad esso è associata una probabilità a estremamente piccola. Di conseguenza, si può concludere che il valore medio r_w è significativamente maggiore di zero.

 

D)   Per la verifica dell’ipotesi nulla H₀: r = r₀

 con ipotesi alternativa bilaterale H₁: r ¹ r₀

 cioè che r_w = 0,392 sia significativamente differente da r₀ = 0,32

 attraverso

 

 dopo aver calcolato il coefficiente di correlazione comune in scala z, cioè z_w = 0,414

 si trasforma nella stessa scala il valore  r₀ = 0,32

 ottenendo

Infine si calcola Z

 ottenendo un valore uguale a 1,58.

In una distribuzione normale bilaterale, a Z = 1,58 corrisponde una probabilità a = 0,114. Non è possibile rifiutare l’ipotesi nulla: r_w = 0,392 non è significativamente differente da  r₀ = 0,32.

 

Correzioni per il bias della trasformazione di Fisher

La trasformazione di r in z con la formula di Fisher determina un errore piccolo, ma sistematico e in eccesso, nel valore di z. E’ un risultato noto da tempo,

-   già evidenziato da H. Hotelling nel 1953 (vedi articolo: New light on the correlation coefficient and its trasformation. Journal Royal Statistical Society B 15, pp. 193-232)

-   e discusso dallo stesso R. A. Fisher nel 1958 (vedi testo: Statistical Methods for Research Workers, 13^th ed., Hafner , New York, 146 pp.).

Ne deriva, in particolare quando si ricorre a test per la significatività della differenza tra k campioni, utilizzando ad esempio la formula già presentata

 

 

  che gli errori si sommano e la differenza tra valore calcolato e valore reale non è più trascurabile. L’errore è tanto maggiore quanto più alto è k.

Per la correzione del bias nel valore di z, ottenuto con la trasformazione di r, le proposte sono numerose. Tra le più frequenti per aggiustare z possono esserne citate due:

 

A)   La formula di Hotelling che, nell’articolo già citato del 1953,

 propone di sottrarre c

al valore z stimato.

Ad esempio, con r = 0,48 calcolato su n = 120

 

 

 si ottiene un valore di z = 0,523

Il valore corretto, ottenuto con la sottrazione della correzione

 

 

  c = 0,004 diventa z’ = z – c = 0,523 – 0,004 = 0,519.

 

B)   La formula di Fisher, proposta nel testo del 1955 per la correzione,

 è

Con lo stesso esempio, la correzione è

 

 c = 0,002  e il valore corretto diventa  z’ = z – c = 0,523 – 0,002 = 0,521.

 

Per il calcolo della significatività della differenza tra più coefficienti, invece di correggere ogni valore z_i e usare la formula generale già presentata, è possibile utilizzare direttamente

 la formula corretta di Paul,

 

 che, come la precedente, utilizza la distribuzione c² con df = k-1.

Ad esempio, applicata agli stessi dati della formula generale che ha stimato un valore di c²₂ = 2,306, con

   r₁ = 0,48;    r₂ = 0,31;    r₃ = 0,37   e   n₁ = 120,    n₂ = 100,    n₃ = 150   e   r_w = 0,392

 si ottiene

 

 

un valore pari a 2,374.

Sempre S. R. Paul nella sua ampia presentazione del 1988 (Estimation of and testing significance for a common correlation coefficient, pubblicato su Communic. Statist. - Theor. Meth. Vol. 17, pp. 39-53) suggerisce che quando r è minore di 0,5 (indicazione approssimata)

-   per il calcolo del coefficiente medio z_w

 al posto di

 sia usato

 

-  e nell’inferenza con ipotesi nulla H₀: r = r₀ per calcolare Z

 al posto di

 sia usata