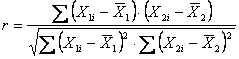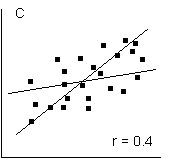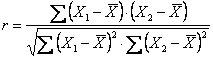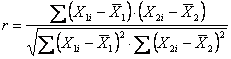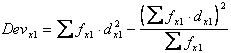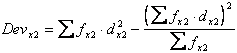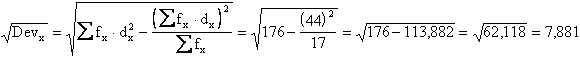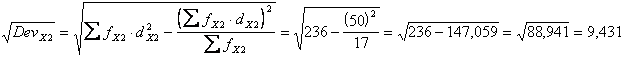CORRELAZIONE  E  COVARIANZA

 

 

18.1.   La correlazione

 

 

La regressione lineare è finalizzata all'analisi della dipendenza tra due variabili, delle quali

-  una (Y) è a priori definita come dipendente o effetto,

-  l'altra (X) è individuata come indipendente o causa.

L'interesse della ricerca è rivolta essenzialmente all'analisi delle cause o allo studio predittivo delle quantità medie di Y, che si ottengono come risposta al variare di X.

Spesso anche nella ricerca ambientale, biologica e medica, la relazione di causa-effetto non ha una direzione logica o precisa: potrebbe essere ugualmente applicata nei due sensi, da una variabile all'altra. Le coppie di fidanzati o sposi di solito hanno altezza simile: la relazione di causa effetto può essere applicata sia dall'uomo alla donna che viceversa; coppie di gemelli hanno strutture fisiche simili e quella di uno può essere stimata sulla base dell'altro.

Altre volte, la causa può essere individuata in un terzo fattore, che agisce simultaneamente sui primi due, in modo diretto oppure indiretto, determinando i valori di entrambi e le loro variazioni, come la quantità di polveri sospese nell’aria e la concentrazione di benzene, entrambi dipendenti dall’intensità del traffico. In altre ancora, l’interesse può essere limitato a misurare come due serie di dati variano congiuntamente, per poi andare alla ricerca delle eventuali cause, se la risposta fosse statisticamente significativa.

In tutti questi casi, è corretto utilizzare la correlazione.

Più estesamente, è chiamato coefficiente di correlazione prodotto-momento di Pearson (Pearson product-moment correlation coefficient), perché nella sua espressione algebrica è stato presentato per la prima volta da Karl Pearson (1857-1936) in un lavoro del 1895. In modo più semplice, anche nel testo di Fisher è chiamato coefficiente di correlazione oppure correlazione del prodotto dei momenti. Il termine correlazione era già presente nella ricerca statistica del secolo scorso, anche se Galton (1822-1911) parlava di co-relation. Sir Galton è stato il primo ad usare il simbolo r (chiamato reversion), ma per indicare il coefficiente angolare b nei suoi studi sull’ereditarietà. La pratica di indicare il coefficiente di correlazione con r diventa generale a partire dal 1920.

La scuola francese sovente utilizza la dizione “coefficiente di correlazione di Bravais-Pearson”, per ricordare il connazionale Bravais (1846), che aveva presentato alcuni concetti importanti di tale metodo cinquanta anni prima di Karl Pearson.

 

Per spiegare le differenze logiche nell’uso della regressione e della correlazione, vari testi di statistica ricorrono a esempi divertenti o paradossali. Uno di questi è quanto evidenziato da un ricercatore dei paesi nordici. In un’ampia area rurale, per ogni comune durante il periodo invernale è stato contato il numero di cicogne  e quello dei bambini nati. E’ dimostrato che all’aumentare del primo cresce anche il secondo.

Ricorrere all'analisi della regressione su queste due variabili, indicando per ogni comune con X il numero di cicogne e con Y il numero di nati, implica una relazione di causa-effetto tra presenza di cicogne (X) e nascite di bambini (Y). Anche involontariamente si afferma che i bambini sono portati dalle cicogne; addirittura, stimando b, si arriva ad indicare quanti bambini sono portati mediamente da ogni cicogna.

In realtà durante i mesi invernali, nelle case in cui è presente un neonato, la temperatura viene mantenuta più alta della norma, passando indicativamente dai 16 ai 20 gradi centigradi. Soprattutto nei periodi più rigidi, le cicogne sono attratte dal maggior calore emesso dai camini e  nidificano più facilmente su di essi o vi si soffermano più a lungo. Con la correlazione si afferma solamente che le due variabili cambiano in modo congiunto.

L'analisi della correlazione misura solo il grado di associazione spaziale o temporale dei due fenomeni; ma lascia liberi nella scelta della motivazione logica, nel rapporto logico tra i due fenomeni. Il coefficiente r è una misura dell’intensità dell’associazione tra le due variabili.

 

Una presentazione chiara dell’uso della correlazione è fornita da Fisher stesso. Nonostante l’italiano del traduttore risenta del periodo, sulla base di una cultura biologica minima è possibile comprendere il ragionamento e la procedura che dovrebbero anche oggi caratterizzare il biologo. Si riafferma il concetto di non attribuire troppa importanza al puro aspetto statistico, se sganciato dal problema; è necessario utilizzare le due competenze congiuntamente. Nel caso particolare, un aspetto culturale importante è la presentazione dell’ereditarietà nell’uomo, tipica della cultura di Fisher, della sua scuola e del periodo storico a partire da Galton. In “Metodi statistici ad uso dei ricercatori, Torino 1948, Unione Tipografica Editrice Torinese (UTET), 326 p. traduzione di M Giorda, del testo Statistical Methods for Research Workers di R. A. Fisher 1945, nona edizione (la prima nel 1925) a pag. 163 si legge:

Nessuna quantità è più caratteristicamente impiegata in biometrica quanto il coefficiente di correlazione e nessun metodo è stato applicato a tanta varietà di dati quanto il metodo di correlazione. Specialmente nei casi in cui si può stabilire la presenza di varie cause possibili contribuenti a un fenomeno, ma non si può controllarle, i dati ricavati dall’osservazione hanno con questo mezzo assunto un’importanza assolutamente nuova. In un lavoro propriamente sperimentale, peraltro, la posizione del coefficiente di correlazione è molto meno centrale; esso, infatti, può risultare utile negli stadi iniziali d’una indagine, come quando due fattori che sono ritenuti indipendenti, risultano invece associati; ma è raro che, disponendo di condizioni sperimentali controllate, si intenda esprimere una conclusione nella forma di un coefficiente di correlazione.

Uno dei primi e più notevoli successi del metodo della correlazione si riscontrò nello studio biometrico dell’ereditarietà. In un tempo in cui nulla si conosceva del meccanismo dell’ereditarietà o della struttura della materia germinale, fu possibile, con questo metodo, dimostrare l’esistenza dell’ereditarietà e “misurarne l’intensità”; questo in un organismo nel quale non si potrebbero praticare allevamenti sperimentali, cioè nell’Uomo. Comparando i risultati ottenuti dalle misurazioni fisiche sull’uomo, con quelli ottenuti su altri organismi, si stabilì che la natura dell’uomo è governata dall’ereditarietà non meno di quella del resto del mondo animato. Lo scopo dell’analogia fu ulteriormente allargato dalla dimostrazione che coefficienti di correlazione della stessa grandezza si potevano ottenere tanto per le misurazioni fisiche, quanto per le qualità morali ed intellettuali dell’uomo.

Questi risultati rimangono di importanza fondamentale perché, non soltanto l’ereditarietà nell’uomo non è ancora suscettibile di studi sperimentali e gli attuali metodi di prova riguardanti l’intelletto sono, tuttora, inadatti ad analizzare le disposizioni intellettuali, ma perché, anche con organismi passibili di esperimenti e di misurazioni, è soltanto nel più favorevole dei casi che coll’ausilio dei metodi mendeliani possono essere determinati i diversi fattori causanti la variabilità incostante e studiati i loro effetti. Tale variabilità fluttuante, con una distribuzione pressoché normale, è caratteristica della maggioranza delle varietà più utili delle piante e degli animali domestici; e, quantunque, ci sia qui una forte ragione per ritenere che in tali casi l’ereditarietà è, in definitiva, mendeliana, il metodo biometrico di studio è, oggi giorno, il solo capace di alimentare le speranze di un reale progresso.

Questo metodo, che è anticamente basato sul coefficiente di correlazione, conferisce a questa quantità statistica un’effettiva importanza anche per coloro che preferiscono sviluppare la loro analisi con altri termini.

 

Nella correlazione, le due variabili vengono indicate con X₁ e X₂, non più con X (causa) e Y (effetto), per rendere evidente l'assenza del concetto di dipendenza funzionale. (Purtroppo, in vari lavori sono usati ugualmente X e Y, senza voler implicare il concetto della regressione).

 

L'indice statistico (+r   oppure   –r) misura

-  il tipo (con il segno  + o -)

-  e il grado (con il valore assoluto)

di interdipendenza tra due variabili.

 

Il segno indica il tipo di associazione:

-  positivo, quando le due variabili aumentano o diminuiscono insieme,

-  negativo, quando all'aumento dell'una corrisponde una diminuzione dell'altra o viceversa.

Il valore assoluto varia da 0 a 1:

-  è massimo (uguale a 1) quando c'è una perfetta corrispondenza lineare tra X₁ e X₂;

-  tende a ridursi al diminuire della corrispondenza ed è zero quando essa è nulla.

 

L’indicatore della correlazione r è fondato sulla Codevianza e la Covarianza delle due variabili.

La Codevianza e la Covarianza tra X₁ e X₂ (Cod_X1/X2  e  Cov_X1/X2) hanno la proprietà vantaggiosa di contenere queste due informazioni sul tipo (segno) ed sul grado (valore) di associazione; ma presentano anche lo svantaggio della regressione, poiché il loro valore risente in modo determinante della scala con la quale le due variabili X₁ e X₂ sono misurate.

Quantificando il peso in chilogrammi oppure in grammi e l'altezza in metri oppure in centimetri, si ottengono valori assoluti di Codevianza con dimensioni diverse, appunto perché fondati sugli scarti dalle medie ():

Cod_X1/X2 =

 

E’ possibile pervenire a valori direttamente comparabili, qualunque sia la dimensione dei due fenomeni, cioè ottenere valori adimensionali, solo ricorrendo ad unità standard, quale appunto la variazione tra – 1 e +1 . Si perviene ad essa,

-  mediante il rapporto tra la codevianza e la media geometrica delle devianze di  X₁ e X₂:

 

 

In realtà la definizione è basata sulla covarianza e le due varianze: la stima della correlazione è il rapporto tra la covarianza e la media geometrica delle due varianze. Tuttavia, dato che le varianze sono ottenute dividendo le devianze per n (oppure i gradi di libertà in caso di campioni come sempre usato nelle formule presentate), anche nel testo di Fisher si afferma che conviene basare il calcolo sulla codevianza e devianze

 

Per comprendere il significato geometrico dell’indice r di correlazione e derivarne la formula, un approccio semplice è il confronto tra le due rette di regressione, calcolate dai valori di X₁ e X₂:

-   la prima calcolata con X₁ usata come variabile dipendente e X₂ come variabile indipendente;

-   la seconda scambiando le variabili, quindi utilizzando X₂ come dipendente e X₁ come indipendente. (Per meglio distinguere le due rette, anche se errato è qui conveniente utilizzare X e Y per le due variabili)

 

 

 

 

 

 

 

 

 

 

 

 

 

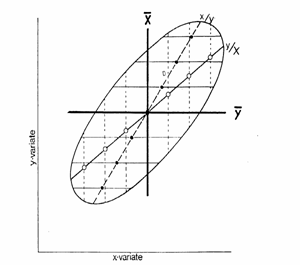
Nella figura precedente, l'ellisse (la superficie contenuta nella figura piana chiusa) descrive la distribuzione di una nuvola di punti.

Quando si calcola la retta di regressione classica, presentata nel capitolo relativo,

Y = a + bX

 si ottiene la retta indicata con i punti vuoti (o bianchi).

Se si scambiano le variabili e si stima

X = a+bY

 si ottiene la retta indicata dai punti in nero.

Entrambe passano da baricentro della distribuzione, individuato dall'incontro delle due medie ( e ), ma ognuna di esse è più vicina, in modo simmetrico, alla media della variabile indicata come effetto (la prima a Y e la seconda a X).

Il valore di correlazione lineare r  può essere ricavato dai due coefficienti angolari b.

Le due rette coincidono solamente quando i punti sono disposti esattamente lungo una retta.

 

 

 

 

Le due rette, riportate in ognuna dei 6 figure precedenti, sono calcolate sulle stesse coppie di osservazioni, scambiando appunto X₁ e X₂. Esse

-   i intersecano nel baricentro della distribuzione, il punto che rappresenta il valore medio di X₁ e di X₂;

-   ma non sono identiche o coincidenti (eccetto nella figura A, in cui r = 1), poiché entrambe tendono ad avvicinarsi alla media della variabile assunta come dipendente.

Quando le due rette sono tra loro perpendicolari (figura D e figura E) con angoli di 90° e coincidono con le due medie, le due variabili sono indipendenti e tra loro non esiste alcuna correlazione (r = 0); inversamente, quando le due rette tendono ad avvicinarsi con un angolo minore, il valore assoluto della correlazione tende ad aumentare (figura C e figura B). Il valore massimo (r = 1) viene raggiunto quando le due rette coincidono e l’angolo tra esse è nullo (figura A).

 

Il segno della correlazione dipende dal coefficiente angolare delle due rette: è positivo, se il loro coefficiente angolare è positivo, mentre è negativo quando il coefficiente angolare è negativo. Pertanto il valore di r può variare tra +1 e -1.

(Tra le figure non sono stati riportati valori di r negativi: la distribuzione dei punti avrebbe evidenziato una diminuzione dei valori della ordinata al crescere di quelli in ascissa e quindi le due rette avrebbero avuto una inclinazione verso il basso all’aumentare dell’ascissa.)

 

E' importante ricordare che un valore assoluto basso o nullo di correlazione non deve essere interpretato come assenza di una qualsiasi forma di relazione tra le due variabili:

-  è assente solo una relazione di tipo lineare,

-  ma tra esse possono esistere relazioni di tipo non lineare, espresse da curve di ordine superiore, tra le quali la più semplice e frequente è quella di secondo grado.

 

L'informazione contenuta in r riguarda solamente la quota espressa da una relazione lineare.

 

Per derivare la formula di r da quanto già evidenziato sulla regressione lineare semplice, è utile ricordare che essa può essere vista come la media geometrica dei due coefficienti angolari (b) di regressione lineare.

 

Infatti, indicando con

-  b_{x1 / x2}  il coefficiente angolare della prima retta di regressione,

-  b_{x2 / x1}  il coefficiente angolare della seconda retta di regressione,

 il coefficiente di correlazione r può essere stimato

 come

 

Poiché

b_{(i / j )} =

 

 e dato che le due Codevianze sono identiche,

 

dopo semplificazione,

nella formulazione estesa con la consueta simbologia

si ottiene

 

 

Per calcolare il coefficiente di correlazione da una serie di rilevazioni, si possono presentare due casi distinti:

-  il primo, con poche osservazioni, quando i dati sono forniti come coppie distinte di valori;

-  il secondo, con molte osservazioni, quando i dati sono stati raggruppati in classi di frequenza.

 

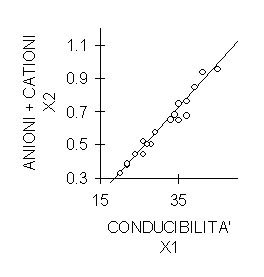
La formula sopra riportata è applicabile nel caso di osservazioni singole.

ESEMPIO.  In 18 laghi dell'Appennino Tosco-Emiliano sono state misurate la conducibilità e la concentrazione di anioni + cationi, ottenendo le coppie di valori riportati nella tabella

 

 

 

Calcolare il coefficiente di correlazione tra queste due variabili 

a)  -  in modo diretto e

b)  -  mediante i due coefficienti angolari,

 per meglio comprendere l’equivalenza delle due formule.

 

Risposta.

A)  In modo diretto, con la formula che utilizza le singole coppie di valori

 

si ottiene un valore di r

 

r =  = 0,987

uguale a 0,987.

Utilizzando i coefficienti angolari delle due regressioni, che dai calcoli risultano

 

 

e che sono rappresentati nelle due figure seguenti

 

 

 il coefficiente di correlazione

 

 

 risulta uguale a 0,9876

 con una differenza, dalla stima precedente, determinata dagli arrotondamenti.

 

Nel caso di osservazioni raggruppate in classi, il metodo per calcolare l'indice di correlazione resta sostanzialmente invariato, rispetto a quello presentato nel capitolo sulla statistica descrittiva.

Per ogni classe, come valore rappresentativo viene assunto il valore centrale; le differenze tra questi valori centrali di ogni classe ed il valore centrale di tutta la distribuzione devono essere moltiplicate per il numero di osservazioni.

 

Per semplificare i calcoli e per una esatta comprensione del fatto che le variazioni di scala non incidono assolutamente sul valore di r (che è adimensionale) è possibile utilizzare non i valori osservati ma gli scarti delle grandezze da una qualsiasi origine arbitraria. Di norma è quella centrale, in quanto determina scarti minimi e simmetrici.

La classe di frequenza centrale o prossima al centro viene indicata con zero e le altre con il numero progressivo, positivo a destra e negativo a sinistra, di distanze unitarie da essa.

 

Per esempio, la distribuzione di X₁ in 7 classi

 

 

 

che potrebbe utilizzare i valori centrali relativi (60, 80, 100, 120, 140, 160, 180) per il calcolo dell’indice r di correlazione può essere utilmente trasformata in una scala unitaria

 

 

 

mentre la distribuzione della variabile X₂ in 6 classi

 

 

può essere trasformata in

 

 

un’altra distribuzione arbitraria equivalente, seppure non simmetrica come la precedente.

E’ intuitivo che, con questi nuovi dati, i prodotti e le somme necessarie alla stima del coefficiente di correlazione r risultano molto semplificati, per un calcolo manuale. Sono quindi tecniche del passato, superate dalle nuove possibilità offerte dall’informatica, con la quale non si pongono problemi di semplificazione dei calcoli. Restano però importanti i concetti: l’indice di correlazione r tra due variabili è adimensionale, fornisce lo stesso valore al variare delle scale di misura.

 

Ritornando al concetto dell’invarianza del valore di r rispetto al tipo di scala, nulla muterebbe nel suo valore se la prima o la seconda distribuzione fossero trasformate in una scala ancora differente, come la seguente

 

 

 

Con dati raggruppati in distribuzioni di frequenze, il coefficiente di correlazione r può essere ottenuto con la solita formula

 

 in cui la Codevianza di X₁ e X₂ è data da

 

 

 e le due devianze da

 la prima

 e da

 la seconda,

 dove

-  d_X1  e  d_X2   sono gli scarti, misurati su una scala arbitraria, dei valori delle classi dall'origine scelta;

-  f_X1  e  f_X2   sono le frequenze dei valori di X₁ e di X₂ entro ciascuna classe;

-  f_X1X2          sono le frequenze delle coppie X₁-X₂ entro ciascuna coppia di classi.

 

 

ESEMPIO 1.   Da una serie di rilevazioni effettuate su un campione d’acqua di 17 laghi (riportate nella tabella successiva)

A -  costruire la relativa tabella a doppia entrata di distribuzione delle frequenze e

B -  calcolare da essa il coefficiente di correlazione semplice r.

 

 

Risposte

A)  Dai dati,  è possibile ricavare la tabella a doppia entrata, come quella di seguito riportata

 

 

 

Nel riquadro interno della tabella sono riportate le f_x1x2 e (tra parentesi) i prodotti fx×d_x1×d_x2 che saranno utilizzati per il calcolo della codevianza. Non sono state riportate le frequenze nulle.

I vari passaggi necessari per stimare la Devianza di X₁ dai dati della distribuzione in classi sono riportati nella tabella successiva

 

 

 

 

Con la formula abbreviata

 

 

 si ottiene la radice quadrata della devianza di X₁, utile ai calcoli successivi, che è uguale a 7,88.

 

Seguendo le stesse modalità, il calcolo della Devianza di X₂ e della sua radice quadrata (i cui passaggi sono riportati nella tabella successiva)

 

 

 fornisce un risultato di 9,43.

 

Dalle due tabelle è possibile ottenere i dati necessari alla stima della Codevianza

 

 

 dove  

 che risulta uguale a 71,588

 

Il coefficiente di correlazione r

 

 risulta uguale a 0,963.

E’ semplice verificare empiricamente, come dimostrano i calcoli successivi, che anche cambiando i valori di d_X1 e d_X2 il coefficiente di correlazione non cambia.

 

 

 

Si può infatti notare le f_X1 ed f_X2 sono rimaste inalterate, mentre sono cambiate le f_X1X2

La radice quadrata della Devianza di  X₁

i cui passaggi sono riportati nella tabella successiva

 

 

 

 

risulta uguale a 7,881

e la radice quadrata della devianza di X₂

 

 

 

 risulta uguale a 9,431.

 

La Codevianza di X₁ e X₂

 

 

 dove

 

= 201 -  = 201 - 129,412 = 71,588

 risulta uguale a 71,588.

Essendo rimaste invariate sia la Codevianza che le Devianze, il coefficiente di correlazione semplice r non può che rimanere identico.