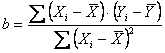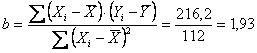LA REGRESSIONE LINEARE SEMPLICE

 

 

16.5.   LA REGRESSIONE LINEARE SEMPLICE

 

 

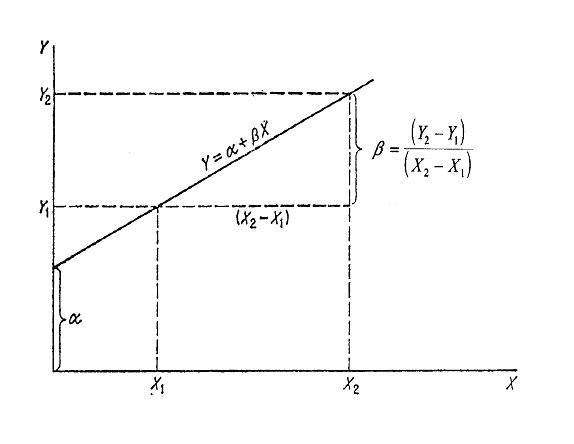
La relazione matematica più semplice tra due variabili (con X variabile indipendente e Y variabile dipendente) è la regressione lineare semplice, rappresentata dall’equazione

 dove

- _i  è il valore stimato o predetto per il valore  dell'osservazione ,

-   è il valore empirico o campionario di  della stessa osservazione ,

-   è l'intercetta della retta di regressione,

-   è il coefficiente angolare: indica la quantità unitaria di cui cambia  al variare di una unità di .

I due parametri  e  sono tra loro indipendenti

 

La rappresentazione grafica evidenzia che

 

 

- il termine , chiamato intercetta e indicato con  quando riferito alla popolazione, fissa la posizione della retta rispetto all’asse delle ordinate:   è il valore di Y, quando X è uguale a 0.

 

-  il termine , chiamato coefficiente angolare e indicato con  quando riferito alla popolazione, indica l’aumento di Y all’aumento di Y tra due punti di coordinate   e 

 

 

Due rette che differiscano solo per il valore di , quindi con  uguale, sono tra loro parallele.

 

Un generico punto  sul diagramma è individuato

 dall’equazione

 

 

 

Come evidenziato nella figura,

- ogni punto sperimentale  ha una componente di errore ,

 che graficamente è rappresentato da

-  lo scarto verticale del valore campionario dalla retta;

 quindi, dalla distanza tra la  osservata e la  collocata sulla retta.

Poiché la retta di regressione serve per predire Y sulla base di X,

- l’errore  commesso è quanto la Y predetta () dista dalla Y osservata ().

 

Per costruire la retta che descrive la distribuzione dei punti, il principio al quali riferirsi può essere differenti. Da essi derivano metodi diversi.

Gli statistici hanno scelto il metodo dei minimi quadrati (least squares) chiamata anche, dai biologi, regressione Model I.

In un capitolo successivo, è discussa la retta di regressione dei minimi prodotti  (least products) chiamata anche, regressione Model II.

La retta least-squares è quella che

- riduce al minimo la somma dei quadrati degli scarti di ogni punto dalla sua proiezione verticale (parallelo all’asse delle Y).

 

In modo più formale, indicando con

 -   il valore osservato od empirico e con

 -  _i il corrispondente valore sulla retta,

 si stima come migliore interpolante quella che è maggiormente in accordo

 con la condizione

= minimo

Poiché

 è possibile scrivere

 

 

Calcolando la derivata di  rispetto a   e   e ponendo uguale a 0 la seguente coppia di equazioni (chiamata equazione normale)

 

 e

 si trova

 e

 che è più facile ricordare con la dizione

 

La codevianza è un concetto non ancora incontrato nel corso di statistica, poiché serve nello studio di due variabili: stima come X e Y variano congiuntamente, rispetto al loro valore medio.

E' definita come

-  la sommatoria degli n  prodotti degli scarti di X rispetto alla sua media e di Y rispetto alla sua  media:

 

Come la devianza, anche la codevianza ha una formula empirica od abbreviata che permette un calcolo più rapido

 

 e preciso a partire dai dati campionari.

Infatti evita l’uso delle medie, che sono quasi sempre valori approssimati e impongono di trascinare nei vari calcoli alcuni decimali.

 

 

Dopo aver calcolato , si stima :

 

Il concetto di codevianza è di grande importanza, in quanto sta alla base sia della statistica bivariata, qui discussa, che della statistica multivariata.

Il punto di incontro delle due medie  e , che è sempre utile tracciare in un diagramma di dispersione, identica il baricentro della distribuzione dei punti.

 

 

 

Per costruzione del valore dell’intercetta  

 e del coefficiente angolare  

 

- la retta di regressione passa sempre attraverso questo punto.

 

Le due medie  e  dividono lo spazio cartesiano in 4 quadranti. La distribuzione dei punti in essi, determina se il valore del coefficiente angolare  sarà (I) positivo, (II) nullo oppure (III) negativo.

 

1 - Quando un punto  è collocato in alto a destra (primo quadrante),

-  il valore di  è maggiore della sua media  e quindi la quantità  è positiva

-  il valore di  è maggiore della sua media  e quindi la quantità   è  positiva

 e quindi la codevianza

 risulta positiva.

 

2 - Quando un punto  è collocato in basso a sinistra (terzo quadrante),

 - entrambi gli scarti sono positivi e quindi la codevianza è positiva.

 

3  e 4 - Quando un punto  è collocato in basso a destra (secondo quadrante)

 oppure in alto a sinistra (quarto quadrante)

- uno scarto è positivo e l’altro è negativo e quindi la codevianza è negativa.

 

Considerando globalmente una serie di  punti collocati in tutti i quattro quadranti del diagramma di dispersione,

-  la Codevianza  

 

-  e quindi il coefficiente angolare  

 

a) sono positivi quando i punti sono collocati prevalentemente nei quadranti 3 e 1,

b) sono negativi quando i punti sono collocati prevalentemente nei quadranti 4 e 2,

c) sono prossimi a 0 e possono al limite diventare nulli, quando i punti sono distribuiti in modo equilibrato nei 4 quadranti.

 

Calcolati i valori dell'intercetta  e del coefficiente angolare , è possibile procedere alla rappresentazione grafica della retta.

Anche a questo scopo, è importante ricordare che la retta passa sempre dal baricentro del diagramma di dispersione, individuato dal punto d'incontro delle due medie   e .

Di conseguenza, è sufficiente

- calcolare il valore di  corrispondente ad un solo qualsiasi valore di  

(ovviamente diverso dalla media), per tracciare con una riga

- la retta che passa per questo punto calcolato (, ) e per il punto d'incontro delle due medie  (, ).

 

Quando i calcoli sono stati effettuati manualmente, è possibile commettere un errore qualsiasi, per cui la retta calcolata

 è errata in almeno uno dei due parametri.

Se non sono stati commessi errori di calcolo, qualsiasi altro punto  stimato per un valore  differente dal precedente nella rappresentazione grafica deve risultare collocato esattamente sulla retta tracciata.

E’ un concetto elementare, che può servire come procedimento semplice ed empirico, per verificare la correttezza di tutti i calcoli effettuati fino a quel punto.

 

 

ESEMPIO 1.  (DATI BIOLOGICI: RELAZIONE TRA ALTEZZA E PESO, IN DONNE)

Per sette studentesse universitarie, indicate con lettere, è stato misurato il peso in Kg e l'altezza in cm.

 

 

 

 

Calcolare la retta di regressione che evidenzi la relazione tra peso ed altezza.

 

Risposta.   Come primo problema è necessario individuare quale è la variabile indipendente, che deve essere indicata con X, e quale la variabile dipendente, indicata con Y. Se non esiste tale relazione unidirezionale di causa - effetto, da motivare con conoscenze della disciplina che esulano dalla statistica, è più corretto utilizzare la correlazione lineare semplice.

Tra le due serie di misure dell’esempio, la variabile indipendente è l'altezza e la variabile dipendente è il peso. Infatti ha significato stimare quanto dovrebbe pesare un individuo in rapporto alla sua altezza, ma non viceversa.

 

Successivamente, dalle 7 coppie di dati si devono calcolare le quantità

 

 

 che sono necessarie per

-   la stima del coefficiente angolare

 

 

 che risulta uguale a 0,796

 

-   la stima dell’intercetta

che risulta uguale a -73,354.

 

Si è ricavata la retta di regressione

_i = -73,354 + 0,796 × X_i

 con la quale è possibile stimare i punti sulla retta, corrispondenti a quelli sperimentalmente rilevati.

 

Per tracciare la retta

- è sufficiente calcolare un solo altro punto,

 oltre a quello già noto, individuato dall’incrocio delle due medie, che identifica il baricentro della distribuzione.

Di norma, ma non necessariamente per questo scopo, l’ulteriore punto che serve per tracciare la retta è calcolato entro il campo di variazione delle X_i empiriche.

Successivamente, si deve prolungare il segmento che per estremi ha il punto stimato ed il baricentro della distribuzione, come nella figura di seguito riportata.

 

 

Qualsiasi altro valore di _i , stimato a partire da un generico X_i , sarà collocato su questa retta, se non sono stati commessi errori di calcolo.

 

Anche nella regressione, è necessario non fermarsi ai calcoli statistici, ma interpretare i valori del coefficiente angolare   e dell’intercetta .

Nel sua interpretazione biologica, il valore calcolato di  

- indica che in media gli individui che formano il campione aumentano di 0,796 Kg. al crescere di 1 cm. in altezza.

Visivamente si evidenzia anche che, rispetto alla media del campione e in rapporto all’altezzza,

- la studentessa più grassa è la E, con altezza cm. 166 e peso Kg 63;

- la studentessa più grassa è la F, con altezza cm. 175 e peso Kg 59.

 

E’ quindi ovvio che, se l’altezza delle 7 studentesse fosse stata misurata in metri (1,60; 1,78; ...), il coefficiente angolare  sarebbe risultato uguale a 79,6 (cento volte il valore precedente uguale a 0,796), indicando l’incremento medio di 79,6 kg. per l’aumento di 1 metro in altezza.

Nello stesso modo e simmetricamente, se il peso fosse stato stimato in ettogrammi (520, 680, ...) e l’altezza sempre in centimetri, il coefficiente angolare  sarebbe risultato uguale a 7,96 indicando un aumento medio del peso di hg. 7,96 per un aumento di 1 cm in altezza.

Sono concetti da tenere sempre presenti, quando si devono confrontare due o più coefficienti angolari calcolati con misure differenti.

 

Il valore di  sovente non è importante.

Spesso serve solamente per calcolare i valori sulla retta: ha uno scopo strumentale e nessun significato biologico.

In questo esempio, nella realtà  non esiste. Infatti è fuori dal campo di variazione logica della X; con un concetto più esplicito, non esiste alcuna persona con l’altezza 0 (zero).

L’intercetta  ha significato solo in pochi casi. Ad esempio, quando si confrontano due metodi per stimare la stessa quantità, che potrebbe essere nulla.

Se per X = 0 si ha che l’intercetta è  si deve concludere che Y  0. Quando si confrontano due metodi di misurazione, come possono essere due bilance,  significa che i due strumenti hanno una taratura differente, per una quantità che è indicata dal valore di . In questi casi, sarà logico verificare se tale valore è statisticamente diverso da 0 oppure se ne può rappresentare una variazione campionaria.

Sono concetti che saranno ripresi nel paragrafo dedicato alla significatività di  e alla stima del suo intervallo di confidenza.

 

ESEMPIO 2. (DATI CHIMICI: RELAZIONE TRA CONCENTRAZIONE E FLUORESCENZA)

Nelle analisi chimiche è frequente l’uso di strumenti che emettono un segnale, come risposta alla concentrazione di un analita. La funzione della risposta può essere lineare, logaritmica, esponenziale oppure ogni altra funzione; inoltre, può variare a concentrazioni differenti.

In questo caso, sono state preparate 7 concentrazioni (pg/ml) differenti ed è stata misurata l’intensità della loro fluorescenza.

 

 

 

1) Costruire il diagramma di dispersione.

2) Calcolare la retta di regressione e riportarla nel grafico.

Risposta. La prima elaborazione dei dati è il calcolo delle due medie, della codevianza e della devianza della X, come nella tabella successiva:

 

 

 

Le coppie di valori (, ) permettono di costruire il diagramma cartesiano con i 7 punti.

Le due medie  = 6  e   = 13,1 consentono di tracciare le due rette e di individuare il baricentro della distribuzione dei punti.

 

 

Dalla Devianza    = 112   e dalla Codevianza   = 216,2

 si ricava il coefficiente angolare

 

 

Da esso e dalle due medie   = 6  e   = 13,1

 si ricava l’intercetta

 

Ne consegue che la retta di regressione lineare semplice

 è

 

Per tracciare la retta, che ovviamente passa per due punti,

- il primo è noto essendo il baricentro, già identificato;

- il secondo è individuato scegliendo un valore qualsiasi della variabile , come può essere  = 1,

 e ricavando da esso il valore stimato  corrispondente,

 che risulta

 

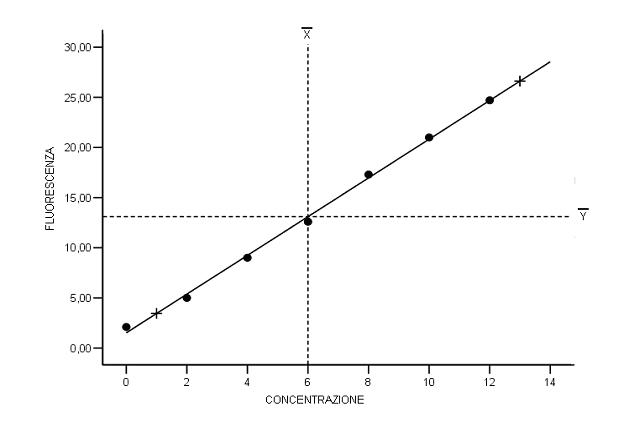
Nel diagramma cartesiano, si identifica il punto di coordinate , .

Esso risulta individuato dalla crocetta in basso a sinistra.

Si traccia la retta unendo i due punti con una riga e proseguendo almeno fino ai due estremi della variabile X.

 

Se, come in questo caso, i calcoli sono stati fatti manualmente, è possibile che sia stato commesso almeno un errore. Una verifica empirica della loro correttezza, quindi delle statistiche della retta (=1,5 e  =1,93) è fondato sulla stima delle coordinate di un altro punto. Se esso viene collocato esattamente sulla retta, tutti i calcoli sono corretti. Se il punto è collocato fuori dalla retta già tracciata, è necessario rivedere i calcoli effettuati poiché contengono senza dubbio almeno un errore.

 

In questo caso, assumiamo di prendere   = 13 (a questo scopo non importa se è maggiore dell’ultima X osservata)

Il valore stimato  corrispondente è

 

Nel diagramma cartesiano identifica il punto di coordinate  e

 che risulta individuato dalla crocetta in alto a destra.

Cade esattamente sulla retta già tracciata (con le approssimazione alla prima cifra decimale, come nei calcoli effettuati). La retta di regressione lineare calcolata è corretta.

 

I due tipi di esempi (il primo con variabili biologiche e il secondo con variabili chimiche) richiedono la stessa metodologia per stimare la retta. Ma evidenziano caratteristiche differenti e la interpretazione disciplinare dei risultati  è differente.

E’ semplice osservare come i punti dell’esempio 2 sono molto più vicini alla retta, rispetto a quelli dell’esempio 1. In variabili chimiche, la dispersione dei punti quasi sempre è nettamente minore di quella che è presente nelle variabili biologiche, agrarie, ecologiche e mediche. In esse, le differenze sia ambientali sia tra individui giocano un fattore molto importante, per cui spesso la significatività della retta non è dimostrata, a causa della distanza dei punti osservati  da quelli predetti , individuati dalla retta.

Anche la predittività, altro concetto che sarà discusso successivamente, è nettamente differente.

Sono aspetti che hanno ricadute molto importanti sulle misure della retta. Pertanto, esse dovranno sempre essere interpretate entro la singola disciplina, nella quale è posto il problema statistico.

Ad esempio, nel caso delle due variabili chimiche l’intercetta  assume un significato nettamente diverso, da quello che aveva con le due variabili biologiche. Rappresenta l’intensità di fluorescenza, presente, quando la concentrazione dell’analita è zero.

 

Da queste osservazioni derivano altri problemi, che saranno discussi successivamente. Tra i più importanti, per quanto riguarda le analisi di laboratorio, ne emergono due.

1) Quale è la concentrazione minima che può essere rilevata, con quel metodo?

 

La retta è stata calcolata determinando

-  l’intensità della fluorescenza (), conoscendo la quantità di concentrazione ().

In realtà, spesso il problema che si deve affrontare è l’opposto:

2) Come posso risalire alla concentrazione (), per un certo valore dell’intensità della fluorescenza (), in un campione?

E’ la regressione inversa o calibrazione, anch’essa discussa nei paragrafi successivi.