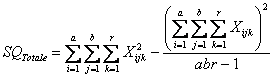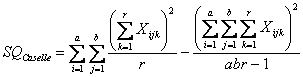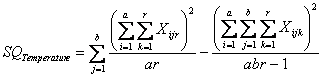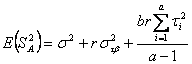L’ANALISI GERARCHICA E

LE COMPONENTI DELLA VARIANZA

 

 

 

14.13.  ESEMPIO DI ANALISI DELLA VARIANZA A DUE FATTORI CON INTERAZIONE, IN UN MODELLO A EFFETTI FISSI E UNO A EFFETTI RANDOM, SU GLI STESSI DATI; ESEMPIO DI STIMA DELLE COMPONENTI DELLA DEVIANZA.

 

 

Il caso più semplice di esperimento fattoriale prende in considerazione solamente due fattori o trattamenti (A e B), ognuno a più livelli, che possono essere indifferentemente uguali o differenti. L’analisi statistica verifica separatamente gli effetti nei diversi livelli

- sia dei due singoli trattamenti (A e B),

- sia della loro interazione (A x B).

 

Agli stessi dati e con metodologie in larga parte identiche, ma per rispondere a domande differenti, è possibile applicare

A - sia l’ANOVA I chiamata anche  modello a effetti fissi (fixed effects model),

B  - sia l’ANOVA II chiamata anche modello a effetti random (random effects model) o modello delle componenti di varianza (components of variance model),

C - sia l’ANOVA III, dove un fattore è fisso e l’altro è random, chiamata modello misto (mixed model); in caso di più fattori, almeno uno è fisso e almeno uno è randon.

 

Per analizzare l’interazione tra due variabili, esse devono sempre essere crossed; in un disegno sperimentale nested o gerarchica, in cui una variabile è annidata entro l’altra, non è possibile.

I concetti generali dell’analisi a effetti fissi e di quella a effetti random sono già stati presentati nei paragrafi precedenti. In questo, viene riportata una loro applicazione agli stessi dati,

- per meglio evidenziare la parte simile e le differenze.

L’esempio sviluppato è tratto dal testo di

-  Douglas C. Montgomery del 1976 Design and Analysis of Experiments (edito da John Wiley & Sons, New York, XIV + 418 p.).

Docente di metodi statistici nel Georgia Institute of Technology, Montgomery è autore di vari testi di statica applicata alla ricerca industriale. In questo volume, che ha ormai 30 anni, espone una serie di applicazioni dell’analisi della varianza. Rispetto al testo, il suo esempio è svolto giustificando tutti i passaggi logici.

 

I concetti della varianza qui discussi stanno alla base di molti metodi statistici industriali, ora utilizzati correntemente per il controllo di qualità. In questi anni, queste applicazioni stanno assumendo importanza crescente anche nelle discipline ambientali e biologiche, quando la gestione dell’ambiente o di un prodotto biologico richiedano confronti sulla variabilità più che sui valori medi.

 

In queste dispense, in particolare per gli aspetti più complessi, molti esercizi sono tratti da testi internazionali. Con la dovuta citazione, offrono la possibilità di supportare la metodologia scelta in pubblicazioni scientifiche e rapporti anche con l’autorevolezza scientifica dell’autore del testo, in eventuali dibattiti con i referee. Tale motivazione a maggior ragione è valida in questo contesto, dove le differenze tra i metodi dipendono quasi esclusivamente dalla scelta del problema, dalla giustificazione fornita per un confronto a effetti fissi oppure a effetti random, dalla una diversa interpretazione degli stessi dati.

 

Nell’esempio utilizzato, si intende confrontare il voltaggio massimo di una serie di batterie, tenendo in considerazione

-  il materiale (fattore A), la temperatura di esercizio (fattore B),

-  e la eventuale presenza di interazione tra essi.

Ognuno dei due fattori è a tre livelli e sono state fatte quattro repliche per ogni condizione sperimentale.

 

In questo caso, come in vari testi e diversamente dalle altre parti di queste dispense,

-  il fattore principale (i trattamenti) è riportato nelle righe,

-  mentre il fattore secondario o da controllare (i blocchi) è riportato nelle colonne:

 

 

 

 

 

A – ANOVA I O MODELLO A EFFETTI FISSI

Nel caso del modello ANOVA a due criteri con repliche, per l’analisi degli effetti fissi, ogni singola osservazione  può essere descritta dal modello statistico lineare

 

 dove

-  = media generale di tutti gli effetti; con i dati del campione è quantificata da ,

-  = effetto vero del livello  -esimo del fattore A; con i dati del campione è stimata con ,

-  = effetto vero del livello  -esimo del fattore B; con i dati del campione è stimata con ,

-  = effetto dell’interazione tra  e ; con i dati del campione per ogni casella è determinato dalla differenza () tra la media osservata  e la media attesa ;

-  = componente dovuta all’errore casuale o random, presente in ogni osservazione.

 

Nell’esempio,  = 3,     = 3,     = 4,   

 

Come in ogni test, è necessario iniziare dall’enunciazione delle finalità.

 

Nel modello a effetti fissi, le ipotesi da verificare possono essere 

1 - per i trattamenti o fattore A

H₀:       scritto anche come      H₀:

2 - per i blocchi o fattore B

H₀:       scritto anche come      H₀:

3 - per l’interazione A x B

H₀:      scritto anche come     

 

Abitualmente sono verificate tutte tre.

Ma l’analisi può essere limitata a una sola ipotesi, se l’interesse del ricercatore a rivolto a quell’unico problema.

 

Per effettuare i vari test F, dai dati devono essere calcolate 5 devianze:

(1) Totale,  (2) Tra Trattamenti,  (3) Tra blocchi,  (4) Interazione: Trattamenti per Blocchi,  (5) Errore.

 

Utilizzando le formule abbreviate, che in questo caso sono molto più semplici,

 

1 – La devianza totale () è

  e con i dati dell’esempio

 

 risulta  = 77.646,96

 e ha gdl =

 

La successiva Devianza tra le medie delle caselle non è richiesta per i test di significatività. Ma essa è utile per

-  meglio comprendere le formule successive,

-  arrivare rapidamente al calcolo delle altre devianze.

Inoltre le medie di casella servono per evidenziare gli effetti della interazione tra i due fattori (A x B).

 

Pertanto, dalla tabella dei dati riportata precedentemente, è opportuno ricavare le medie delle 9 caselle. In realtà le formule abbreviate utilizzano le somme. Ma in campioni bilanciati (nell'esempio  = 4), le somme e le medie forniscono le stesse informazioni sui rapporti tra le loro dimensioni

 

 

 

 La devianza tra caselle () è

 

 

 e con i dati dell’esempio

 

 

 risulta  = 59.416,21

 e ha gdl = .

 

Successivamente si calcolano le altre quattro devianze già indicate:

 

2 - La devianza tra materiali ()

 

 

  con i dati dell’esempio

 

 

 risulta  = 10.683,72

 e ha gdl = .

 

3 - La devianza tra temperature ()

 

 

  con i dati dell’esempio

 

 

 risulta  = 39.118,72

 e ha gdl = .

 

4 - La devianza d’interazione ()  Materiali x Temperature, che con la formula abbreviata è calcolata per differenza

 =  -  -

 se applicata ai dati dell’esempio

 = 59.416,21 – 10.683,72 – 39.118.72 = 9.613,77

 risulta  = 9.613,77

 e ha gdl = 8 – 2 – 2 = 4.

 

5 - La devianza d’errore (), sempre con la formula abbreviata, è anch’essa calcolata per differenza

 =  -   

Con i dati dell’esempio

 = 77.646,96 - 59.416,21 = 18.230,75

 risulta  18.230,75

 e ha gdl = 35 – 8 = 27.

 

(Per calcolare la devianza d’interazione e la devianza d’errore direttamente e non mediante le differenze, si rinvia ai paragrafi nei quali i metodi sono stati illustrati in modo dettagliato).

Per verificare i calcoli attraverso le proprietà additive e per impostare le analisi successive, è conveniente riportare le devianze () e i gradi di libertà () in una tabella

 

 

(I valori riguardanti le medie delle caselle sono stati scritti in corsivo per differenziarle, ricordando che molti programmi informatici abitualmente li omettono).

 

Dal rapporto tra le devianze e o rispettivi degree of freedom, si ricavano le varianze  (quarta colonna) e da esse i tre rapporti F (quinta colonna):

 

 

Dalla tabella dei valori critici, per i gradi di libertà corrispondenti, si ricavano le probabilità  che mostrano

- una significatività alta per i due fattori principali,

- la presenza di significatività anche per l’interazione Materiali per Temperature.

 

Nella interpretazione disciplinare dei risultati statistici, la significatività della interazione (Materiali x Temperatura) indica che

- le variazioni di temperatura hanno effetti differenti sui tre materiali.

Per una lettura più dettagliata e una spiegazione logica sono di aiuto

-   la tabella delle medie (Average output voltage)

-  la loro rappresentazione grafica, in funzione delle temperature (Temperature °F)

 riportate nella pagina successiva.

 

 

 

 

L’analisi combinata dei risultati statistici e l'osservazione dei valori medi conduce alle seguenti tre conclusioni:

1 - con probabilità  di errare, si può affermare che utilizzando i tre tipi di materiale si hanno effetti molto differenti sul voltaggio massimo delle batterie;

2 - con probabilità  di errare, si può sostenere che alle tre diverse temperature dell’esperimento (50° F, 65°F, 80°F) il voltaggio massimo delle batterie è molto differente;

3 - con probabilità  di errare, si può dichiarare che l’effetto della temperatura ai vari livelli è significativamente diverso nei differenti materiali testati.

La tabella e il grafico precedenti mostrano, ad esempio, che per una temperatura di 50°F il materiale di tipo 2 determina il voltaggio più alto, ma che a temperature superiori (65°F e 80°F) il materiale con il voltaggio massimo è quello di tipo 3.

 

Per analisi più dettagliate delle differenze sia tra le tre medie dei materiali, sia tra le tre medie delle temperature e anche per le nove medie dell’interazione (materiale per temperatura), occorre utilizzare i confronti multipli a priori oppure a posteriori (per approfondimenti di questi concetti si rinvia ai paragrafi relativi).

 

 

B – ANOVA II O MODELLO A EFFETTI RANDOM

L’analisi precedente può essere contestata. Probabilmente è errata.

Sussiste incertezza sulla sua validità, in quanto non sono state fornite tutte le informazioni necessarie per comprendere l’esatta finalità del test, dalla quale dipende la scelta dei tre livelli del fattore A e del fattore B.

I tre livelli del fattore A sono esattamente quelli che si vogliono analizzare con il test oppure

-  il numero di materiali utilizzabili è più alto e quei tre sono stati scelti casualmente?

In altri termini, lo scopo specifico dell’esperimento è di

-  verificare in generale se materiali differenti hanno effetti differenti sul voltaggio massimo?

In questo esempio, la stessa domanda può essere estesa anche alle tre temperature utilizzate. Si voleva verificare l’effetto di quelle tre temperature specifiche, oppure se

- variando la temperatura entro un intervallo di condizioni ambientali normali (ad esempio, tra 40°F  e 90°F), la temperatura ha effetti importanti?

 

 Se la risposta a questa ultima domanda è affermativa, in modo più specifico se la scelta delle tre temperature (50, 65 e 80 °F) è stata casuale e potevano essere utilizzate altre temperature entro l’intervallo prestabilito, certamente l’analisi statistica precedente è errata.

Ai dati presentati, è necessario applicare il modello a effetti random.

 

Questo lungo ragionamento per meglio chiarire le finalità dell’esperimento ha lo scopo di evidenziare che, soprattutto in questo settore della statistica,

- occorre esprimere con chiarezza l’ipotesi di lavoro, la domanda alla quale si vuole rispondere.

Ma sono risposte che solamente l’esperto che ha condotto l’esperimento può dare. Da questa semplice osservazione deriva la necessità che egli abbia conoscenze statistiche adeguate, per impostare l’esperimento in modo corretto.

 

Per passare dall’analisi a effetti fissi all’analisi a effetti random, si supponga ora che i tre materiali e le tre temperature di esercizio (50, 65 e 80 °F) siamo stati scelti casualmente entro un intervallo di variazione maggiore, ottenendo gli stessi risultati  conseguiti nell’esperimento precedente:

 

 

 

 

Come per gli effetti fissi, anche nell’analisi degli effetti random ogni singola osservazione  può essere descritta dal modello statistico lineare

 

 

 con  = 3,     = 3,     = 4,   

 

 Ma in questo caso, i quattro parametri del modello ,  ,  ,    sono variabili random.

Quindi hanno effetti nulli e presentano variabilità.

In modo più specifico, nel modello si assume che i quattro parametri analizzati

- siano distribuiti in modo normale e indipendente; quindi abbiano  media m = 0 e varianza = .

Con simbologia statistica, questo concetto è espresso con:

-   è  NID (),

-   è  NID (),

-   è  NID ()

-   è  NID ()

 dove NID = Normally and Indipendently Distributed

 

Ne deriva che

- la varianza di ogni osservazione è

 - ,  ,    e   sono le componenti della varianza (variance components)

 

Rispetto all’ANOVA a effetti fissi, cambiano anche le ipotesi da verificare.

Nel modello a effetti random, sono

1 - per i trattamenti o fattore A

H₀:  = 0

2 - per i blocchi o fattore B

H₀:  = 0

3 - per l’interazione A x B

H₀:  = 0

 

Per verificare queste ipotesi, si utilizzano

-  le stesse formule  dell’ANOVA a effetti fissi

- e si ottiene la stessa tabella di risultati,

 per quanto riguarda

-  le devianze,  i degree freedom,  le varianze.

 

Cambiano i  test F per i due effetti principali, ma non quello per l’interazione.

 

 

1 -  Per la verifica dell’ipotesi H₀:  = 0

 si effettua il test

 

 Con gdl uguali a  2 e 4 risulta significativo con probabilità

 

2 -  Per la verifica dell’ipotesi H₀:  = 0

 si effettua il test

 

 Con gdl uguali a  2 e 4  non risulta significativo.

 

3 -  Per la verifica della presenza d’interazione e quindi dell’ipotesi H₀:  = 0

 si effettua il solito test

 

Con gdl uguali a  4 e 27 risulta significativo con probabilità

 

L’interpretazione disciplinare dei risultati statistici ottenuti

- per l’interazione è che esiste variabilità tra le medie di caselle; quindi, se si analizzano gli effetti dei possibili materiali utilizzabili alle diverse temperature di esercizio, le potenze massime cambiano in modo differente;

- per il fattore A è che, tra tutti i materiali possibili, non esiste una differenza significativa,

- per il fattore B è che, tra le possibili temperature di esercizio delle batterie, esiste una differenza significativa nel voltaggio massimo.

 

Nel testo citato (pag. 136), Douglas Montgomery sottolinea che, come nel caso degli effetti fissi,

 -  questi test sono sempre unilaterali o a una coda (These are all upper-tail, one-tail tests),

 in quanto per risultare significativi

- la varianza al numeratore deve essere maggiore di quella al denominatore.

 

A questo fine, è utile ricordare che le tabelle F per l’ANOVA sono unilaterali.

Quindi si utilizza la probabilità a indicata. Il problema, come evidenziato nel capitolo relativo, si pone solamente per

- il test bilaterale di omoschedasticità tra due sole varianze,

 in quanto il test F è fondato sul rapporto tra la varianza maggiore e quella minore

senza che a priori sia noto quale delle due sia quella maggiore, quindi decidendo solamente sulla base dell’osservazione dei risultati campionari.

Nei test bilaterali di omoschedasticità,

-  per una probabilità a = 0.05 bilaterale si deve prendere il valore critico di a = 0.025.

 

Ritornando all’ANOVA II, la spiegazione logica della metodologia illustrata è fondata sui tre concetti seguenti:

1 – La varianza attesa per l’errore  (Expected Mean Squares) è

mentre la varianza attesa per l’interazione A x B  è

 quindi per verificare l’ipotesi H₀:  = 0 è appropriato

 il rapporto

 dove  ha i gradi di libertà di questo rapporto.

 

2 – La varianza attesa per il fattore B  è

 mentre la varianza attesa per l’interazione A x B  è

 quindi per verificare l’ipotesi H₀:  = 0 è appropriato

 il rapporto

 dove  ha i gradi di libertà di questo rapporto.

 

3 – La varianza attesa per il fattore A  è

 mentre la varianza attesa per l’interazione A x B  è

 quindi per verificare l’ipotesi H₀:  = 0 è appropriato

 il rapporto

 dove  ha i gradi di libertà di questo rapporto.

 

LE COMPONENTI DELLA VARIANZA E LORO INTERVALLO DI CONFIDENZA

Con  = 3,     = 3,     = 4, come nell’esempio sviluppato, dalle relazioni appena indicate per ogni singola varianza

 

 è possibile stimare le componenti della varianza (the variance components)

-  con il metodo dell’analisi della varianza (analysis of variance methods).

 

Ritornando ai dati dell’ultima tabella ANOVA II,

 

 

 con il metodo detto dell’analisi della varianza (analysis of varaince methods), appunto perché si serve  dei risultati riportati nella tabella dell’analisi della varianza per stimare  e ,

1 - da

     si ricava   

 

2 - da

    si ricava   

 

3 - da

     si ricava    

 

4 - da

     si ricava     

 

Il valore   è un risultato campionaria.

Il valore vero  è ricavato dalla stima dell’intervallo di confidenza (confidence interval estimate) mediante la distribuzione chi-quadrato,

poiché

 

 è distribuito come un  con gradi di libertà , cioè .

Per una spiegazione dettagliata delle modalità, si rinvia al paragrafo dedicato all’intervallo di confidenza di una varianza.

 

Il metodo dell’analisi della varianza, per ricavare la stima delle componenti della varianza, non richiede l’assunzione della normalità degli errori, ma solo che  e  siano gli stimatori quadratici non distorti minori, quindi che essi abbiano varianza minima.

 

Il metodo di stima dell’intervallo di confidenza della varianza d’errore non sempre può essere utilizzato anche per le altre varianze.

Con il metodo dell’analisi della varianza, può infatti avvenire che

- una componente della varianza risulti negativa, in quanto è una stima campionaria di un valore che dovrebbe essere uguale a 0.

Ma, per definizione essendo fondata sul quadrato di scarti dalla media, una componente della varianza non può essere negativa, per cui si assume che essa sia uguale a 0. E’ un approccio che intuitivamente ha un fascino logico, ma che a sua volta genera difficoltà teoriche nei calcoli successivi, in quanto altera le proprietà statistiche degli altri stimatori che nel loro calcolo utilizzano questa componente.

Una soluzione alternativa è ricorrere a metodi di stima delle componenti che sono sempre in un campo non negativo; ma a loro volta originano altre complicazioni, in quanto non sono più fondate sul modello lineare di additività delle componenti.

Per approfondimenti su questo settore della statistica, si rinvia al testo di Montgomery qui citato e all’articolo di S. R. Searle del 1971 Topics in Variance Component Estimation, pubblicato su Biometrics, Vol. 27, pp.1-76.

 

 

C – ANOVA III O MODELLO MISTO; SOLUZIONE STANDARD E ALTRE PROPOSTE

L’esempio analizzato in questo paragrafo si presta anche per una discussione sul modello misto dell’analisi della varianza (mixed model analysis of variance), se si suppone che

-   il fattore A (Materiali) sia fisso (ad esempio, esistono solamente quei tre materiali per costruire le batterie e si vogliono valutare i loro effetti specifici sul voltaggio massimo),

-   il fattore B (Temperature) sia random (ad esempio, la temperatura di esercizio delle batterie varia da 40 °F a 90 °F e per l’esperimento le tre utilizzate sono state scelte in modo casuale, per rispondere alla domanda generica che a temperature differenti il  voltaggio massimo è differente.)

 

Il modello statistico lineare è

con  = 3,     = 3,     = 4   e   dove

-   è un effetto fisso, tale che

-   è una variabile random NID (0, )

-  l’interazione  è una variabile random, distribuita in modo normale con media 0 e varianza  e la somma della componente dell’interazione per il fattore fisso è uguale a 0,  vale a dire

 

Questo ultima assunzione implica che gli elementi dell’interazione entro un particolare livello del fattore fisso non sono indipendenti,

poiché

Cov

 vale a dire che

- la covarianza tra  e  per  è zero  mentre  l’errore random  è NID (0, ).

 

In questo modello, per semplificare la formula che permette di calcolare la varianza attesa,

-  la varianza di  è definita come  più che .

L’assunzione  ha effetti anche sulle varianze attese, che possono essere scritte

 come

 

I loro  valori, ottenuti con l'ANOVA, sono riportati nella tabella successiva

 

 

Secondo le ipotesi espresse in precedenza, nel modello misto l’ipotesi nulla

1 - per i trattamenti o fattore A verte sulle medie; più esattamente è

H₀:       scritto anche come      H₀:

 e con i dati dell’esempio viene verificata

 mediante

 che ha gdl 2 e 4; non è significativa;

 

2 - per i blocchi o fattore B è

H₀:  = 0

 e viene verificata con

 

 che ha gdl 2 e 27; è altamente significativa;

 

(Nota Bene: L'aspetto particolare di questo test F è che per la significatività del fattore B, che è una variabile random,

-  al denominatore è utilizzata la varianza d'errore  

-  e non quella d'interazione  come nell'esempio del modello random precedente.

La causa è dovuta al fatto che, nella enunciazione delle ipotesi per questo test, l'interazione non è stata ritenuta indipendente dal fattore B.)

 

3 – per l’interazione A x B è

H₀:  = 0

 si viene verificata con

 che ha gdl 2 e 27; è significativa.

 

Le componenti della varianza ,   e   possono essere stimate usando il metodo dell’analisi della varianza, con esclusione di quella relativa al fattore fisso.

La soluzione (diversa da quella riportata per gli effetti random come  nel precedente test F)

è

 

 

 

Questo approccio generale può essere utilizzato per stimare le componenti della varianza in qualsiasi modello misto e rappresenta il modello standard.

Ma sono state proposte anche numerose soluzioni differenti, che si diversificano dalla precedente per le assunzioni sulle componenti random  e , vale a dire per le assunzioni che interessano un fattore principale e l’interazione.

 

Supponendo che

-  sia un effetto fisso, tali che ,

-  sia una variabile random con NID  (Normally and Indipendently Distributed),

-   siano gli effetti dell’interazione con NID  e indipendenti dall’effetto random ,

(annotando che in questo caso l’interazione è indipendente dal fattore B)

-  sia la componente di errore random con NID ,

 le varianze attese sono

 

Per evidenziare maggiormente la differenza con il modello procedente, osservare che prima

-  la varianza attesa del fattore B era

Nel caso ora in discussione, l’ipotesi nulla

-  per i blocchi o fattore B è sempre

H₀:  = 0

 ma viene verificata con

 

 che ha gdl 2 e 4; è significativa (P < 0.05)

Di norma in questo  modello, come in questo caso, il test risulta meno significativo.

In termini tecnici, si afferma che è più conservativo (in alcuni testi si dice anche che è meno liberale), rispetto al modello misto standard, poiché

-  la varianza d’interazione  è maggiore

- della varianza d’errore .

 

Con i dati dell’esempio, la componente della varianza per il fattore B, sempre ricorrendo al metodo dell’analisi della varianza,

 è

 

Questo ultimo modello e il precedente sono entrambi casi speciali del modello misto proposto da H. Scheffé

- nel 1956 con l’articolo A “Mixed Model” for the Analysis of Variance (pubblicato su Annals of Mathematical Statistics Vol. 27, pp.: 23-36)

-  e divulgato nel volume del 1959 The Analysis of Variance (edito da Wiley, New York),

Questo modello assume che ogni singola osservazione  può essere rappresentata da

 

 dove

 -  e   sono variabili random indipendenti.

Nella tabella dei dati sperimentali

 

 

 

 

-  la variabile  corrisponde alla media di ogni casella e la sua struttura è

 - mentre il suo valore atteso  è

 con

 e

 

 

Scheffé definisce la matrice di Covarianza per .

E’ possibile anche esprimere le varianze e le covarianze di  e  indirettamente, , specificando gli elementi di questa matrice.

Il modello di analisi statistica proposto da Scheffé è identico al precedente modello standard, proposto da Montgomery, con l’eccezione che in generale

 la statistica

 

 non sempre è distribuita come  quando l’ipotesi nulla  è vera.

 

Di fonte alla molteplicità dei modelli misti, si pone il problema della scelta.

Secondo Montgomery, che fa riferimento alla sua lunga esperienza, la maggior parte degli statistici tende a preferire il modello standard, che è anche quello più frequentemente utilizzato in letteratura. Se la correlazione presente nella componente random non è grande, allora sono appropriati entrambi i modelli e tra loro esistono solamente differenze piccole. Ma se la correlazione è grande, allora è più corretto utilizzare il modello di Scheffé.

In conclusione, la scelta tra i modelli dipende dai dati.

Per approfondimenti, si rinvia all’articolo di R. R. Hocking  del 1973 A discussion of the Two-Way Mixed Model (pubblicato su The American Statistician Vol. 27 No. 4, pp.: 148-152)