ANALISI DELLA VARIANZA a piu’ criteri di classificazione
11.8. POTENZA A PRIORI E A POSTERIORI NELL’ANOVA, CON I GRAFICI DI PEARSON E HARTLEY
I concetti e i metodi per stimare la potenza di un test, già illustrati nei capitoli precedenti con la distribuzione Z e la distribuzione t, prendono in considerazione un numero più alto di parametri nel caso di k campioni, senza per questo diventare molto più complessi. Per stimare la potenza di un test F nell’ANOVA, i metodi proposti negli ultimi decenni sono numerosi. In letteratura è possibile trovare presentazioni ampie e dettagliate, come il volume di J. Cohen del 1988 (Statistical Power Analysis for the Behavioral Sciences, 2nd edition Lawrence Erlbaum Associates, Hillsdale, New Jersey, pp. 567), che ne riassume il dibattito e i risultati. I programmi informatici più sofisticati iniziano a presentare anche questa opzione, tra gli output offerti, fornendo direttamente il valore 1-b della potenza del test. Tuttavia, - sia per comprendere i concetti che stanno alla base di questi metodi, - sia per individuare i parametri implicati nella stima della potenza di un test ANOVA, appare ancora utile rifarsi alle carte di E. S. Pearson e H. O. Hartley del 1951 (Charts for the power function for analysis of variance tests, derived from the non-central F-distribution. Biometrika, 38:112-130), che utilizzano la distribuzione F non-centrale. La presentazione successiva e le tabelle riportate sono tratte da questo articolo.
La distribuzione dei valori F per l’ANOVA è individuata da n1 e n2, determinati dai gdl della varianza tra e della varianza entro, quando l’ipotesi nulla H0 è vera. Ma quando H0 è falsa, il rapporto tra le due varianze assume una forma diversa, detta distribuzione F non centrale (noncentral F-distribution), che si allontana dalla precedente in funzione dalla distanza d, esistente tra le due o più medie a confronto (d = mmax - mmin). Di conseguenza, per identificare una distribuzione non centrale, ai due parametri n1 e n2 deve essere aggiunto un terzo, indicato con f e detto della non-centralità (noncentrality parameter), che dipende a sua volta dalla varianza tra trattamenti, dalla varianza d’errore e dai loro gdl. La potenza (1-b) del test F, che è collegata alla probabilità b di commettere l’errore di II Tipo (accettare l’ipotesi nulla H0 quando è falsa), dipende da queste caratteristiche di ogni distribuzione F non centrale.
I grafici di E. O. PEARSON e H. O. HARTLEY, riportati nelle pagine finali del capitolo, rappresentano una elaborazione delle tabelle scritte da P. C. Tang nel 1938 (The power function of the analysis of variance tests with tables and illustrations of their use, pubblicate su Statistical Research Memoirs Vol. 2, pp. 126 – 149 and tables) e sono di più facile lettura ed interpolazione. Sinteticamente le loro caratteristiche fondamentali sono: - I grafici sono 8; servono per stimare la potenza di un test ANOVA con un numero di medie che varia da 2 ad un massimo di 9. Ognuno è identificato dai gdl della varianza tra, indicati con n1, che variano da 1 a 8. - Ogni grafico riporta 2 famiglie di curve di potenza, corrispondenti a a = 0.05 e a = 0.01. - Entro ogni famiglia le curve sono 11, relative ai gdl della varianza d’errore; sono indicate con n2 e sono state tracciate solo quelle che hanno gdl 6, 7, 8, 9, 10, 12, 15, 20, 30, 60, ¥. Per altri gdl si deve ricorre all’interpolazione. - Dato un certo valore di f, riportato in ascissa, ogni curva (individuata appunto da n1, a, n2) permette di stimare la potenza 1-b, riportata in ordinata. - La scala di potenza 1-b è logaritmica per b, in modo da espandere i valori di potenza nella regione più importante e di uso più frequente, tra 0.80 e 0.99, facilitandone la lettura e l’interpolazione. - I valori di f, riportati in ascissa, dipendono da a e hanno un campo di variazione limitato, in quanto determinato dalle potenze relative. Essi variano nei diversi grafici, in quanto influenzate sensibilmente anche dal numero di gruppi a confronto (n1)
Nell’analisi della varianza ad un criterio, il valore di f può essere ottenuto a partire:
- dalle medie campionarie quando i campioni sono bilanciati con f =
- dai risultati dell’analisi della varianza con f = dove (per entrambe le formule) -
- n è il numero di dati di ogni gruppo, - p è il numero di gruppi, -
-
(Osservare che in entrambe le formule al numeratore compare la devianza tra trattamenti. Nelle formule successive, essa sarà valutata attraverso la differenza massima d tra le p medie a confronto).
Stimato f, per calcolare la potenza 1-b (o derivare da essa la probabilità b) mediante le curve di probabilità, è necessario determinare: - n1 che indica il grafico da scegliere, - a (uguale a 0.05 oppure a 0.01, poiché questi grafici non permettono altre opzioni) che indica la riga (tra le due riportate sulle ascisse) nella quale individuare il punto corrispondente al valore di f e il blocco di curve entro il grafico, - n2 (i gdl della varianza d’errore) che sulle 2 ordinate esterne indicano la curva (approssimata a partire da 11) dalla quale risalire al valore della potenza 1-b, partendo da quello di f riportato in ascissa.
ESEMPIO 1. In tre zone di una città, sono state effettuate 5 misurazioni del livello di benzopirene (ng/mc) presente nell’aria, con i seguenti valori medi
L’analisi della varianza ad un criterio, della quale si riportano i risultati,
non ha permesso di rifiutare l’ipotesi nulla. Infatti - il valore critico di F, con gdl 2 per il numeratore e 12 per il denominatore, per la probabilità a = 0.05 è 3,89 mentre il valore calcolato è 2,81; - in modo più preciso, il valore calcolato (2,81) corrisponde ad una probabilità a uguale a 0,20 per un test bilaterale. Domande: sulla base di questi dati, stimare la potenza (1-b) del test, per la significatività ad una probabilità a) a = 0.05 b) a = 0.01
Risposte Con la formula che utilizza le medie in campioni bilanciati
f = dove - -
-
si ottiene f =
f =
un valore di f uguale a 1,37.
Con la formula che ricorre ai risultati dell’ANOVA
f = dove -
-
si ottiene f =
un valore di f uguale a 1,37 (ovviamente identico al precedente). Successivamente, mediante il grafico, si passa dal valore di f a quello di 1-b, in modo indipendente per le due probabilità a = 0.05 e a = 0.01.
a) Per a = 0.05, con - n1 = 2 (secondo grafico), - il valore di f uguale a 1,37 letto nella riga per a = 0.05 (riga superiore nell’ascissa e blocco di curve a sinistra), all’incrocio con - n2 = 12, fornisce un valore di 1-b uguale a circa 0,45 (difficile da leggere con precisione per l’addensarsi del fascio di curve).
b) Per a = 0.01, con - n1 = 2 (stesso grafico), - il valore di f uguale a 1,37 letto nella riga per a = 0.01 (riga inferiore nell’ascissa e blocco di curve a destra) - con n2 = 12 fornisce un valore di 1-b uguale a circa 0,20.
In conclusione, l’analisi della potenza a posteriori del test con l’ANOVA permette di affermare che - esisteva una probabilità b del 55% di non rifiutare (erroneamente) l’ipotesi nulla, scegliendo un livello di significatività a = 0.05; - esisteva una probabilità b dell’80 % di non rifiutare (erroneamente) l’ipotesi nulla, scegliendo un livello di significatività a = 0.01.
Come hanno evidenziato i concetti illustrati con i due esempi e come mostra la formula generale sotto-riportata, f = dove -
- diminuisce con la riduzione di a, la probabilità di commettere l’errore di I Tipo, - aumenta al crescere di n, il numero di repliche per campione, - aumenta al crescere della differenza d esistente tra le medie, - diminuisce al crescere del numero p di gruppi a confronto, -
diminuisce
al crescere della varianza d’errore
Utilizzando i risultati precedenti come se fossero quelli di uno studio pilota, effettuato solo per programmare correttamente un successivo esperimento, quello che realmente interessa, è possibile l’analisi della potenza a priori. E’ la base del disegno sperimentale, insieme con il tipo di campionamento. Per le relazioni che esistono tra i vari parametri, è possibile rispondere ad alcune domande. Per la programmazione di un esperimento al quale si pensa di applicare l’analisi della varianza ad un criterio, le più importanti sono 3: - la differenza minima (d) che sarà possibile evidenziare; - il numero minimo di dati (n) che è necessario raccogliere per ogni gruppo, o il numero totale (N) di dati, ovviamente in campioni bilanciati; - il numero massimo di gruppi (p) che è possibile formare con il numero totale (N) prefissato.
La differenza minima significativa (d) può essere dedotta direttamente attraverso la relazione d = dopo avere -
stimato
p, - identificato il valore richiesto di f nel grafico, sulla base dei 4 parametri n1, n2, a, 1-b. Il numero minimo di dati (n) che è necessario raccogliere e il numero massimo di gruppi (p) che è possibile formare sono ricavabili direttamente attraverso il grafico. I metodi, con tutti i loro passaggi logici, sono illustrati nel successivo esempio 3.
ESEMPIO 2. Riprendendo i risultati discussi nell’esempio 1, si chiede: “Per ottenere la significatività alla probabilità a = 0.05 e con una potenza 1-b = 0.90 (la potenza del test è a discrezione del ricercatore, ma spesso si sceglie 1-b = 0.80, per la relazione standard di 1 a 4 della probabilità b rispetto ad a) a)
quale
era la differenza minima (d) che era possibile evidenziare con il
campione raccolto (quindi mantenendo invariati p, n, b)
quale
dovrebbe essere il numero minimo di dati (N) da
raccogliere, ovviamente da distribuire in campioni bilanciati (predeterminando d e mantenendo
invariati p, c)
quale
è il numero massimo di gruppi (p) che è possibile formare
(predeterminando N, d e mantenendo invariato
Risposte a) Per stimare la differenza minima d che è possibile dimostrare significativa, con - n = 5;
p = 3, - dapprima si richiede che dal grafico sia ricavato il valore di f individuato da - n1 = 2; a = 0.05; 1-b = 0,90; n2 = 12; - che risulta uguale a circa 2,30; - successivamente si calcola d,
d = che risulta uguale a 0,78. Nello studio pilota poteva risultare significativa, ai livelli a e b prescelti, una differenza superiore a 0,78 tra media maggiore e media minore. Infatti il test non è risultato significativo, poiché la differenza massima tra le tre medie era (2,652 –2,195) uguale a 0,457.
b) Per stimare il numero minimo di dati (N) che è necessario raccogliere, sempre con a = 0.05; 1-b = 0.90; p = 3,
- dapprima si deve definire la differenza minima d che si intende verificare come significativa: è la scelta più strettamente dipendente dalla discrezionalità del ricercatore e influenza molto le dimensioni del campione che sarà necessario raccogliere; è bene scegliere il valore di d sulla base del suo significato biologico, come già evidenziato in paragrafi precedenti (nell’esempio, si assume come importante una differenza minima d = 0,5) - successivamente si deve agire per tentativi, ipotizzando un numero n ragionevole per ogni campione (ad esempio, n = 8; superiore ai 5 dell’esperimento pilota, non significativo) - quindi stimare il valore di n2 che deriva da questa scelta (n2 = p × (n - 1) = 3 × (8 - 1) = 21) - e calcolare il valore di f f = che deriva dalle scelte appena effettuate
f =
- Infine, utilizzando il grafico n1 = 2 (poiché p = 3) - si stima la potenza 1-b di f = 1,86 per a = 0.05 e n2 = 21. - Nel grafico, il valore di 1-b risulta circa 0,80. E’ troppo basso rispetto alla potenza richiesta.
Non resta che aumentare n, ipotizzando ad esempio n = 12 per un secondo tentativo, mantenendo costanti tutti gli altri parametri - Il nuovo valore di f f = risulta uguale a 2,28
con n2 = 33 = - Sempre nel grafico n1 = 2 si stima la potenza 1-b di f = 2,28 per a = 0.05 e n2 = 33. - Il valore di 1-b risulta circa 0,92. Si avvicina a quanto ipotizzato, superandolo leggermente: quindi, si può concludere che servono almeno 11-12 dati per gruppo, in totale tra 33 e 36 distribuiti in modo bilanciato.
c) Per stimare il numero massimo p di gruppi che si possono formare, è necessario ricordare che all’aumentare del numero p di gruppi la potenza del test diminuisce, anche mantenendo costante il numero n di dati in ogni gruppo (quindi aumentando N). Supponendo di poter effettuare in totale 60 osservazioni (N = 60), per stimare il numero massimo p di gruppi che si possono formare, mantenendo invariati -
d = 0,5; a = 0.05; 1-b = 0.90; si procede per tentativi, in modo analogo a quanto fatto nella stima di n. - Dapprima, essendo 60 superiore al numero 36 stimato in precedenza, si supponga di voler formare 4 gruppi (p = 4), per cui n = 15. - Successivamente con f = si stima il valore di f f = che risulta uguale a 2,21. - Con il grafico n1 = 3 (poiché p = 4) - si stima la potenza 1-b di f = 2,21 per a = 0.05 e n2 = 56 = (60 - 4). - Nel grafico, il valore di 1-b risulta superiore al 0.96. E’ molto alto, superiore alla potenza richiesta di 0.90. E’ quindi possibile pensare di formare 5 gruppi, se l’estensione delle zone studiate è importante ai fini della ricerca. Ipotizzando p = 5, con N costante (60) si ha n = 12. Mantenendo costanti tutti gli altri parametri - il nuovo valore di f
f = risulta uguale a 1,77 - Successivamente, si stima la potenza 1-b di f = 1,77 per a = 0.05 e n2 = 55 (60 – 5). - Nel grafico n1 = 4 (poiché p = 5) il valore di 1-b risulta minore di 0,90. Poiché la potenza di quella seconda ipotesi è minore di quella prescelta, si può concludere che con 60 osservazioni il numero massimo di gruppi che si possono formare è 4, se la potenza del test non deve essere inferiore a 0.90.
Sempre nell’articolo di E. S. Pearson e H. O. Hartley del 1951 (Charts for the power function for analysis of variance tests, derived from the non-central F-distribution, Biometrika Vol. 38, pp. 112-130), il metodo presentato è esteso a vari disegni dell’analisi della varianza: - quello a due criteri di classificazione, con una osservazione per cella, - quello a due criteri di classificazione, con nij osservazioni per cella, - quello a quadrati latini.
Nel caso di due criteri di classificazione con una sola osservazione per cella, i metodi illustrati non variano, ricordando che possono essere applicati indipendentemente per ognuno dei due fattori, in modo analogo al test F per la significatività. Di conseguenza, il valore di f è calcolato nello stesso modo
f = ricordando che -
-
Come per la significatività, la potenza del test per i due fattori sarà quasi sempre differente, essendo determinata dalla loro varianza tra (quindi dalla differenza tra le medie) e dal diverso numero di dati.
Nel caso di due criteri di classificazione con nij osservazione per cella, occorre distinguere tra - effetti principali e - interazione. Per gli effetti principali, il metodo è identico a quello dell’analisi a due criteri con una sola osservazione. Per l’interazione, il cui la varianza relativa dipende dagli scarti tra le medie osservate e le medie attese sulla base delle medie di riga e di colonna, il valore di f è f =
Con i quadrati latini, si ritorna al caso di due criteri con una sola osservazione, prendendo in considerazione per ognuno dei tre fattori la varianza e i gdl relativi. Questo metodo è facilmente estensibile a disegni sperimentali più complessi, con tre o più fattori e con repliche, purché bilanciati.
Per la stima a priori - delle dimensioni N del campione, - della differenza minima d che è si vuole rendere significativa, - del numero massimo di livelli (p) di uno specifico fattore, i metodi sono uguali a quelli presentati, applicando gli accorgimenti appena descritti.
| |||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||
e 
sono rispettivamente
la media di ogni gruppo i e la media generale,
è la varianza
d’errore
è la varianza tra
trattamenti.
= 2,652; 
= 2,195; 
= 2,496 dalle
quali è stato ricavato
= 1,37
= 0,27
= 1,37
corrisponde alla
devianza tra trattamenti e la potenza 1-
,
n dall’esperimento pilota e
= 0,78
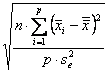
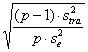
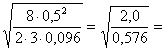1,86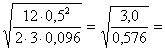
2,28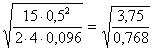
= 2,21
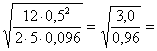1,77
è la varianza del
fattore che interessa, c on p medie a confronto e 