METODI NON
PARAMETRICI PER UN CAMPIONE
7.5. INTERVALLO DI
CONFIDENZA PER UNA PROBABILITA’ O FREQUENZA RELATIVA, SECONDO IL METODO DI
CLOPPER E PEARSON
La probabilità media (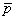 ) di un evento, calcolata su un campione
di dati raccolti in natura o con prove ripetute in laboratorio, è data dal
rapporto tra i casi positivi (B) e il numero totale di osservazioni (N)
) di un evento, calcolata su un campione
di dati raccolti in natura o con prove ripetute in laboratorio, è data dal
rapporto tra i casi positivi (B) e il numero totale di osservazioni (N)
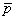 = B / N
= B / N
La sua deviazione standard (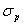 ) dipende dalla media
) dipende dalla media
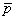 e da N, secondo la relazione
e da N, secondo la relazione
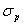 =
=
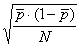
La varianza non è quindi misurata utilizzando la variabilità
campionaria delle repliche, ma è una funzione del valore medio.
Calcolata una probabilità o frequenza relativa dai dati di un campione,
spesso si pone il problema di conoscere la probabilità (p) vera o della
popolazione. E’ una domanda alla quale la statistica frequentista
risponde attraverso l’intervallo di confidenza.
Nel caso di campioni molto piccoli (N da 1 a 10), uno dei
metodi più semplici e rapidi per stimare l’intervallo di confidenza o
intervallo fiduciale è la procedura grafica, proposta da C. J. Clopper
e E. S. Pearson nel 1934 (nell’articolo The use of confidence
or fiducial limits illustrated in the case of binomial comparso su Biometrika
vol. 26, pp. 404-413).
Di questa procedura grafica vengono riportati solo i risultati e le
applicazioni.
Alcuni valori fondamentali (per
a = 0.01, 0.05,
0.10, 0.20) di una distribuzione bilaterale sono riportati nelle tabelle della
pagina successiva.
L’intervallo di confidenza alla probabilità 1 -
a della probabilità
media 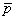 ,
compreso tra
,
compreso tra
il valore del limite inferiore pI (a/2) e
il valore del limite superiore pS (a/2)
può essere scritto come
Pp[ pI (a/2)
<
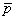 < pS (a/2)]
³ 1 -
a
< pS (a/2)]
³ 1 -
a
Per le applicazioni, le risposte sono fornite direttamente dalle
due tabelle seguenti.
Tabella dei limiti
di confidenza di una probabilità P = B/N (0.00
£ P
£ 1.00 )
calcolati con il
metodo grafico di Clopper e Pearson (1934)
N = dimensioni del
campione (da 1 a 10); B = numero di successi (varia da 0 a N)
a = probabilità
bilaterale; PI(a/2) = limite critico inferiore; PS(a/2) = limite
critico superiore
|
|
N = 1 |
N = 2 |
N = 3 |
N = 4 |
N = 5 |
B
|
|
pI() |
pS() |
pI() |
PS() |
pI() |
pS() |
pI() |
pS() |
pI() |
pS()
|
|
0 |
.010 |
.0000 |
.9950 |
.0000 |
.9293 |
.0000 |
.8290 |
.0000 |
.7341 |
.0000 |
.6534 |
|
|
.020 |
.0000 |
.9900 |
.0000 |
.9000 |
.0000 |
.7846 |
.0000 |
.6838 |
.0000 |
.6019 |
|
|
.050 |
.0000 |
.9750 |
.0000 |
.8419 |
.0000 |
.7076 |
.0000 |
.6024 |
.0000 |
.5218 |
|
|
.100 |
.0000 |
.9500 |
.0000 |
.7764 |
.0000 |
.6316 |
.0000 |
.5271 |
.0000 |
.4507 |
|
|
.200 |
.0000 |
.9000 |
.0000 |
.6838 |
.0000 |
.5358 |
.0000 |
.4377 |
.0000 |
.3690 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
.010 |
.0050 |
1.0000 |
.0025 |
.9975 |
.0017 |
.9586 |
.0013 |
.8891 |
.0010 |
.8149 |
|
|
.020 |
.0100 |
1.0000 |
.0050 |
.9950 |
.0033 |
.9411 |
.0025 |
.8591 |
.0020 |
.7779 |
|
|
.050 |
.0250 |
1.0000 |
.0126 |
.9874 |
.0084 |
.9057 |
.0063 |
.8059 |
.0051 |
.7164 |
|
|
.100 |
.0500 |
1.0000 |
.0253 |
.9747 |
.0170 |
.8647 |
.0127 |
.7514 |
.0102 |
.6574 |
|
|
.200 |
.1000 |
1.0000 |
.0513 |
.9487 |
.0345 |
.8042 |
.0260 |
.6795 |
.0209 |
.5839 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
.010 |
|
|
.0707 |
1.0000 |
.0414 |
.9983 |
.0294 |
.9706 |
.0229 |
.9172 |
|
|
.020 |
|
|
.1000 |
1.0000 |
.0589 |
.9967 |
.0420 |
.9580 |
.0327 |
.8944 |
|
|
.050 |
|
|
.1581 |
1.0000 |
.0943 |
.9916 |
.0676 |
.9324 |
.0527 |
.8534 |
|
|
.100 |
|
|
.2236 |
1.0000 |
.1353 |
.9830 |
.0976 |
.9024 |
.0764 |
.8107 |
|
|
.200 |
|
|
.3162 |
1.0000 |
.1958 |
.9655 |
.1426 |
.8574 |
.1122 |
.7534 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
.010 |
|
|
|
|
.1710 |
1.0000 |
.1109 |
.9987 |
.0828 |
.9771 |
|
|
.020 |
|
|
|
|
.2154 |
1.0000 |
.1409 |
.9975 |
.1056 |
.9673 |
|
|
.050 |
|
|
|
|
.2924 |
1.0000 |
.1941 |
.9937 |
.1466 |
.9473 |
|
|
.100 |
|
|
|
|
.3684 |
1.0000 |
.2486 |
.9873 |
.1893 |
.9236 |
|
|
.200 |
|
|
|
|
.4642 |
1.0000 |
.3205 |
.9740 |
.2466 |
.8878 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
.010 |
|
|
|
|
|
|
.2659 |
1.0000 |
.1851 |
.9990 |
|
|
.020 |
|
|
|
|
|
|
.3162 |
1.0000 |
.2221 |
.9980 |
|
|
.050 |
|
|
|
|
|
|
.3976 |
1.0000 |
.2836 |
.9949 |
|
|
.100 |
|
|
|
|
|
|
.4729 |
1.0000 |
.3426 |
.9898 |
|
|
.200 |
|
|
|
|
|
|
.5623 |
1.0000 |
.4161 |
.9791 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
.010 |
|
|
|
|
|
|
|
|
.3466 |
1.0000 |
|
|
.020 |
|
|
|
|
|
|
|
|
.3981 |
1.0000 |
|
|
.050 |
|
|
|
|
|
|
|
|
.4782 |
1.0000 |
|
|
.100 |
|
|
|
|
|
|
|
|
.5493 |
1.0000 |
|
|
.200 |
|
|
|
|
|
|
|
|
.6310 |
1.0000 |
CONTINUA NELLA PAGINA SEGUENTE
|
|
N = 6
|
N = 7 |
N = 8 |
N = 9 |
N = 10 |
B |
|
pI() |
pS() |
pI() |
PS() |
pI() |
pS() |
pI() |
pS() |
pI() |
pS() |
|
0 |
.010 |
.0000 |
.5865 |
.0000 |
.5309 |
.0000 |
.4843 |
.0000 |
.4450 |
.0000 |
.4113 |
|
|
.020 |
.0000 |
.5358 |
.0000 |
.4821 |
.0000 |
.4377 |
.0000 |
.4005 |
.0000 |
.3690 |
|
|
.050 |
.0000 |
.4593 |
.0000 |
.4096 |
.0000 |
.3694 |
.0000 |
.3363 |
.0000 |
.3085 |
|
|
.100 |
.0000 |
.3930 |
.0000 |
.3482 |
.0000 |
.3123 |
.0000 |
.2831 |
.0000 |
.2589 |
|
|
.200 |
.0000 |
.3187 |
.0000 |
.2803 |
.0000 |
.2501 |
.0000 |
.2257 |
.0000 |
.2057 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
.010 |
.0008 |
.7460 |
.0007 |
.6849 |
.0006 |
.6315 |
.0006 |
.5850 |
.0005 |
.5443 |
|
|
.020 |
.0017 |
.7057 |
.0014 |
.6434 |
.0013 |
.5899 |
.0011 |
.5440 |
.0010 |
.5044 |
|
|
.050 |
.0042 |
.6412 |
.0036 |
.5787 |
.0032 |
.5265 |
.0028 |
.4825 |
.0025 |
.4450 |
|
|
.100 |
.0085 |
.5818 |
.0073 |
.5207 |
.0064 |
.4707 |
.0057 |
.4291 |
.0051 |
.3942 |
|
|
.200 |
.0174 |
.5103 |
.0149 |
.4526 |
.0131 |
.4062 |
.0116 |
.3684 |
.0105 |
.3369 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
2 |
.010 |
.0187 |
.8564 |
.0158 |
.7970 |
.0137 |
.7422 |
.0121 |
.6926 |
.0109 |
.6482 |
|
|
.020 |
.0268 |
.8269 |
.0227 |
.7637 |
.0197 |
.7068 |
.0174 |
.6563 |
0155 |
.6117 |
|
|
.050 |
.0433 |
.7772 |
.0367 |
.7096 |
.0319 |
.6509 |
.0281 |
.6001 |
.0252 |
.5561 |
|
|
.100 |
.0628 |
.7287 |
.0534 |
.6587 |
.0464 |
.5997 |
.0410 |
.5496 |
.0368 |
.5069 |
|
|
.200 |
.0926 |
.6668 |
.0788 |
.5962 |
.0686 |
.5382 |
.0608 |
.4901 |
.0545 |
.4496 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
3 |
.010 |
.0663 |
.9337 |
.0553 |
.8823 |
.0475 |
.8303 |
.0416 |
.7809 |
.0370 |
.7351 |
|
|
.020 |
.0847 |
.9153 |
.0708 |
.8577 |
.0608 |
.8018 |
.0534 |
.7500 |
.0475 |
.7029 |
|
|
.050 |
.1181 |
.8819 |
.0990 |
.8159 |
.0852 |
.7551 |
.0749 |
.7007 |
.0667 |
.6525 |
|
|
.100 |
.1532 |
.8468 |
.1288 |
.7747 |
.1111 |
.7108 |
.0978 |
.6551 |
.0873 |
.6066 |
|
|
.200 |
.2009 |
.7991 |
.1696 |
.7214 |
.1469 |
.6554 |
.1295 |
.5994 |
.1158 |
.5517 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
.010 |
.1436 |
.9813 |
.1177 |
.9447 |
.0999 |
.9001 |
.0868 |
.8539 |
.0768 |
.8091 |
|
|
.020 |
.1731 |
.9732 |
.1423 |
.9292 |
.1210 |
.8790 |
.1053 |
.8290 |
.0932 |
.7817 |
|
|
.050 |
.2228 |
.9567 |
.1841 |
.9010 |
.1570 |
.8430 |
.1370 |
.7880 |
.1216 |
.7376 |
|
|
.100 |
.2713 |
.9372 |
.2253 |
.8712 |
.1929 |
.8071 |
.1687 |
.7486 |
.1500 |
.6965 |
|
|
.200 |
.3332 |
.9074 |
.2786 |
.8304 |
.2397 |
.7603 |
.2104 |
.6990 |
.1876 |
.6458 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
.010 |
.2540 |
.9992 |
.2030 |
.9842 |
.1697 |
.9525 |
.1461 |
.9132 |
.1283 |
.8717 |
|
|
.020 |
.2943 |
.9983 |
.2363 |
.9773 |
.1982 |
.9392 |
.1710 |
.8947 |
.1504 |
.8496 |
|
|
.050 |
.3588 |
.9958 |
.2904 |
.9633 |
.2449 |
.9148 |
.2120 |
.8630 |
.1871 |
.8129 |
|
|
.100 |
.4182 |
.9915 |
.3413 |
.9466 |
.2892 |
.8889 |
.2514 |
.8313 |
.2224 |
.7776 |
|
|
.200 |
.4897 |
.9826 |
.4038 |
.9212 |
.3446 |
.8531 |
.3010 |
.7896 |
.2673 |
.7327 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
.010 |
.4135 |
1.0000 |
.3151 |
.9993 |
.2578 |
.9863 |
.2191 |
.9584 |
.1909 |
.9232 |
|
|
.020 |
.4642 |
1.0000 |
.3566 |
.9986 |
.2932 |
.9803 |
.2500 |
.9466 |
.2183 |
.9068 |
|
|
.050 |
.5407 |
1.0000 |
.4213 |
.9964 |
.3491 |
.9681 |
.2993 |
.9251 |
.2624 |
.8784 |
|
|
.100 |
.6070 |
1.0000 |
.4793 |
.9927 |
.4003 |
.9536 |
.3449 |
.9022 |
.3035 |
.8500 |
|
|
.200 |
.6813 |
1.0000 |
.5474 |
.9851 |
.4618 |
.9314 |
.4006 |
.8705 |
.3542 |
.8124 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
.010 |
|
|
.4691 |
1.0000 |
.3685 |
.9994 |
.3074 |
.9879 |
.2649 |
.9630 |
|
|
.020 |
|
|
.5179 |
1.0000 |
.4101 |
.9987 |
.3437 |
.9826 |
.2971 |
.9525 |
|
|
.050 |
|
|
.5904 |
1.0000 |
.4735 |
.9968 |
.3999 |
.9719 |
.3475 |
.9333 |
|
|
.100 |
|
|
.6518 |
1.0000 |
.5293 |
.9936 |
.4504 |
.9590 |
.3934 |
.9127 |
|
|
.200 |
|
|
.7197 |
1.0000 |
.5938 |
.9869 |
.5099 |
.9392 |
.4483 |
.8842 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
.010 |
|
|
|
|
.5157 |
1.0000 |
.4150 |
.9994 |
.3518 |
.9891 |
|
|
.020 |
|
|
|
|
.5623 |
1.0000 |
.4560 |
.9989 |
.3883 |
.9845 |
|
|
.050 |
|
|
|
|
.6306 |
1.0000 |
.5175 |
.9972 |
.4439 |
.9748 |
|
|
.100 |
|
|
|
|
.6877 |
1.0000 |
.5709 |
.9943 |
.4931 |
.9632 |
|
|
.200 |
|
|
|
|
.7499 |
1.0000 |
.6316 |
.9884 |
.5504 |
.9455 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
.010 |
|
|
|
|
|
|
.5550 |
1.0000 |
.4557 |
.9995 |
|
|
.020 |
|
|
|
|
|
|
.5995 |
1.0000 |
.4956 |
.9990 |
|
|
.050 |
|
|
|
|
|
|
.6637 |
1.0000 |
.5550 |
.9975 |
|
|
.100 |
|
|
|
|
|
|
.7169 |
1.0000 |
.6058 |
.9949 |
|
|
.200 |
|
|
|
|
|
|
.7743 |
1.0000 |
.6631 |
.9895 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
.010 |
|
|
|
|
|
|
|
|
.5887 |
1.0000 |
|
|
.020 |
|
|
|
|
|
|
|
|
.6310 |
1.0000 |
|
|
.050 |
|
|
|
|
|
|
|
|
.6915 |
1.0000 |
|
|
.100 |
|
|
|
|
|
|
|
|
.7411 |
1.0000 |
|
|
.200 |
|
|
|
|
|
|
|
|
.7943 |
1.0000 |
Ad esempio
1) assumendo di avere avuto una risposta positiva su 4
tentativi (N = 4 e B = 1),
l’intervallo fiduciale del valore medio
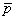 uguale a 0,25 è
compreso
uguale a 0,25 è
compreso
- tra 0,0063 e 0,8059 alla probabilità
a = 5% e
- tra 0,0127 e 0,7514 alla probabilità
a = 10%;
2) assumendo 4 risposte positive su 8 tentativi (N = 8 e B = 4),
l’intervallo fiduciale del valore medio
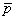 uguale a 0,50 è compreso
uguale a 0,50 è compreso
- tra 0,1570 e 0,8430 alla probabilità
a = 5% e
- tra 0,1929 e
0,8071 alla probabilità
a = 10%.
Con il metodo di
Clopper e Pearson, l’intervallo fiduciale è simmetrico solo per i valori medi
di 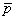 uguali a
0,50.
uguali a
0,50.
ESEMPIO. Per
stimare la diffusione geografica di una specie, sono stati campionati cinque
siti e la specie è stata trovata in due. Quale è la percentuale di presenza
p reale di questa
specie alla probabilità
a = 0.05, considerando l’universo dei siti?
Risposta. Il
campione è di dimensioni estremamente ridotte. Quindi per stimare l’intervallo
di confidenza è utile ricorrere alla tabella costruita con il metodo grafico di
Clopper-Pearson.
Per N uguale
a 5 e B uguale a 2 (corrispondente ad una
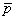 media di 0,4), alla probabilità
a = 0.05 nella
tabella viene riportato un intervallo di confidenza compreso tra 0,0527 e
0,8534.
media di 0,4), alla probabilità
a = 0.05 nella
tabella viene riportato un intervallo di confidenza compreso tra 0,0527 e
0,8534.
Tradotto in
percentuale, si può affermare che, con probabilità pari al 95%, la frequenza
reale
p di siti in cui è
presente la specie studiata varia tra 5,27% e 85,34%.
E’ importante
osservare che, rispetto al valore medio del campione (0,40), la
distribuzione non è simmetrica.
Per grandi
campioni, (anche se non è mai definito chiaramente il confine tra
campioni piccoli e grandi) si può ricorrere alla distribuzione normale,
essendo la varianza definita dalla media (e quindi nota), come già presentato
nel capitolo IV. La frequenza (p) reale o della popolazione si trova, con
probabilità 1-a,
entro l’intervallo
p =
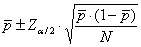
E’ una
distribuzione bilaterale; di conseguenza,
-
alla
probabilità complessiva
a = 0.05 in ognuna delle due code si deve prendere
a = 0.025 alla quale
corrisponde un valore di Z uguale a 1,96;
-
alla
probabilità complessiva
a = 0.01 in ognuna delle due code si deve prendere
a = 0.005 alla quale
corrisponde un valore di Z uguale a 2,58 (più esattamente 2,576).
ESEMPIO. Nelle
misure d’inquinamento dell’aria, in una città su 25 zone campionate il limite
di legge è stato superato in 6 casi. Quale è la frequenza reale
p di superamento dei
limiti di legge, alla probabilità
a = 0.05?
Risposta. Con
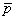 = 6/25 = 0,24 N
= 25 Z = 1,96 alla probabilità
a = 0.05 bilaterale,
= 6/25 = 0,24 N
= 25 Z = 1,96 alla probabilità
a = 0.05 bilaterale,
si ottiene un
intervallo fiduciale della media reale
p =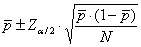 =
=
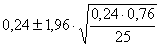 = 0,24
± 0,1674
= 0,24
± 0,1674
che varia
-
da
un limite inferiore uguale a 0,0726 (0,24 – 0,1674)
-
a
un limite superiore uguale a 0,4074 (0,24 + 0,1674).
La frequenza reale di superamento dei
limiti di legge, stimata con un campione di 25 osservazioni in una media pari a
24%, alla probabilità
a = 0.05 varia tra 7,26% e 40,74%.