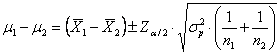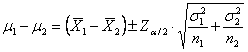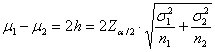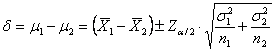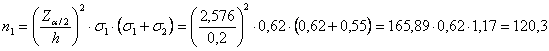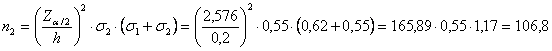VERIFICA DELLE IPOTESI

TEST PER UN CAMPIONE SULLA TENDENZA CENTRALE CON VARIANZA NOTA

E TEST SULLA VARIANZA

CON INTERVALLI DI CONFIDENZA

 

 

 

4.12. STIMA DELLA DIFFERENZA TRA DUE MEDIE CON UN ERRORE O UN INTERVALLO DI CONFIDENZA PREFISSATI, NEL CASO DI VARIANZA NOTA

 

 

In varie condizioni sperimentali, al ricercatore è richiesto non di effettuare un test di confronto sulla significatività della differenza tra le due medie come nei paragrafi precedenti, ma solamente

-  di calcolare la differenza reale d tra le due medie vere ,

-  con la precisione minima desiderata o l’errore massimo prestabilito.

 

Sebbene apparentemente simili ai test precedenti sulla significatività della differenza tra due medie,  queste stime sulla precisione della differenza tra due medie sono in realtà nettamente differenti, poiché in questo caso

-  nella stima di , le dimensioni minime dei due campioni,

-  non è implicato il rischio , ma solamente quello , in quanto non si tratta di un confronto.

 

Il problema è risolvibile partendo dai concetti sull’intervallo di confidenza della differenza

.

Sempre nelle condizioni di validità illustrate per la significatività della differenza tra le medie di due campioni indipendenti, che si riferiscono soprattutto alla normalità delle due distribuzioni,

- i limiti  e  dell’intervallo di confidenza (confidence interval in italiano tradotto anche con intervallo di fiducia o intervallo fiduciale) della differenza reale tra le medie di due campioni indipendenti

- alla probabilità a predeterminata sono calcolati con due formule differenti, (1) se le varianze sono uguali oppure (2) differenti.

 

1 – Quando le varianze sono uguali (), i limiti  e  della differenza tra le due medie vere

sono

 

2 – Quando le varianze diverse  (), i limiti  e  della differenza tra le due medie

sono

 

Con questa ultima formula, la lunghezza dell’intervallo intorno alla differenza tra le due medie (), indicata con , alla probabilità a

- è ricavata da

 

Da essa si deduce che, affinché la differenza  calcolata dai dati campionari rispetto alla differenza   abbia un errore non superiore a , alla probabilità a richiesta,

-  la dimensione del campione 1

 deve essere almeno

 

-  la dimensione del campione 2

 deve essere almeno

 

ESEMPIO  1 (CALCOLO DELL’INTERVALLO).  Una rapida analisi preliminare di pochi campioni sulla quantità di principio attivo immesso nel farmaco da una ditta concorrente in due tempi differenti (indicati rispettivamente con 1 e 2) ha dato i seguenti risultati:

 

= 63,516      = 0,62       = 5

= 62,548       = 0,55       = 4

 

Quale è la differenza () tra le due medie reali, alla probabilità a = 0.01?

 

Risposta. Assumendo le due deviazioni standard campionarie  e  come stime di quelle vere  e  , si può utilizzare la formula

Con i dati riportati e

- per la probabilità  = 0.01 bilaterale con  Z = 2,576

 dalla relazione

 e

 

 si ricava che alla probabilità  prefissata la differenza reale  d è compresa tra

- il limite inferiore L₁ = -0,038  

- il limite inferiore L₂ = +1,974  

 

ESEMPIO 2  (CALCOLO DI  PER L’ERRORE PRESTABILITO).   In un prodotto industriale che quasi sempre richiede stime molto precise, un campo di variazione della differenza reale d che oscilla tra il vantaggio di un campione (L₁ = -0,038) e il vantaggio dell’altro (L₂ = +1,974), come calcolato nell’esempio precedente, può essere ritenuto eccessivo ai fini pratici.

Per ottenere una misura della differenza tra le due medie che si discosti da quella reale d di una quantità  non superiore a 0,2 unità, con probabilità a = 0.01, quanti dati () sono necessari in ognuno dei due campioni?

 

Risposta. Assumendo le due deviazioni standard campionarie = 0,62  e   = 0,55 come stime di quelle della popolazione e con gli altri parametri indicati nella domanda, quindi con

-   = 0,62   e    = 0,55

-   = 0,2

-  Z = 2,576  per la probabilità  = 0.01 bilaterale

 

1 - la dimensione del campione 1  deve essere

 

 

  almeno uguale o superiore a  = 121

2 -  la dimensione del campione 2  deve essere

 

 

 almeno uguale o superiore a  = 107.

 

Nella presentazione di questi metodi, si è assunto che sia nota la varianza  delle due popolazioni, dalle quali sono stati estratti i due campioni. In realtà, nella prassi della ricerca spesso questa varianza vera  non è nota e le uniche informazioni disponibili sono i dati campionari raccolti. Pertanto, come stima migliore della varianza  della popolazione, si deve utilizzare la varianza campionaria .

Questa sostituzione del valore campionario al posto di quello vero  ha conseguenze molto importanti:

-  non  è più possibile utilizzare la distribuzione normale ridotta  

-  ma occorre la distribuzione  di Student, il cui uso è spiegato in un capitolo successivo.

Il calcolo di  diventa un po’ più complesso, in quanto il valore di  dipende da quello di , che a sua volta dipende da  o meglio dai suoi gradi di libertà. La soluzione è ottenuta in modo iterativo, con approssimazioni successive, seguendo le modalità spiegate nel capitolo sul test t di Student.

 

Il calcolo di  con , come effettuato in questo paragrafo per avere una differenza con una precisione prestabilita, è un metodo approssimato. E’ detto anche metodo asintotico, in quanto è valido per campioni grandi, poiché nei modelli matematici è richiesto che essi siano tendenzialmente infiniti.

Ma questo metodo con  è veloce e il risultato è vicino a quello più corretto ottenuto con , sempre quando  è abbastanza grande.

 

Nella pratica sperimentale, per queste analisi un campione è ritento grande quando  ³ 30.