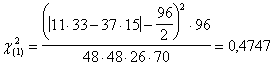|
CAP III - ANALISI DELLE FREQUENZE
3.12. ESERCIZI SVOLTI PER DATI IN TABELLE DI CONTINGENZA
ESERCIZIO 1. Per lo studio di frequenze alleliche del marcatore genetico ossidasi in popolazioni naturali di faggio di 4 differenti località dell’Appennino (Abetone, Pisanino, Pradarena, Pradaccio), sono state rilevate le frequenze di 3 alleli. Le frequenze osservate sono quelle riportate nella tabella sottostante.
FREQUENZE OSSERVATE
Esiste una differenza significativa nella distribuzione delle 3 frequenze alleliche? Si può sostenere che esiste associazione tra località e frequenze alleliche, per cui i 3 alleli non hanno la stessa distribuzione percentuale nelle 4 località?
Risposta. Dai totali marginali delle frequenze osservate, si calcolano le frequenze che dovremmo attenderci se fosse vero che non esiste differenza tra le percentuali dei 3 alleli nelle 4 località (distribuzione attesa, nella condizione che H0 sia vera).
FREQUENZE ATTESE SECONDO L’IPOTESI NULLA
Con la formula generale (Oss. - Att)2/ Att. si calcola il valore del c2, che avrà 6 gradi di libertà.
Si ottiene un chi
quadrato con 6 gradi Il valore risulta molto alto; la probabilità a che sia casuale è molto piccola, inferiore a 0,0001. Si conclude che esiste una differenza altamente significativa, fra le distribuzioni percentuali dei 3 alleli nelle 4 località. Per una lettura più dettagliata del test, sarebbe utile valutare quanto ogni casella contribuisce al valore complessivo del chi quadrato. Il confronto tra la distribuzione osservata e quella attesa evidenzia che, rispetto alla media delle 4 zone, all’Abetone e al Pisanino si ha un eccesso dell’allele 2 e una carenza dell’allele 1 e dell’allele 3, mentre al Pradaccio e a Pradarena si ha un eccesso degli alleli 1 e 3 e una carenza dell’allele 2.
ESERCIZIO 2. Si sono sottoposti dei cloni di Daphnia magna a quattro diversi trattamenti o regimi alimentari. Dopo 39 giorni si è fatto un bilancio complessivo di quanti sono stati i morti (e i sopravvissuti) in ogni campione. Si intende verificare se il tasso di mortalità è uguale per i 4 diversi trattamenti. Le differenze riscontrate sono dovute al caso, oppure sono imputabili al diverso trattamento alimentare?
FREQUENZE OSSERVATE
Risposta. Si calcolano le frequenze attese FREQUENZE ATTESE SECONDO L’IPOTESI NULLA
e successivamente, attraverso la formula generale, il valore del chi quadrato con 3 gradi di libertà
Si ottiene un valore Non è possibile rifiutare l’ipotesi nulla: non è dimostrato che i 4 trattamenti determinino una mortalità significativamente differente.
ESERCIZIO 3. Nella tabella seguente, sono riportati i risultati di un esperimento sulla schiusa di uova di Heterocypris incongruens, mantenute a diverse condizioni di temperatura.
FREQUENZE OSSERVATE
Trarre le conclusioni.
Risposta. Si calcolano le frequenze attese FREQUENZE ATTESE SECONDO L’IPOTESI NULLA
e attraverso la formula generale si può computare il valore complessivo del chi quadrato,
con il contributo fornito da ogni casella
(OSS. - ATT.)2 / ATT PER OGNI CASELLA
Il valore del I contributi maggiori sono forniti dalle due temperature estreme. Alla temperatura più bassa (16° C) il numero di uova che non si sono schiuse è molto maggiore, mentre alla temperatura più alta (28° C) è molto minore delle frequenze attese, se fosse stata vera l’ipotesi nulla che la temperatura non influisce. Alla temperatura intermedia (24° C), la percentuale di uova schiuse è molto vicina alla media dei 3 esperimenti.
ESERCIZIO 4. Si sono mantenute per 24 ore in due soluzioni acquose, contenenti uguale concentrazione di rame, due gruppi formati da 48 individui ciascuno, di 2 specie di protozoi: Euplotes patella e Paramecium caudatum. Alla fine dell’esperimento, si è contato il numero di individui morti in ognuno dei due campioni. I risultati sono riportati nella tabella sottostante. Verificare se la percentuale di decessi è diversa per le 2 specie, sottoposte alle medesime condizioni d’inquinamento.
FREQUENZE OSSERVATE
Risposta. E’ una tabella di contingenza 2 x 2 . Calcolando il chi-quadro, che avrà 1 g.d.l., con la formula rapida
si ottiene un valore uguale a 0, 843.
Una obiezione al risultato può essere che il numero totale di osservazioni non può essere considerato grande. In queste condizioni, a scopo cautelativo e quindi per una maggiore attendibilità delle conclusioni, è conveniente ricorrere al calcolo del chi quadrato con la correzione di YATES per la continuità
che (con un valore uguale a 0,4747) si dimostra più conservativa.
Con questi dati, è possibile utilizzare anche il metodo del log likelihood ratio o G2:
G2 = 2×{[ 11×ln(11) + 37×ln(37) + 15×ln(15) + 33×ln(33) + 96×ln(96)] - - [ 48×ln(48) + 48×ln(48) + 26×ln(26) + 70×ln(70)]} =
G2 = 2×{[(11x2,398)+(37x3,611)+(15x2,708)+(33x3,497)+(96x4,564)]- - [(48x3,871)+(48x3,871)+(26x3,258)+(70x4,248)]}=
G2 = 2×(754,104 - 753,742) = 2 x 0,362 = 0,724
Il valore del 2 è piccolo anche con questo metodo. E’ simile a quelli prima calcolati; è nettamente inferiore al valore critico di 3,83 corrispondente alla probabilità a = 0.05. Le variazioni riscontrate rientrano quindi fra quelle imputabili solo al caso. Non è possibile dimostrare che le due specie hanno reagito in modo differente alla stessa concentrazione di rame.
VALORI CRITICI DELLA DISTRIBUZIONE c2 (con gdl da 1 a 30)
(segue) VALORI CRITICI DELLA DISTRIBUZIONE c2 (con gdl da 31 a 60)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||