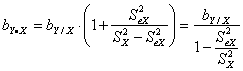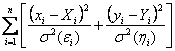|
LA REGRESSIONE LINEARE MODELLO II E LEAST-PRODUCTS. IL CONFRONTO TRA DUE METODI QUANTITATIVI.
24.6. LA FORMULA RAPIDA DI MANDEL E LA REGRESSIONE LEAST-PRODUCTS DI YORK.
Nell’anno 1964 J. Mandel nel volume The Statistical Analysis of Experimental Data (pubblicato da John Wiley and Sons, New York, NY) a pag. 290-291 propone due formule abbreviate per passare direttamente - dal coefficiente
angolare
dove - - Per questo
passaggio da un coefficiente angolare all’altro, è sufficiente calcolare la
varianza (
La formula di Deming è fondata - non sul presupposto
che la varianza del metodo - ma sul concetto
più generale che il rapporto
Tuttavia anche questa ipotesi, in varie situazioni sperimentali, è lontana dalla realtà. Le due varianze hanno un rapporto che si modifica entro il campo di variazione delle osservazioni. Nell’anno 1966 J. York nell’articolo Least squares fitting of a straight-line (pubblicato su Can. J. Phys. Vol. 44, pp.: 1079 – 1086) ha proposto una soluzione che consiste nel ridurre al minimo la funzione
dove - - con
In questa formula, le due varianze al denominatore sono calcolate entro ogni gruppo e sono in realtà dei fattori pesati. E’ un metodo che generalizza la precedente proposta di Deming. La soluzione è raggiunta attraverso un processo iterativo, per il quale occorre disporre del programma informatico.
| |
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |