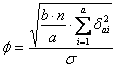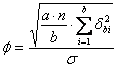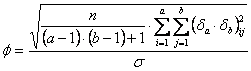|
IL DISEGNO SPERIMENTALE: CAMPIONAMENTO, PROGRAMMAZIONE DELL’ESPERIMENTO E POTENZA
23.10. IL DISEGNO SPERIMENTALE FATTORIALE SEMPLICE (DUE FATTORI CON INTERAZIONE): CALCOLO DELLA POTENZA A POSTERIORI
Quando vuole analizzare un esperimento con due o più fattori a vari livelli, spesso il ricercatore è interessato a valutare anche l’effetto della loro combinazione, chiamata interazione, con un termine tecnico. Ad esempio, se intende valutare gli effetti di due o più farmaci (fattore sperimentale) eliminando gli effetti dell’età e del sesso (fattori sub-sperimentali) può essere interessato a valutare anche se il farmaco mediamente migliore è tale per tutte le età e entrambi i sessi, oppure se per qualche età o per un sesso il farmaco che fornisce le risposte migliori sia differente. Data la ricaduta medica e commerciale di tale risposte, spesso l’interazione rappresenta lo scopo più importante di una analisi statistica. Il caso più semplice di interazione, che permette una interpretazione chiara e non equivoca dei risultati, è presente nel disegno fattoriale a due fattori con repliche
Ad esso si limita l’illustrazione dei metodi, come già nei capitoli dedicati all’analisi della varianza. Ricordando che occorrono almeno due repliche per casella e assumendo di utilizzare il caso più semplice di un numero di replicazioni costante in ogni casella, si ipotizzi un disegno sperimentale rappresentato nella tabella precedente con - 4 livelli nei
trattamenti (A, B, C, D): - 3 livello nei
blocchi (I, II,III): - 2 repliche per
ogni combinazione blocco x trattamento:
Il calcolo del
parametro I - della differenza tra le medie dei trattamenti, detto effetto principale A, II - della differenza tra le medie dei blocchi, detto effetto principale B, III - dell’interazione AB.
I - Per l’effetto
principale A la formula del parametro
con - - -
Tale formula per il
calcolo di 1) se si considera la differenza massima tra una media e tutte le altre, che sono tra loro uguali, si utilizza la formula
2) se le si utilizza la formula
II - Per l’effetto
principale B la formula del parametro
con - - -
Tale formula per il
calcolo di 1) se si considera la differenza massima tra una media e tutte le altre, che sono tra loro uguali, si utilizza la formula
2) se le si utilizza la formula
III - Per l’interazione
AB la formula del parametro
con - - - Come ampiamente descritto
nel capitolo relativo all’interazione tra due fattori, la quantità Nell’ipotesi H1
che una delle interazioni sia uguale a
ESEMPIO 1 (POTENZA
PER I TRATTAMENTI) Nel disegno sperimentale presentato, valutare la potenza del
test per i trattamenti per
Risposta. Se nell’ipotesi H1 si prende in considerazione la differenza reale esistente tra la media minore e la media maggiore
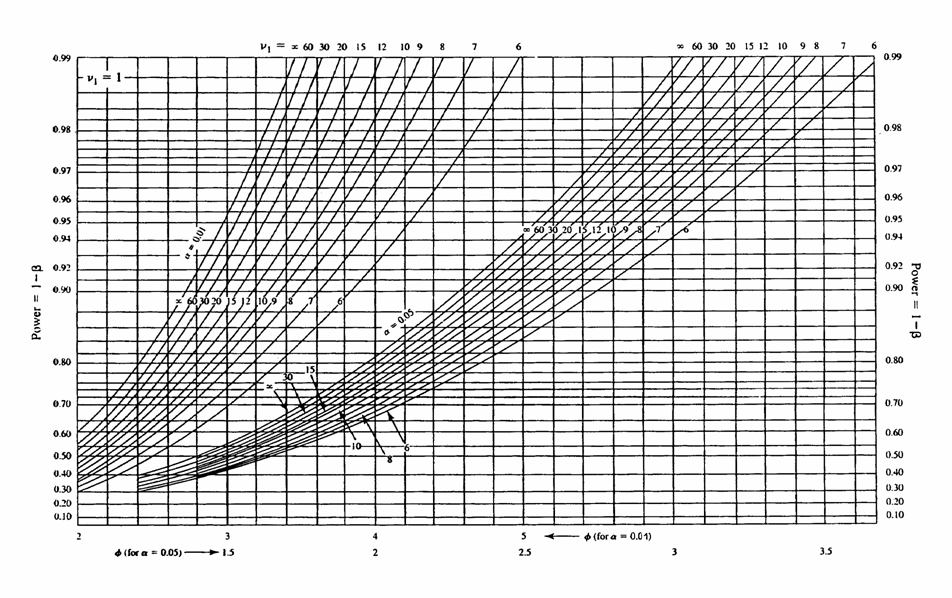
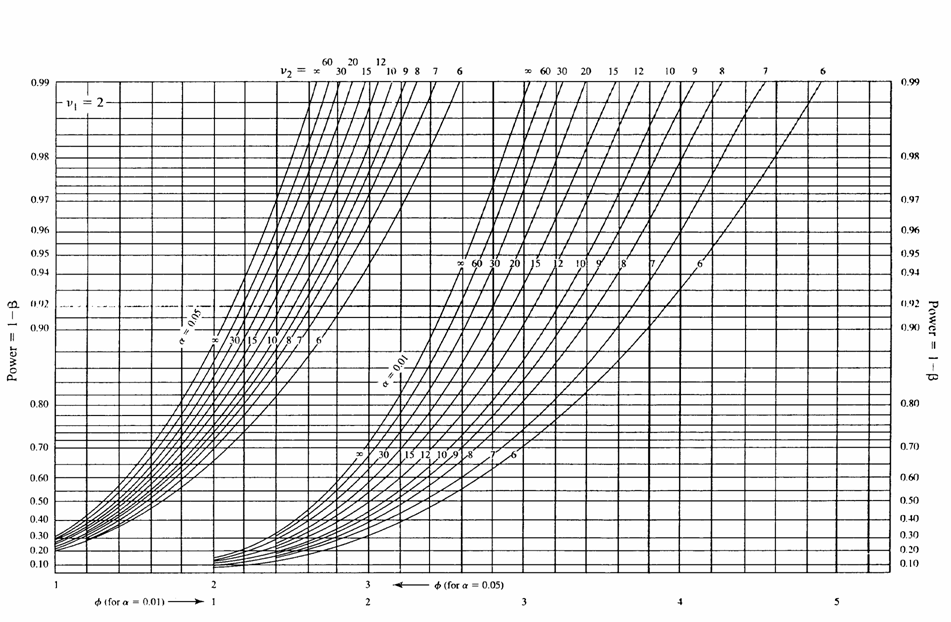
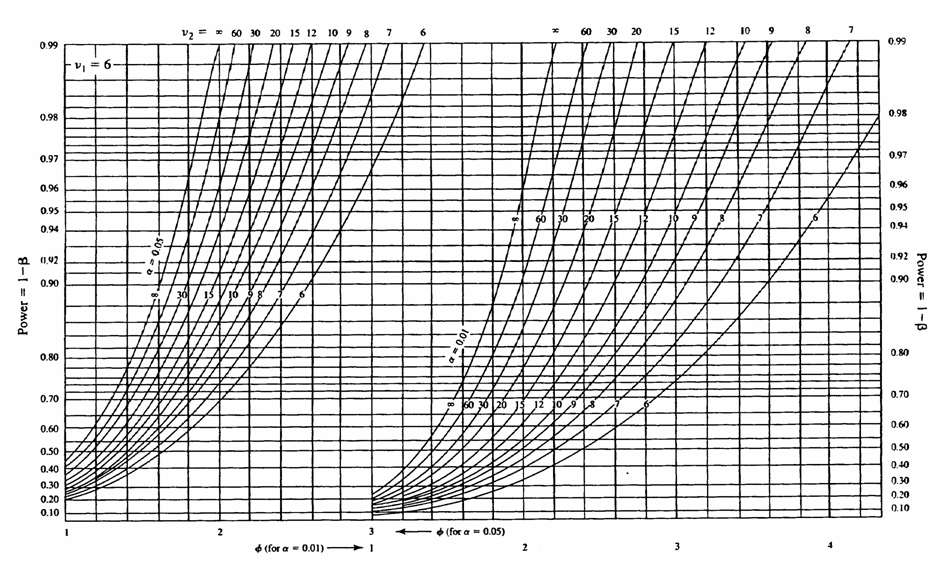
il valore di Occorre poi considerare che nell’analisi della varianza i gradi di libertà saranno - Devianza totale: df = 23 - Devianza tra media di caselle : df = 11 - Devianza tra trattamenti A df = 3 - Devianza tra blocchi B df = 2 - Devianza di interazione AB df = 6 - Devianza d’errore df = 12 Il grafico della potenza con i parametri
fornisce l’indicazione ESEMPIO 2 (POTENZA
PER I BLOCCHI) Nel disegno sperimentale presentato, valutare la potenza del
test per i blocchi per
Risposta. Se nell’ipotesi H1 si prende in considerazione la differenza reale esistente tra la media minore e la media maggiore
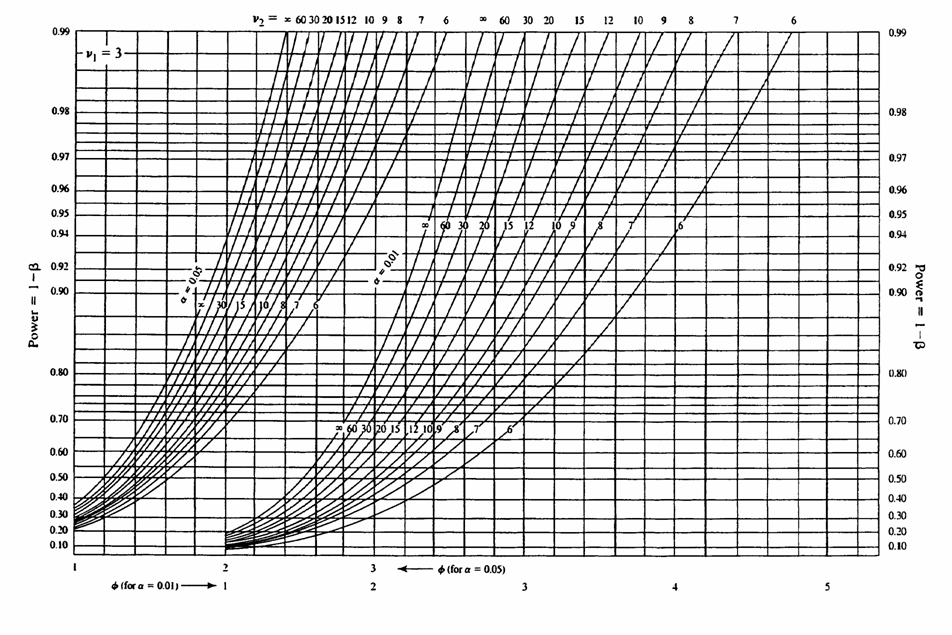
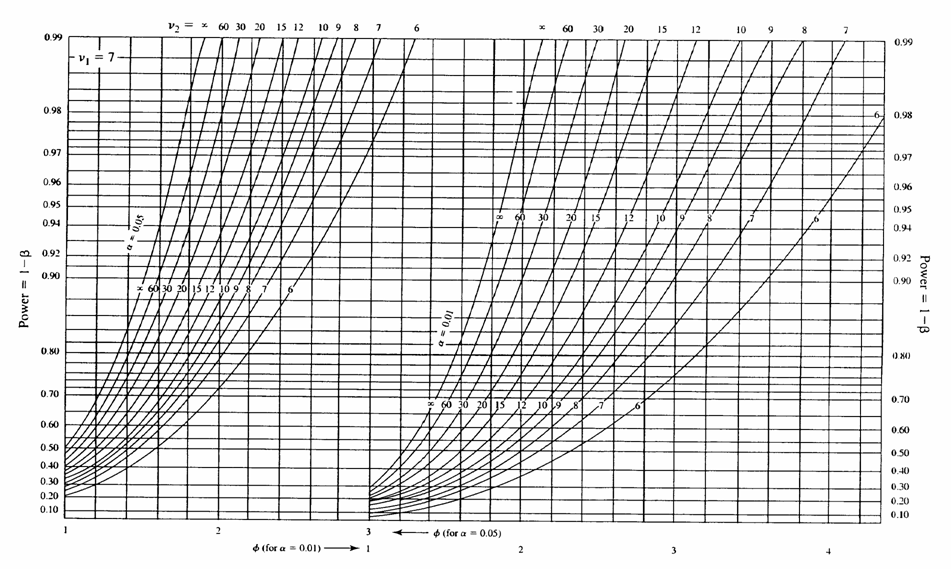
il valore di Il grafico della potenza con i parametri
fornisce
l’indicazione
ESEMPIO 3 (POTENZA
PER L’INTERAZIONE) Nel disegno sperimentale presentato, valutare la potenza del
test per l’interazione per
Risposta.
Nell’ipotesi H1 che una delle interazioni sia uguale a
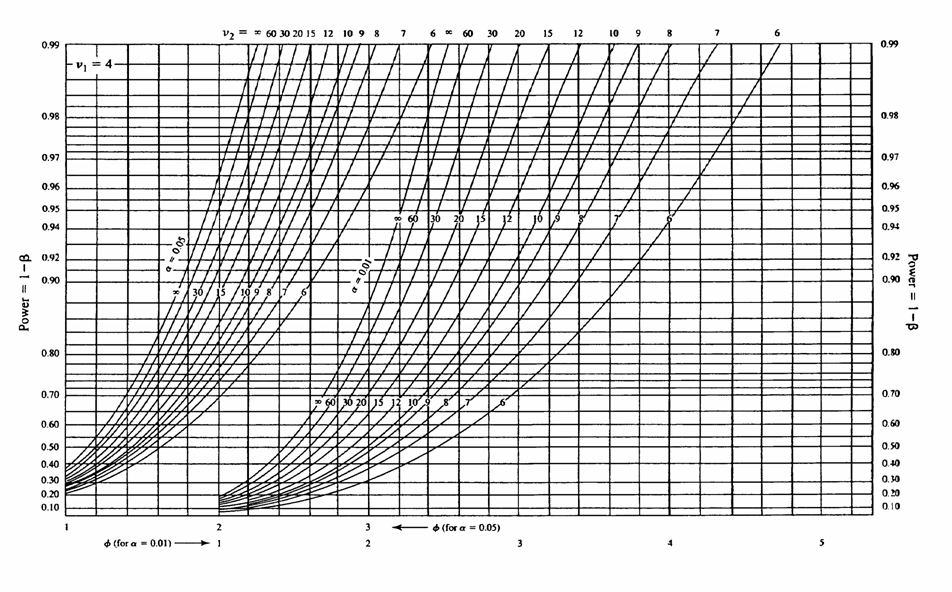
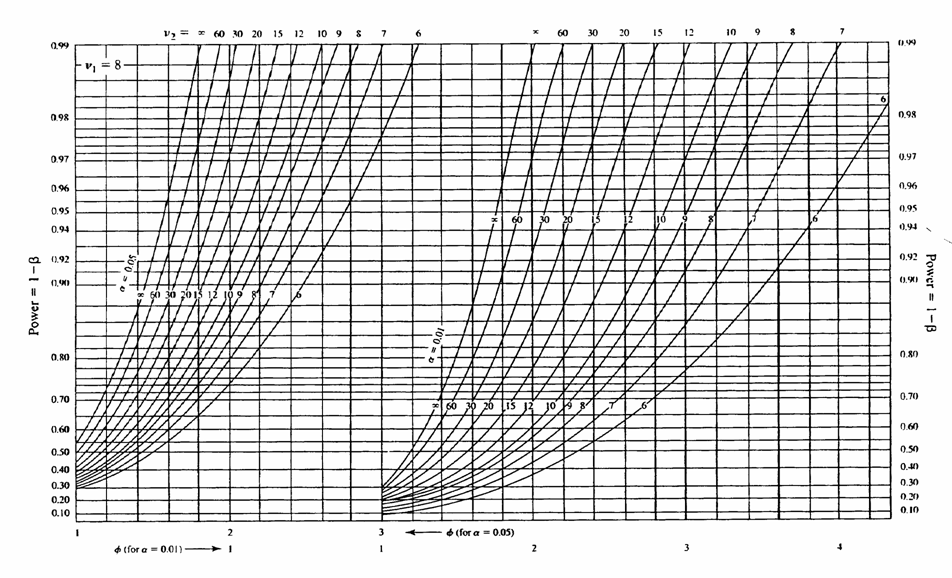
il valore di Il grafico della potenza con i parametri
fornisce
l’indicazione
E’ importante osservare che la probabilità di trovare significativo uno dei tre test che si possono condurre con i dati raccolti nel medesimo esperimento è sensibilmente differente, in quanto diversamente legate - alle dimensioni
del fattore in esame, per il calcolo del valore di - alle dimensioni
dei gradi di libertà, per individuare nel grafico il valore di
| ||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | ||||||||||||||||||||||||||||||||||||||