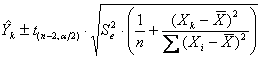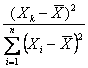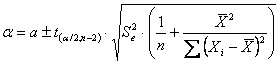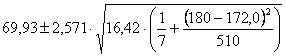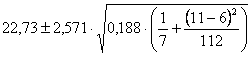|
LA REGRESSIONE LINEARE SEMPLICE
16.11. INTERVALLO DI CONFIDENZA della retta di regressione E per un singolo
Nell’analisi della retta di regressione, oltre all’intervallo di confidenza calcolato separatamente - per il coefficiente
angolare si può porre anche il problema di stimare - l’intervallo
di confidenza del valore medio di Y stimato ( Nel paragrafo successivo, sarà discusso il caso dell’intervallo di confidenza per - un dato e quello per un gruppo di dati, aggiuntivi al campione raccolto e sul quale è stata calcolata la retta di regressione.
Nella prima parte
di questo paragrafo, è presentato l’intervallo di confidenza del valore Nella seconda
parte, sarà discusso il caso in cui il calcolo è effettuato per ogni valore - l’intervallo di confidenza della retta (infatti è la stima dell’intervallo di ogni punto collocato sulla retta). Pertanto, in esso - sono considerati
congiuntamente gli effetti dell’intervallo del coefficiente angolare
Il valore medio
di
Più rapidamente,
conoscendo i valori medi
ESEMPIO 1.
Calcolare il valore medio
Risposta. Con
per un altezza
di
- con la prima formula si ricava
- e con la seconda
ottenendo sempre
L’intervallo di
confidenza di questo valore medio o valore atteso
dove - - - - - e
rappresenta l’errore
standard di
In questa formula, che mostra i fattori utilizzati nella stima, risulta con evidenza come ognuno influisca sull'ampiezza dell'intervallo di confidenza della retta. Per una data probabilità P (1-a), l’ampiezza dell’intervallo 1 - aumenta al
crescere della varianza d'errore 2 - diminuisce
all'aumentare del numero 3 - diminuisce al
crescere della devianza della variabile 4 - varia in
funzione della dimensione di
E’ importante sottolineare in particolare questa ultima (quarta) caratteristica. Il valore
è detto valore
di leva (leverage) dell’osservazione Significa che, a differenza di quanto succede per l’intervallo del coefficiente angolare, - l'intervallo
di confidenza della retta o valore medio atteso I valori di
Un secondo
aspetto importante della formula appena riportata riguarda l’intervallo
di confidenza dell’intercetta - quando
Riprendendo il concetto di leverage, si comprende come - l’intervallo di
confidenza di a sia sempre grande, quando la media è un valore elevato: la
distanza di
ESEMPIO 2 (CALCOLO DELL’INTERVALLO PER UN PUNTO PREVISTO, CON DATI BIOLOGICI). Con i dati dell’esempio sulla regressione tra altezza e peso
sui quali sono
state calcolate il punto medio per
stimare alla probabilità a = 0.05 - il suo intervallo di confidenza.
Risposta. Dalla formula
dove, sempre ricavati dai paragrafi precedenti, t(5,0.025)
= 2,571 si ottiene che per
sono dati da
Pertanto, - il limite inferiore è - il limite superiore è
ESEMPIO 3 (CALCOLO DELL’INTERVALLO PER UN PUNTO PREVISTO, CON DATI CHIMICI). Con i dati dell’esempio su concentrazione e intensità della fluorescenza,
per i quali (nei paragrafi precedenti) sono state calcolate sia la retta
sia la sua significatività, - stimare alla
probabilità a = 0.05 l’intervallo di confidenza del valore medio
Risposta. Dapprima dalla formula della retta si ricava che per
il valore di Successivamente dalla formula
dove, sempre ricavati dai paragrafi precedenti, t(5,0.025)
= 2,571 si ottiene che per
sono dati da
Pertanto, - il limite inferiore è - il limite superiore è Ancora una volta si dimostra come, con dati chimici, si possano ottenere intervalli di confidenza molto stretti. Quindi, la stima della relazione lineare tra le due variabili è molto precisa.
Impiegando sempre i 7 dati dell'esempio sulla relazione tra peso e altezza
con le modalità
seguite negli ultimi due esempi, è stato calcolato l’intervallo di confidenza
dei 7 Si è ottenuta la tabella
In essa sono riportati - i valori medi di
- gli intervalli di confidenza (L1, L2) alla probabilità a = 0.05 e a = 0.01, per alcuni valori
di E’ possibile
osservare come gli intervalli per i valori collocati più vicino alla media - -
Quando da un campione di punti, dei quali sia stata calcolata la retta di regressione
è stimato
successivamente l’intervallo di confidenza per ogni punto - un intervallo di confidenza delle rette probabili (confidence bands)che ha forma curva, come evidenziano la tabella precedente e i due grafici successivi.
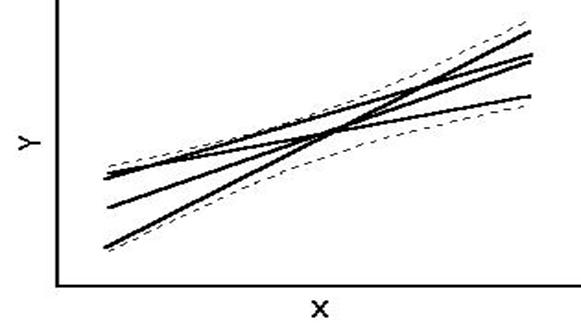
Ciò non significa
che le rette diventano curve, ma (come evidenzia la seconda figura) che l’insieme
di tutte le rette probabili al rischio - considerando
congiuntamente l’intervallo di confidenza di
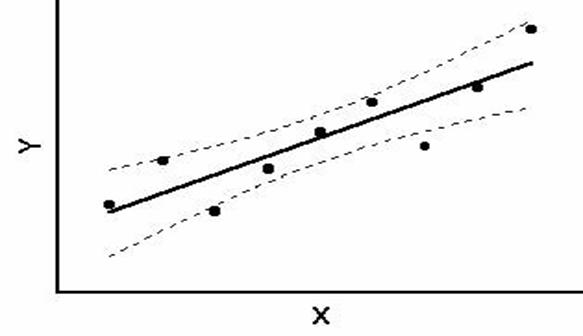
Nella prima figura, si osserva la posizione dei punti intorno alla retta e l’intervallo di confidenza (curve tratteggiate) della retta. Questo confronto dei punti con l’intervallo di confidenza spesso genera un concetto errato, che è necessario evitare per una interpretazione e un uso corretti del risultato: - l’intervallo è riferito alla retta, non ai punti. (Infatti il nome tecnico è confidence bands). Ad esempio, un
intervallo di confidenza calcolato per - assicura di avere una probabilità P del 95% di contenere la retta di regressione vera
- non di contenere il 95% dei punti campionati.
Ritornando al discorso precedente sull’intervallo di confidenza della retta e a ulteriore conferma di quanto già sottolineato, i valori di L1 e L2 riportati nella tabella e rappresentati nelle due figure evidenziano - la minore
dispersione del valore medio di - che le rette non
passano più per il baricentro
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||