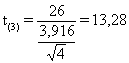ANALISI DELLA VARIANZA a piu’ criteri di classificazione

 

 

11.2.  confronto tra Analisi della varianza a due criteri e test t DI STUDENT per 2 campioni dipendenti

 

 

Quando si confrontano le medie di due soli trattamenti applicati agli stessi soggetti, quindi con valori riportati in una tabella con 2 trattamenti ed n blocchi, l'analisi della varianza a due criteri di classificazione fornisce i medesimi risultati del test t di Student per 2 campioni dipendenti, in riferimento al fattore principale.

Un esempio permette di confrontare in modo didatticamente semplice e quindi di comprendere sia le due metodologie sia i risultati relativi.

 

Durante una giornata lavorativa (Giorno I), in una stazione di rilevamento sono state misurate le quantità di inquinamento dell'aria in 4 ore differenti; durante il successivo giorno festivo (Giorno II), sono state ripetute le misure alle stesse ore.

La tabella riporta i valori rilevati nei due giorni alla stessa ora:

 

 

 

Esiste una differenza significativa nel tasso medio d’inquinamento tra i due giorni?

 

Risposta.  Con i dati del quesito, è possibile utilizzare il test t di Student per 2 campioni dipendenti per verificare l’ipotesi nulla

H₀:  d = 0

 contro l’ipotesi alternativa bilaterale

H₁:  d ¹ 0

 

Il metodo del test t di Student per 2 campioni dipendenti richiede che dapprima si calcoli la colonna delle differenze

 

 

 

 sulle quali applicare le operazioni richieste

 dalla formula

t_(n-1) =

 

Per una corretta comprensione del metodo, è importante evidenziare le due conseguenze determinate dall’uso delle differenze al posto dei valori rilevati:

- i dati utilizzati nei calcoli sono resi indipendenti da quelli originari;

- la varianza delle differenze, che possono essere viste come somma delle variazioni casuali delle coppie di dati quando l’ipotesi nulla è vera, è uguale alla somma delle varianze delle due serie di dati originali.

 

Dopo aver calcolato la media delle differenze

 si stima la devianza

 e da essa la varianza delle differenze

 e la loro deviazione standard

Il valore di t con 3 gdl

 risulta uguale a 13,28.

 

Dalle tavole del t di Student per una distribuzione a due code con 3 gdl si ricava

-          per a = 0.01, t = 5,841

-          per a = 0.005, t = 7,453

-          per a = 0.001, t = 12,941

Di conseguenza, si rifiuta l’ipotesi nulla con probabilità P< 0.001.

 

Con l'analisi della varianza a due criteri di classificazione, le ipotesi considerano

- sia il confronto tra le medie dei due giorni con ipotesi nulla

H₀:  m_I = m_II

 e ipotesi alternativa bilaterale

H₁:  m_I ¹ m_II

 

- sia quello tra le medie delle 4 rilevazioni orarie con ipotesi nulla

H₀ :   m₆ = m₁₀ = m₁₄ = m₁₈

 e ipotesi alternativa

H₁:  non tutte le 4 m dei blocchi sono tra loro uguali.

 

Dalle due serie di dati appaiati si calcolano i totali e le medie, sia quelle parziali che quella generale

 

 

 

La devianza totale con 7 gdl, calcolata come somma degli scarti al quadrato di ogni valore rispetto alla media totale,

 risulta uguale a 3362.

 

La devianza tra giorni ha 1 gdl ed è

 uguale a 1352.

 

La devianza tra ore ha  3 gdl e risulta

 uguale a 1987.

 

La devianza d'errore con 3 gdl  [7 - (1+3)]  ed ottenuta per differenza

 risulta uguale a 23.

 

Devianze e gdl possono essere riportati in tabella

 

 

 

Da essi sono stimate le 3 varianze necessarie ai due test F.

1) Per la differenza tra giorni si calcola un test F

 con gdl 1 e 3, che risulta uguale a 176,36.

Si può rifiutare l’ipotesi nulla alla stessa probabilità P < 0.001.

 

2) Per verificare la differenza tra ore si calcola

 un altro test F

 con gdl 3 e 3, che risulta uguale a 86,40.

Anche in questo caso si rifiuta l’ipotesi nulla, con probabilità P < 0.01 (valore critico uguale a 29,46).

 

Il confronto effettuato serve soprattutto per dimostrare che con 2 campioni test t e test F non solo permettono la stessa inferenza, ma forniscono anche risultati identici.

Il valore di F che permette il confronto tra le medie dei due giorni  fornisce una probabilità identica a quella del test t che verifica l’uguaglianza delle due medie giornaliere; ovviamente, coincidono anche i gdl che per il test F sono 1 e 3 e per il test t sono 3.

Infatti, sulla base della relazione

 si è ottenuto

 

Corrispondono anche i valori critici per la stessa probabilità. Infatti, come dimostrazione elementare e come caso di tutti i valori tabulati,

-          per t e per la prima colonna dei valori tabulati per F,

 è semplice verificare che per la probabilità a = 0.01 e gdl = 3 i cui valori critici sono rispettivamente

-  5,841 per il test t

-  34,12 per il test F

 esiste la stessa relazione